Филимонова Л. Н., к.ф.-м.н. Соколюк Л. Н., к.ф.-м.н. Болдырева О.Ю.

Тюменский филиал Института теоретической и прикладной механики им. С.А. Христиановича СО РАН, г.Тюмень, Россия

Циклическое заводнение кругового пласта с учётом расстановки скважин.

В работе была рассмотрена модель плоскорадиальной фильтрации реагента в слоисто-неоднородном пласте, насыщенной однофазной вязкой ньютоновской жидкостью. Слоисто-неоднородный пласт состоит из высокопроницаемого и низкопроницаемого слоя, с перетоками пластовой жидкости между ними. Исследовалось влияние периодического изменения дебита либо давления на скважине на перетоки в каждой точке рассматриваемой области. Ранее были проведены различные исследования нестационарного (циклического) заводнения, аналитические модели двухслойного пласта в плоском одномерном случае были представлены и проанализированы в работах[1,2]. В этих работах рассматривается также изменение водонасыщенностей в пропластках при перетоках жидкости между ними.

Обозначим и соответственно толщины и проницаемости высокопроницаемого и низкопроницаемого пропластков, p_i – давление жидкости в i-м слое, S_i – водонасыщенность i-го слоя, f_вi, f_нi – фазовые проницаемости слоев, b_в, b_н - коэффициенты сжимаемости для воды и нефти, q_в, q_н - удельные межслойные перетоки воды и нефти.

Таким образом, система уравнений, описывающая фильтрацию воды и нефти в двухслойном пласте, имеет вид[1]:

,

, (1)

, .

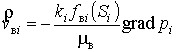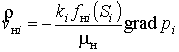Для того чтобы получить аналитическое решение системы уравнений (1) примем следующие допущения [1,2]: между высоко- и низкопроницаемым пропластками есть гидродинамическая связь; давление между слоями выравнивается мгновенно (p₁ = p₂ = p); пористости высоко- и низкопроницаемого пропластков равны (m₁ = m₂ = m);

плотности, вязкости и сжимаемости воды и нефти равны между собой (r_в = r_н = r, m_в = m_н = m, b_в = b_н = b); зависимость фазовых проницаемостей f_вi = f_в, f_нi = f_н от водонасыщенностей S_i является линейной.

При указанных допущениях система уравнений (1) может быть преобразована к следующему уравнению относительно давления:

, (2)

где , .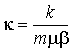

Тогда величина суммарных межслойных перетоков воды и нефти q = q_в + q_н выражается через давление следующим образом:

. (3)

Введем на плоскости полярную систему координат (r,j), граница пласта G является окружностью радиуса R, расстояние от скважины до центра окружности равно r_*, полярная ось проходит через центр окружности. На границе пласта G давление считаем равным нулю.

При периодических изменениях дебита либо давления на скважинах происходят периодические колебания во всем пласте. Поэтому решение будем искать в виде суммы стационарного p_st и нестационарного решений p¢:

.

Считаем, что p¢ гармонически зависит от времени:

. (4)

Рассмотрим следующие условия на границе пласта и на скважине:

1) ,

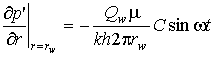2а) или 2б) . (5)

Здесь - стационарные значения давления и расхода на скважине, C - безразмерная амплитуда колебаний, p_* - характерное давление, в качестве которого удобно выбрать p_* = p_w, если на скважине задано переменное давление (условие 2а) или 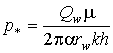, , 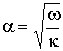если задан переменный дебит (условие 2б).

Тогда определение p¢ сведется к нахождению решения следующей системы уравнений

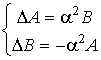(6)

с граничными условиями:

1) , (7)

2а) или 2б) .

Здесь штрих означает дифференцирование по указанному безразмерному аргументу ar.

Общее решение системы уравнений имеет вид:

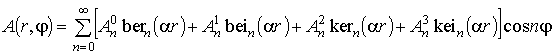, (8)

,

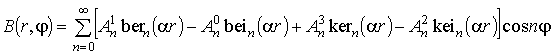где ber_n, bei_n, ker_n, kei_n - функции Кельвина[3], - произвольные постоянные.

На рис.1 показано рассчитанное поле средних по времени амплитуд перетоков жидкости между низко- и высокопроницаемым пропластками.

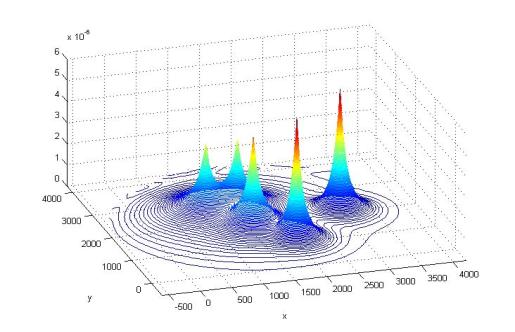
Рис.1 Межслойные перетоки воды и нефти в круговом пласте.

Таким образом, в результате выполненного исследования получено решение, определяющее межслойные перетоки воды и нефти в каждой точке рассматриваемой области.

Литература:

1. Шарбатова И.Н., Сургучев М.Л. Циклическое воздействие на неоднородные пласты. М.: Недра, 1988, 121с.

2. Горбунов А.Т., Мыхтарянц С.А., Сафронов В.И., Сургучев М.Л., Цынкова О.Э., Шарбатова И.Н. Циклическое заводнение нефтяных пластов. М.: ВНИИОЭНГ, 1977, 65с.

3. Абрамовиц, Стиган. Справочник по специальным функциям.