Технические науки 3.Отраслевое машиностроение.

Бельмас І.В., Бобильова І.Т., Соколянський І.Ю.

Дніпродзержинський державний технічний університет. Україна

ЗАЛЕЖНІСТЬ МІЦНОСТІ ГУМОТРОСОВОГО ТЯГОВОГО ОРГАНУ НОРІЇ ВІД ПОРИВІВ ТРОСІВ

Питаннями міцності гумотросових канатів та стрічок присвячено ряд робіт [1, 2]. В них розглянуті питання впливу поривів тросів в одному перерізі тягового органу зі значною кількістю тросів. В тяговому органу норії отвори розташовують в декількох перерізах. Визначення напруженого стану тягового органу з урахуванням отворів, які штучно ушкоджують троси – актуальна задача.

Кількість тросів позначимо М. Крок їх розташування - h, товщина тягового органу – t, в ньому ушкоджено по декілька довільних тросів в J перерізах. Площинами, що проходять через пориви, поділимо тяговий орган на J +1 частин. вісь х спрямуємо вздовж тягового органу. Визначимо розподіл внутрішніх сил поміж тросами тягового органу навантаженого силою розтягу Р.

Відстані поміж перерізами розташування розривів тросів позначимо l_j. Об’єднаємо номери ушкоджених тросів у (L) множин k^(j). Переміщення тросів та внутрішні сили, що в них виникають, позначимо u_і та p_і. Індекс і вказує номер тросу, до якого відноситься змінна. Сформулюємо граничні умови та умови сумісності деформування частин:

а) в перерізі х=0 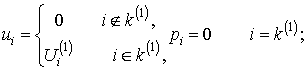(1)

б) в перерізах х=l_j.

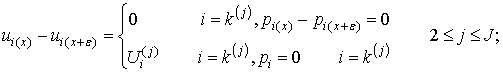(2)

в) коли , (3)

де ε – мала величина; - величини зазорів, що утворюються поміж кінцями розірваних тросів, при цьому внутрішні сили розтягу тросів в перерізах розривів дорівнюють нулю.

Задовольняючи, умовам рівноваги тросів, розподіл переміщень та внутрішніх сил розтягу тросів приймемо у формі сум рішень [3].

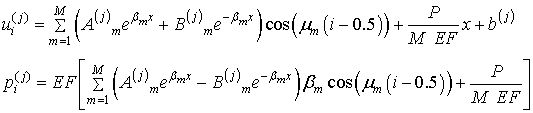, (4)

де - сталі інтегрування; EF - приведена жорсткість троса на розтяг; : ; G - приведений модуль пружності матеріалу еластичної оболонки тягового органу.

Відповідно до умови сумісності деформування тросів канату в суміжних ділянках (2), функції переміщення тросів в перерізах х=0 та х= l_j мають розриви неперервності. Відповідно вони повинні задовольняти наступним виразам

. (5)

де 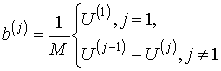, - невідомі сталі, що дорівнюють величині зазору який утворюється поміж кінцями троса в місці його розриву.

Залежності ( 4, 5), умови (1 - 3) дозволяють знайти невідомі сталі. Так для випадку J=2 вони мають наступний вигляд:

, ,

, .

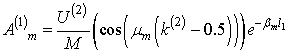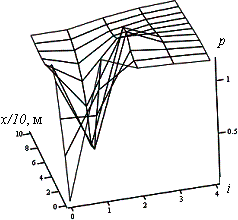
Для канату на основі тросів діаметром 4мм з ушкодженим крайнім та суміжним з ним тросом в перерізах, розташованих на відстані l=0,35м, визначено напружений стан, зумовлений середнім одиничним навантаженням на трос, (рис. 1 ). На графіку показаний розподіл сил поміж тросами.

З наведеного графіка видно, що напружений стан тягового органу змінюється локально. Мінімальні значення сил дорівнюють нулю в перерізах розриву тросів. В суміжних тросах діють максимальні сили, значення яких залежить від величини відстані поміж перерізами поривів тросів та від їх кількості (рис. 2).

Рисунок 1 Розподіл поміж тросами і зусиль розтягу Р вздовж тягового органу х

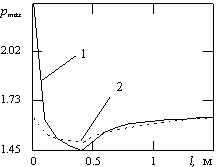
Рисунок 2 Залежність максимальних навантажень тросів рmax від відстані між перерізами ушкоджень тросів l : 1 – ушкоджені два суміжних троси; 2 - ушкоджено крайній трос

Крива 1 відтворює закон зміни максимальних внутрішніх зусиль розтягу тросів у разі поривів двох суміжних крайніх тросів. З рисунку видно, що коли l=0 (обидва ушкодження тросів розташовані в одному перерізі) максимальне зусилля р_max =2,3. Зростання відстані поміж поривами до величини м веде до зменшення значення р_max. Подальше зростання відстані веде до зростання максимального зусилля розтягу тросів до величини 1,63, що відповідає зусиллю в сусідньому тросі при ушкоджені лише одного крайнього тросу. Мінімальне значення залежності, описаної кривою 1, становить 1,45. Залежність (1) на рисунку 2 розривна функція. На ділянці м (ліва частина кривої), максимальні зусилля реалізуються в третьому з краю тросі в перерізі розриву другого. Права частина кривої (ділянка м) описує зміну зусиль в другому тросі в перерізі розриву першого.

Крива 2 – показує характер залежності максимальних внутрішніх зусиль розтягу тросів від відстані поміж двома його розривами суцільності. Як і крива 1 вона має мінімум, розташований поміж двома максимумами, величини яких дорівнюють 1,63 та відповідають випадку одиночного пориву лише крайнього тросу.

Виконані дослідження показують залежність напружено-деформованого стану від кількості тросів, якщо їх кількість не перевищує 10. При зростанні кількості тросів до 10 максимальні внутрішні сили розтягу тросів зменшуються. Таке зменшення сягає 10% від значень зусиль, отриманих в розглянутому випадку. Наявність мінімумів значень найбільших внутрішніх сил розтягу тросів в тяговому органі надає значні можливості впливу на характер напружено-деформованого стану плоского тягового органу. Так, наприклад, у разі пориву троса можна зменшити навантаження на суміжний найбільш навантажений трос на 14% шляхом вибору кроку встановлення ковшів та змінною відстанню між отворами для їх кріплення.

Напружений стан плоского тягового органу у разі пориву троса змінюється локально. По ширині внутрішні зусилля розтягу змінюються практично у суміжних тросах незалежно від конструкції тягового органу. При незначній кількості тросів в канаті максимальні коефіцієнти концентрації навантажень тросів залежать від кількості тросів в канаті, як при одному так і при двох поривах крайнього троса. Отримані результати мають використовуватися під час проектування підйомних машин та ліфтів з плоскими тяговими органами.

Література

1. Бельмас И.В. Основы теории и расчета резинотросовой конвейерной ленты с учетом его пространственной формы. - Дис. докт. наук: 05.05.06, 01.02.06. -Днепропетровск, ИГТМ, 1993.-312 с.

2.Панченко Е.В. Определение расчетных нагрузок в витках многослойной намотки резинотросового каната. Дис. канд. техн. наук. 05.02.09 – Днепропетровск, НГУ, 2007. - 206с.

3. Танцура Г.І. Модель конвеєрної стрічки з не суцільною прокладкою. Математичне моделювання. Науковий журнал. №5. - 2000. - С. 45-47.