Технические науки 3.Отраслевое машиностроение.
Колосов
Д.Л., Танцура Г.І., Ковтуновський О.С.
Національний гірничий університет, Дніпродзержинський
державний технічний університет. Україна
НДС ОБОЛОНКИ ГУМОТРОСОВОГО СТРІЧКИ
КОНВЕЄРА ПРИБИРАННЯ СТРУЖКИ НАВАНТАЖЕНОЇ
ДОТИЧНИМИ СИЛАМИ
Гумотросові стрічки
широко використовуються в машинобудуванні. Вони мають композитну побудову. До їх складу входять троси запресовані в
гумову оболонку. На ділянці взаємодії такого органу з приводним барабаном
тягове зусилля передається тросам через гумову оболонку. Її напружено-деформований стан (НДС) суттєво
впливає на міцність та безпеку експлуатації машини. Питання взаємодії плоского тягового органу з барабаном
розглядалося в роботах [ 1, 2, 3]. У вказаних роботах не досліджувався
вплив його конструкції на розподіл напружень в гумовій оболонці на ділянці
взаємодії з приводним барабаном.
Розглянемо
тяговий орган з мінімальною кількістю
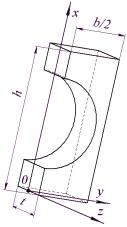
тросів – з одним тросом. На рисунку 1 показаний ескіз половинки гумової оболонки тягового органу, що має один трос. Будемо вважати, що по площині ![]() тяговий орган
закріплений нерухомо. На ньому ширину позначено літерою b, товщину - h, довжину вирізаного зразка - t
, діаметр троса – d. Побудувати розв’язок для елементу такої
складної форми. Спростимо задачу. Знехтуємо наявністю тросів. Розглянемо зразок
призматичної форми розмірами
тяговий орган
закріплений нерухомо. На ньому ширину позначено літерою b, товщину - h, довжину вирізаного зразка - t
, діаметр троса – d. Побудувати розв’язок для елементу такої
складної форми. Спростимо задачу. Знехтуємо наявністю тросів. Розглянемо зразок
призматичної форми розмірами ![]() . Зразок будемо вважати виконаним з матеріалу оболонки канату
– гуми.
. Зразок будемо вважати виконаним з матеріалу оболонки канату
– гуми.
Будемо
вважати, що у вказаного зразка точки
поверхонь в розташовані в площинах ![]() , що відповідають формі перерізу тросів переміщуються
синхронно в напрямку осі х.
, що відповідають формі перерізу тросів переміщуються
синхронно в напрямку осі х.
Будемо
вважати, що канат з барабаном взаємодіє по
поверхні ![]() . По цій поверхні
переміщень канату відносно
барабана не повинно бути.
. По цій поверхні
переміщень канату відносно
барабана не повинно бути.
![]() . (1)
. (1)
На поверхню ![]() не діють зовнішні
сили тому
не діють зовнішні
сили тому
![]() 0,
0, ![]() (2)
(2)
Граничні умови для поверхні ![]()
![]()
![]()
![]() (3)
(3)
По поверхні ![]() .
.
![]() .
.![]()
![]() .
.
По поверхням ![]() не повинні діяти
дотичні напруження, тому мають виконуватися умови
не повинні діяти
дотичні напруження, тому мають виконуватися умови
![]() . (4)
. (4)
До того мають бути реалізовані умови рівності переміщень усіх точок, що
відповідають місцю розташування троса та відсутності тиску на гуму розташовану
поміж тросами
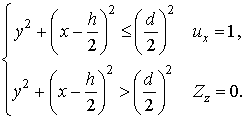 (5)
(5)
В наведених
граничних умовах переміщення позначені літерою u, напрямок переміщення індексом, що відповідає осі координат.
Дотичні напруження позначені ![]() та
та ![]() . Нормальні напруження позначені двома однаковими літерами,
що збігаються з відповідним напрямом, наприклад
. Нормальні напруження позначені двома однаковими літерами,
що збігаються з відповідним напрямом, наприклад ![]() .
.
Переміщення
та напруження визначаються залежностями через бігармонічну функцію φ.
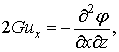
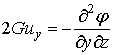 ,
, 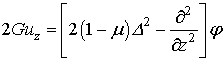 ,
,
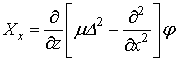 ,
, 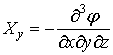 ,
, 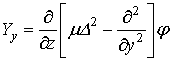 ,
,
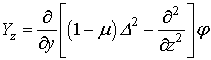 , (6)
, (6)
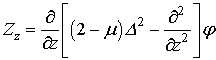 ,
,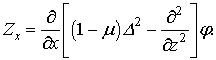
де 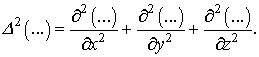
Функцію приймемо наступного
вигляду
![]() , (7)
, (7)
де An,m, Dn,m , Nn,m, Mn,m Cn,m – довільні сталі; 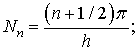
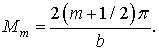 ;
; ![]() .
.
Значення сталих Dn,m знайдемо з умови відсутності дотичних напружень по
границям зразку ![]() . Вказана умова
виконується коли
. Вказана умова
виконується коли
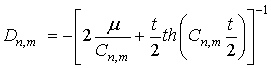 . (8)
. (8)
Переміщення
вздовж осі z та нормальний тиск мають
вигляд
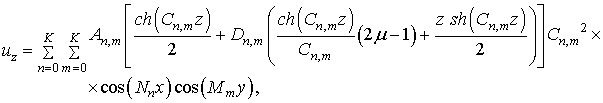 (9)
(9)
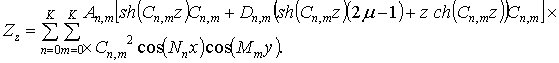 (10)
(10)
Шукані напруження зсуву в
площинах паралельних площині тертя
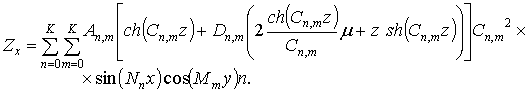 (11)
(11)
Граничні умови (5) змішані.
Відповідно до прийнятого рішення (11) в перерізі ![]() нормальні напруження
нормальні напруження ![]() Тому замість (5) приймемо умову
Тому замість (5) приймемо умову
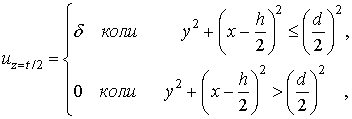 (12)
(12)
де δ - величина зсуву частини перерізу гумового зразку, що відповідає
місцю розташування троса в гумовій оболонці тросу.
Шуканий
розподіл дотичних напружень будемо мати в перерізі ![]() . Для цього розкладемо залежність (12) в подвійний ряд.
. Для цього розкладемо залежність (12) в подвійний ряд.
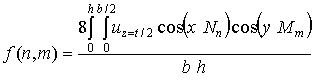 .
(13)
.
(13)
З урахуванням
(11) та (12) визначимо невідомі сталі
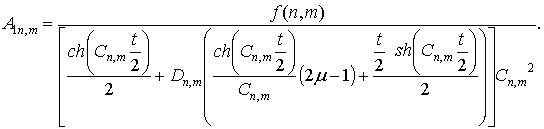
Визначені
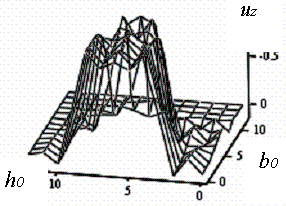
невідомі сталі забезпечують заданий характер деформування зразка uz по поверхням ![]() . Розподіл для зразка висотою t=1/4d, з тросом одиничного діаметру (d=1)переміщень показано на
рисунку 2.
. Розподіл для зразка висотою t=1/4d, з тросом одиничного діаметру (d=1)переміщень показано на
рисунку 2.
Застосовані
на рисунках параметри h0 та b0 визначаються за
залежностями 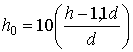 та
та 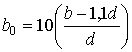 .
.
|
Рисунок 1 – Симетрична
частину гумової оболонки відрізку канту |
Рисунок 2 – Графік
переміщень uz поверхні зразка в площинах |
Відзначимо,
що і в перерізі z=0 графік переміщень практично
збігається з графіком зображеним на рисунку 2. Прийнята форма рішення та задані
значення елементів масивів ![]() та
та ![]() не забезпечують
повного виконання умов (1) (2) та (3).
Так в умовах (1) для поверхні
не забезпечують
повного виконання умов (1) (2) та (3).
Так в умовах (1) для поверхні ![]() умова
умова ![]() - виконується лише
коли z=0. На поверхні
- виконується лише
коли z=0. На поверхні ![]() (2) умова
(2) умова ![]() 0 виконується також лише коли z=0. Для
поверхні
0 виконується також лише коли z=0. Для
поверхні ![]() .
. ![]() - виконується лише коли z=0. З урахуванням
останнього, далі розглядали
напружено-деформований стан зразка в площині z=0.
- виконується лише коли z=0. З урахуванням
останнього, далі розглядали
напружено-деформований стан зразка в площині z=0.
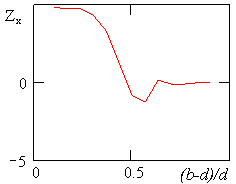
З
використанням залежності (11) визначили
дотичні напруження в площині
дотичній до поверхні троса з боку нерухомого приєднання гумового зразка – в перерізі ![]() (рис. 3).
(рис. 3).
З графіку
видно, що дотичні напруження змінюються по ширині зразка та відрізняються від
нуля лише навпроти троса. Максимальних значень набувають при мінімальній
відстані від поверхні тросу до нерухомо закріпленої поверхні гумової оболонки.
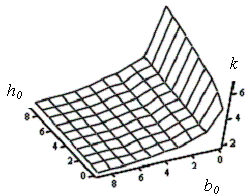
Характер розподілу напружень залежить і від геометричних параметрів канату. При
розрахунках міцності деталей машин конструктори користуються коефіцієнтом
концентрації напружень. Він дорівнює відношенню максимальних напружень до
середніх. На рисунку 4 показана залежність коефіцієнта концентрації напружень
від параметрів гумотросової стрічки.
|
Рисунок 3 – Графік розподілу
дотичних напружень вздовж осі у у
відносних координатах |
Рисунок 4 - Залежність
коефіцієнта концентрації напружень
k від параметрів канату h0 та b0 |
Незначна
різниця в характерах НДС гумової оболонки гумотросової конвеєрної стрічки в
різних площинах ![]() та
та ![]() свідчить про їх
відповідність напружено-деформованому
стану зразка з тросом.
свідчить про їх
відповідність напружено-деформованому
стану зразка з тросом.
Отримана
залежність коефіцієнта концентрації напружень від параметрів канату дозволяє
врахувати розподіл напружень в гумі при
проектуванні підйомно-транспортних машин з гумотросовим тяговим органом
чим підвищити безпеку експлуатації
таких машин.
Література
1. Бельмас І.В., Колосов Д.Л., Бобильова І.Т. Врахування дотичних напружень при
автоматичному конструюванні ступінчастого канату // Стальные канаты. Сб.
научных трудов. – Одесса. – 2009. – №7. – С. 147-152.
2. Білоус О.І., Колосов Д.Л. Напружений стан гумової оболонки стрічки на барабані
конвеєра подачі шихти в доменну піч // Металлургическая и
горнорудная промышленность. – 2010. – №4(262). – С. 113-114.
3. Блохин
С.Е., Колосов Д.Л., Колосов А.Л. Напряженно-деформированное состояние плоского
резинотросового тягового органа на барабане // Вісник Дніпропетровського
національного університету залізничного транспорту ім. акад. В. Лазаряна. –
2009. – №30. – С. 88-91.