К

К.т.н. Тихонов В.А.

Институт машиноведения Российской академии наук, Москва, Россия

Способы расчета слоистых резинометаллических виброизоляторов

Предлагаются варианты расчета тонкослойных резинометаллических элементов – ТРМЭ, как упругих виброизолирующих элементов, двумя способами: аналитическим и численным методами решения в разных задачах. Линейные задачи статики и динамики решаются, чаще всего, полученными для тонких слоев резины асимптотическими аналитическими решениями. Нелинейные задачи, такие как устойчивость слоистого пакета при сжатии, косослой, большие деформации – с применением модифицированного метода решения краевой задачи. Методики использованы при проектировании конструкций патрубков трубопроводов высокого давления [1] .

Для анализа виброзащиты машин, оборудования, патрубков чаще всего ставится общая задача оценки переходных частотных характеристик матрицы жесткости по соотношению структурной механики между обобщенными силами и смещениями через матрицу жесткости. При оценках виброизолирующих свойств патрубка наибольший интерес представляют переходная жесткость и коэффициент передачи.

Задача определения матрицы жесткости патрубка сводится к расчету наряженного состояния при сжатии, изгибе и сдвиге, а также действии внутреннего избыточного давления в кольцевом элементе, который, в свою очередь, после процедуры интегрирования по высоте тонкого резинового слоя приводятся к краевой задаче Гельмгольца. Задачи проектирования патрубка и расчета элементов рассмотрены в работах [1-3].

Решения относительно гидростатического давления s в тонком резиновом слое находятся из уравнения Гельмгольца на примере кольца:

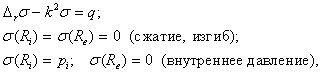
где G и K – модули сдвига и объемного сжатия резины;

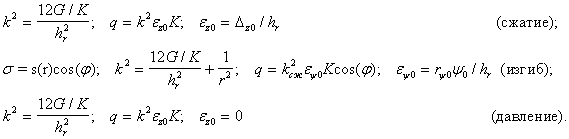
Напряжения и перемещения выражаются через гидростатическое давление. Для линейных задач получены аналитические решения уравнения в виде функций гидростатического давления. В реальных условиях приходится решать геометрически и физически нелинейные задачи, для которых предлагается использовать электронные средства пакета MathCad , в котором предусмотрено численное решение нелинейных дифференциальных уравнений. Краевая задача приводится к задаче Коши. Дифференциальное уравнение второго порядка приводится к системе уравнений первого порядка и строится вектор-функция у: , компоненты которой определяются так:

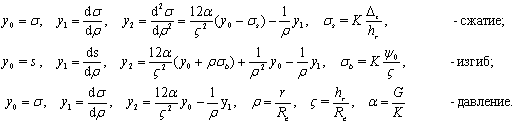
Относительно символьной вектор-функции D (r,y)= {y₁ , y₂} решается краевая задача, которая с помощью функций: приводится к решению задачи Коши методом Рунге-Кутта: _{, где}_x₁_,_x₂_{– граничные точки интервала
интегрирования – для кольца:}_r_i₌_Ri_/_Re _и_r_e_{= 1;}_v_{– вектор начального приближения; с помощью функции}_score_{задается нулевое граничное условие}_y₀_{– 0 на давление в задачах сжатия и изгиба и равное избыточному давлению}_y₀_–_pi_{при его наличии, тогда приходится менять порядок краевых точек}_x₂_,_x₁_{местами, в том числе и
в функции}_sbval₍_v_,1,1,_r_,_n_,_D₎_{, которая путем
разделения интервала на}_n_{точек определяет недостающее второе граничное условие на производную}_d_s_{(в задаче это – вектор) на другом конце
интервала. Решение задачи Коши с помощью функции}_rkfixed_{содержится в матрице}_Z_{, где первый столбец –
точки разбиения интервала по ширине кольца:}_r_k_,_k_=1,...,_n_{, второй – значения
функции}_s₍_r_{) в этих точках, третий
– значения производной}_d_s_/_d_r_{, которое используется
для расчета касательных напряжений. При проектировании кольцевого элемента решаются
нелинейные задачи с косослоем и поперечной устойчивостью слоистого пакета.}

Неравномерность резинового слоя по толщине как технологическое несовершенство, выраженное в непараллельности жестких тарелей и фланцев, задается начальным взаимным поворотом на угол тарелей и фланцев – функцией толщины от полярных координат в виде:

где – номинальное значение толщины резинового слоя постоянной толщины (предыдущий вариант), – полярная координата точки, соответствующей минимальной толщине слоя при угловой координате изгибной деформации j =0, при этом решение при изгибе ищется в виде s = scosj. Напряженное состояние в резиновом слое определяется решением двухточечной краевой задачи:

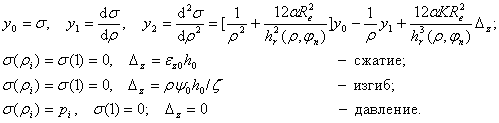
Так задача со слоями постоянной толщины приведены к системе дифференциальных уравнений, решаемых методом Рунге-Кутта. Данное представление позволяет получить решения нелинейных задач с учетом зависимостей модулей упругости резины G и K (a = G/K) от интенсивности деформаций и гидростатического давления. Иллюстрацию некоторых решений можно найти в [3]. Решена задача потери поперечной устойчивости при сжатии. Построена нелинейная кривая: нагрузка – стрела «прогиба» (максимальное смещение сдвига слоя в пакете), аналогичная нагрузочной кривой потери устойчивости сжатого стержня с начальной погибью.

Литература

1. Кирюхин А.В., Тихонов В.А., Чистяков А.Г. Вибрационные характеристики углового компенсационного патрубка с тонкослойными эластомерными элементами // Проблемы машиностроения и надежности машин. 2007, №1, С. 103-108.

2.Тихонов В.А. Расчет вибрационной жесткости сферического резинометаллического подшипника // Проблемы машиностроения и надежности машин. 2004, 6, стр. 9-14.

3.Кирюхин А.В., Тихонов В.А., Чистяков А.Г. Расчет нелинейных характеристик ТРМЭ при проектировании компенсационных патрубков. – В сб. тр. XVII Симпозиума: Динамика виброударных (сильно нелинейных) систем. «DYVIS-2012». Москва-Клин. 2012. С. 96-99.