Технические науки/6.Элекротехника и радиоэлектроника

К.т.н. Гнатов А.В., асп. Шиндерук С.А., асп. Барбашова М.В.

Харьковский национальный автомобильно-дорожный университет, Украина

Анализ процессов в индукционной индукторной системе с идентичными листовыми немагнитными металлами

Постановка проблемы. Практическая работоспособность любой индукторной системы определяется её геометрией, электрофизическими и геометрическими характеристиками отдельных элементов, а также амплитудно-временными параметрами токового импульса в их взаимосвязи [1, 2].

Индукционные индукторные системы (ИИС) впервые были предложены и описаны авторами работы [3]. Их первоначальное назначение состояло в создании сил магнитно-импульсного притяжения немагнитных металлов, а принцип действия основан на взаимодействии проводников с одинаково направленными токами (закон Ампера).

Анализ основных достижений и публикаций. Исследования электромагнитных процессов в ИИС с немагнитными вспомогательным экраном и листовой заготовкой были обобщены авторами научного издания [3]. Наиболее простой конструктивно и достаточно эффективной представляется ИИС с идентичными тонкостенными листовыми экраном и заготовкой. Геометрическая и электродинамическая симметрия такой конструкции инструмента должна обеспечить квадратичную зависимость его силовых характеристик от параметров тока, возбуждающего систему.

В работе [4, 5] авторами проведен анализ электродинамических процессов и их расчёт в ИИС с одинаковыми тонкостенными листовыми ферромагнетиками. Возникает необходимость исследовать процессы в аналогичной ИИС с неферромагнитными металлами. Это позволит разрабатывать и создавать эффективные инструменты для магнитно-импульсной обработки металлов любой физической природы.

Цель настоящего рассмотрения – расчёт и анализ электромагнитных процессов в индукционной индукторной системе с одинаковыми тонкостенными листовыми неферромагнетиками.

Электромагнитные процессы

Для анализа электромагнитных процессов примем расчётную модель в цилиндрической системе координат, показанную на рис. 1.

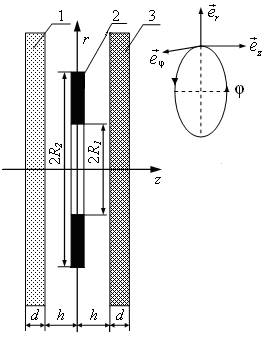
Рис. 1. Расчётная модель в цилиндрической системе координат

(направляющие орты),

1 – экран (толщина); 2 – виток (внутренний и внешний радиусы;

3 – заготовка (толщина); расстояние от витка до экрана или заготовки.

При решении примем допущения, аналогичные публикациям [4, 5].

Уравнения Максвелла для возбуждаемых составляющих вектора электромагнитного поля, преобразованных по Лапласу с учётом нулевых начальных условий, имеют вид [3–5]:

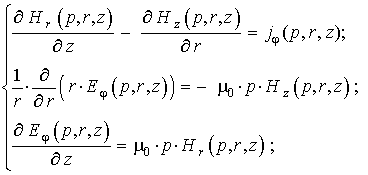(1)

где р – параметр преобразования Лапласа;

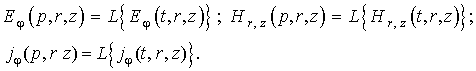
Опуская математические операции по интегрированию составленных уравнений Максвелла, выполненных аналогично работам [2–5] в конечном итоге получаем

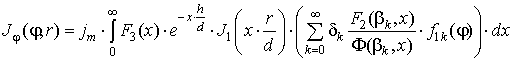, (2)

где ,

,

,

.

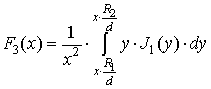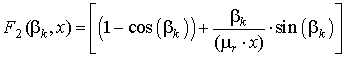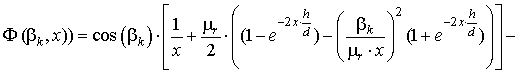
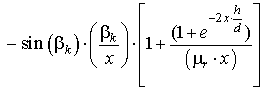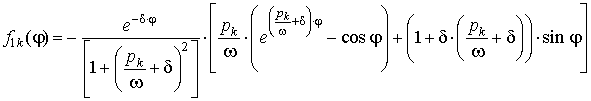. (3)

Особыми точками функции комплексного переменного являются простые, отличные от нуля полюсы :

, (4)

где характерное время диффузии поля в металл листовой заготовки с удельной электропроводностью и магнитной проницаемостью – .

С помощью полученных аналитических выражений для индуцированных токов, проведём численные оценки характеристик процессов в рассмотренной ИИС.

Для проведения конкретных вычислений следует задать её параметры.

1) Геометрия типичной экспериментальной конструкции: м, м, м.

2) Листовые вспомогательный экран и обрабатываемый объект: м, металл – образцы из немагнитной стали ( 1 ⁄ (Ом·м)).

С практической точки зрения наибольший интерес представляют вычисления для различных значений рабочих частот. Эти оценки дадут представления о соотношении эффектов отталкивания и притяжения в зависимости от временных характеристик действующих полей в их связи с электрофизическими параметрами металлов обрабатываемых объектов – проводящих листовых заготовок.

Графические иллюстрации расчётных зависимостей от безразмерных фазы – j = w t и радиальной координаты – r/R₂ представлены ниже для частот f= 250 кГц (рис. 2) и f = 2 кГц (рис. 3).

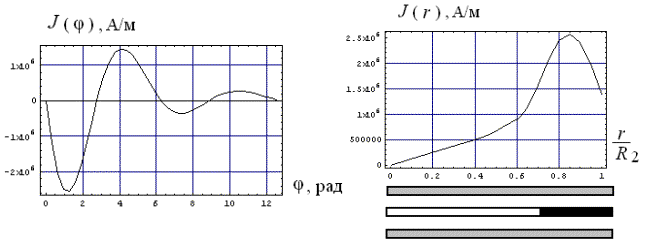
а) б)

Рис. 2. Линейная плотность индуцированного тока в немагнитной стали при частоте f = 250 кГц

а), в) – фазовая зависимость в контуре радиуса ;

б), г) – радиальное распределение для временного максимума.

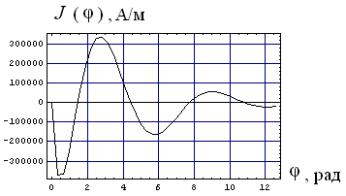
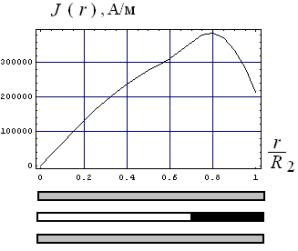
а) б)

Рис. 3. Линейная плотность индуцированного тока в немагнитной стали при частоте f = 2 кГц

а) фазовая зависимость в контуре радиуса ;

б) радиальное распределение для временного максимума.

Анализ графиков для немагнитной стали (рис. 2, 3) приводит к следующим выводам.

· При высоких частотах действующих полей (f = 250 кГц, рис. 2) фазовая зависимость индуцированного тока практически повторяет ток индуктора (с точностью до знака). Радиальное распределение в значительной мере сосредоточено вблизи витка.

· Рабочие частоты ~ 2 кГц (рис. 3) уже можно считать достаточно низкими с точки зрения соответствия временных форм индуцированных токов производной тока индуктора. В радиальном направлении индуцированные токи занимают почти всю внутреннюю область под витком индуктора.

· Таким образом, в рассмотренной индукционной индукторной системе для рабочих частот f = 2 кГц и ниже временной режим действующих полей в соответствии с геометрическими и электрофизическими характеристиками листовых металлов приближается к идеализации «прозрачных» проводников. Лоренцевы силы отталкивания на немагнитные стали должны становиться несущественными.

Если говорить об эффективности индукционной индукторной системы как инструмента притяжения, то следует учитывать не только изменение временных форм амплитуд индуцированных токов, но и снижение их амплитуд. В диапазоне частот кГц амплитуды падают от ~ 2,2 МА/м до 0,1МА/м. То есть, более чем в ~ 20 раз. Но при понижении рабочих частот вместе с отталкиванием падает и сила притяжения, пропорциональная квадрату токов. По-видимому, при создании реальных конструкций инструментов индукционного типа следует ориентироваться на наибольшее значение рабочей частоты, для которой силы Лоренцевого отталкивания становятся малозначимыми.

Выводы

Основные результаты проведенного рассмотрения сводятся к следующим положениям.

1. Проведен расчёт и анализ электромагнитных процессов в индукционной индукторной системе с одинаковыми тонкостенными листовыми неферромагнетиками.

2. Проведенные численные оценки показали, что при рабочих частотах порядка 2 кГц можно считать, что электромагнитные процессы протекают в низкочастотном режиме действующих полей.

3. При выборе рабочей частоты следует учесть, что при понижении рабочих частот вместе с отталкиванием падает и сила притяжения, которая, в свою очередь, пропорциональна квадрату токов.

Литература

1. Белый И.В., Фертик С.М., Хименко Л.Т. Справочник по магнитно-импульсной обработке металлов. – Харьков: Вища школа. 1977. – 190 с.

2. Батыгин Ю. В. Магнитно-импульсное притяжение/отталкивание тонкостенных листовых ферромагнетиков / Ю. В. Батыгин, А. В. Гнатов // Электричество. – М., 2012. – № 8.– С. 58–65.

3. Туренко А. Н. Импульсные магнитные поля для прогрессивных технологий. Том 3. Теория и эксперимент притяжения тонкостенных металлов импульсными магнитными полями: монография / А. Н. Туренко, Ю. В. Батыгин, А. В. Гнатов. – Х. : ХНАДУ, 2009 – 240 с.

4. Гнатов А. В. Универсальный инструмент бесконтактной магнитно-импульсной рихтовки – симметричная индукционная индукторная система / А. В. Гнатов, С. А. Шиндерук, Д. П. Петренко // Вісник НТУ ”ХПІ”. Зб. наук. праць. – 2013. – № 51. – С. 106–116.

5. Гнатов А. В. Силы Лоренца в универсальном инструменте магнитно-импульсной рихтовки. / А. В. Гнатов, С. А. Шиндерук // Вісник СевНТУ. Серія: Машиноприладобудування та транспорт: зб. наук пр. – Севастополь, 2013.– Вип. 143. – С. 240 – 243.