Технические науки/8. Обработка материалов в машиностроении

К.т.н. Реченко Д.С., Ильин Е.И., Леонтьева Е.В., Матвеева М.Г.

Омский государственный технический университет, Россия

Моделирование напряженно-деформационного состояния в твердосплавном режущем инструменте при затачивании

Анализ технологий изготовления твердосплавных режущих элементов инструмента для обработки жаропрочных и титановых материалов показал, что при затачивании режущего инструмента важное значение имеет качество лезвия, сведение к минимуму дефектов, возникающих на нем. Кроме того, существенным фактором, влияющим на стойкость инструмента, является уровень остаточных напряжений на поверхности и в приповерхностных слоях на режущем лезвии, после затачивания. Качественные режущие поверхности и лезвие инструмента оказывают значительное влияние на процесс резания, износ режущего инструмента во время работы и качество обработанных поверхностей изделий [3, 7]. Особо актуальна эта проблема при затачивании твердых сплавов, где наблюдается хрупкое разрушение под действием температуры и сил резания.

Согласно ранее проведенным исследованиям, экспериментально определенные силы резания при различных методах алмазного шлифования твердого сплава составляют:

- традиционное алмазное затачивание F=200…300 Н;

- алмазное затачивание с непрерывной электрохимической правкой поверхности алмазного круга F=80…100 Н;

- электрохимическое алмазное затачивание F=55…70 Н;

- комбинированный метод, сочетающий электрохимическое алмазное затачивание с одновременной непрерывной электрохимической правкой поверхности алмазного круга F=30…40 Н;

- высокоскоростной метод затачивания F=5…30 Н.

Следовательно, последние три метода могут быть рекомендованы для качественного формообразования твердосплавного лезвия режущих элементов. Однако требуются комплексное исследование качества затачивания инструмента для обработки жаропрочных и титановых материалов этими методами.

В связи с этим, требует изучения напряжённо-деформированное состояние режущей кромки и поверхностей вблизи её при затачивании инструмента с геометрией для обработки жаропрочных и титановых материалов, традиционными методами и высокоскоростным шлифованием.

Постановка задачи и методика моделирования

Режущие элементы твердосплавного инструмента имеют сложную трехмерную геометрическую конфигурацию. Из ранее проведенных исследований [1, 2, 4, 5, 7] известно, что разрушение материала режущих элементов, как правило, происходит вдоль режущего лезвия на расстояниях, не превышающих 0,3 мм.

Для моделирования процесса затачивания твердосплавного режущего элемента принята схема обработки и действующие при этом динамические составляющие процесса, соответствующие торцевому шлифованию.

Затачиваемый режущий элемент, имеющий форму пластины, с углом заострения β закреплен неподвижно в специальной оснастке. Шлифовальный круг (в данном случае чашечный конический) вращается вокруг своей оси с постоянной скоростью V м/с. Кроме того, шлифовальный круг поступательно движется в сторону затачиваемого режущего элемента с постоянной скоростью, равной величине продольной подачи S_пр м/мин. В процессе затачивания с поверхности режущего элемента снимается слой материала равный величине поперечной подачи S_поп мм/дв.ход.

В результате кинематического воздействия шлифовального инструмента на обрабатываемую заготовку в зоне резания возникают технологические силы и температура, которые достаточно просто измерить с высокой точностью.

Примем некоторые допущения для оценки напряжённо-деформированного состояния режущей кромки:

· Материал режущего элемента считается однородный сплошной и анизотропный.

· В процессе обработки он испытывает незначительные деформации.

· Разрушение материала считается хрупким, т.е. при превышении предела прочности происходит отслаивание материала.

· Технологические силы, действующие на режущий элемент со стороны шлифовального инструмента, распределены равномерно по поверхности затачивания.

· Предполагается, что режущая кромка является абсолютно острой (радиус округления равен нулю).

· Все зерна шлифовального круга имеют одинаковый размер и обеспечивают равномерное распределение сил.

Упрощенно процесс шлифования рассматривают как результат воздействия на обрабатываемую поверхность движущегося алмазного зерна. В действительности поверхность абразивного круга представляет собой распределенные по объему зерна, размеры которых находятся в узком диапазоне отклонений и сами зерна геометрически отличаются друг от друга. В результате каждое зерно круга снимает малую часть материала, существенное влияние оказывает рабочий диаметр круга и скорость сдвига в месте обработки. Допущение об однородной поверхности круга может приводить к завышенным значениям параметра поврежденности вблизи области шлифования. Тем не менее, распределение дефектов в режущем клине должно быть подобно реализующемуся на практике. Уровень остаточных напряжений и степень поврежденности твердых материалов в зоне шлифования зависят от большого количества технологических и физических факторов. Определение рационального сочетания параметров процесса затачивания зависит не только от физико-механических свойств обрабатываемого материала, но и конкретных геометрических размеров изделия. Выберем в качестве объекта исследования клин определенной ширины и длины с углом заострения β=90°, и углом в плане 90° в зависимости от условий обработки и сочетания инструментального и обрабатываемого материала.

Условные варианты образцов обрабатываемой пластины принятой в модели представлены на рисунке 1.

а) б) в)

Рис. 1. Условные варианты обрабатываемой пластины: а) без стружколома;

б) с фаской; в) со стружколомом

Практический интерес представляет изучение закономерностей формирования напряженно-деформированного состояния, область распределения деформаций и перемещений в элементах режущего инструмента из твердых материалов при затачивании алмазным кругом.

Для исследования формирования напряженно-деформированного состояния в зоне затачивания пластины из сплава высокой твердости была использована математическая модель, разработанная в рамках расчетного подхода механики повреждаемых сред.

Физико-математическая модель включает уравнения сохранения массы, импульса и энергии. Определяющее уравнение напряжения принимает вид:

.

Опасной называется точка элемента системы, в которой σ_экв по одной из теорий прочности достигает наибольшего значения, и условие прочности тогда можно записать в виде:

где σ₁, σ₂, σ₃ – главные напряжения в по направлению осей x, y, z соответственно; [σ] – допустимое напряжение для принятого материала.

Сформулировать универсальный критерий равнопрочности, учитывающий всю совокупность причин, практически влияющих на прочность (тип напряженного состояния, состояние материала, характер действия на тело внешних факторов) до сих пор не удалось. Поэтому, в настоящее время при расчете на прочность используется несколько теорий прочности, взаимно дополняющих друг друга. Теории прочности, объясняющие возникновение предельного состояния разрушением, называются теориями хрупкого разрушения, а объясняющие его возникновение появлением недопустимых пластических деформаций - теориями пластичности.

В работе принята теория удельной потенциальной энергии формоизменения - энергетическая теория (теория Мизеса - Генки). Критерий равнопрочности: напряженные состояния равнопрочны по наступлению недопустимых пластических деформаций, если у них равны удельные потенциальные энергии формоизменения:

,

откуда эквивалентное напряжение для объема:

.

Под действием напряжений принятый объем деформируется, в результате каждая грань изменяет свои размеры, в направлении координатных осей и может получить угловую деформацию (Рис. 2).

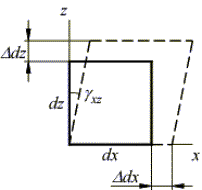
Рис. 2. Вид деформируемой грани

Таким образом, в направлении оси z элементарный размер dz грани получит относительную деформацию ε_z, а в направлении оси x элементарный размер dx изменится на величину ε_x. Угол между ребрами грани изменится на величину γ_xz. Подобные деформации получат и остальные грани элементарного объема. Тогда деформированное состояние в точке определится тензором деформаций:

,

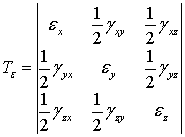где линейные деформации:

,,

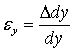и угловые деформации:

,,.

Свойства деформированного состояния аналогичны свойствам напряженного состояния, в частности, можно выделить три взаимно перпендикулярные оси, в системе которых угловые деформации отсутствуют. Главные деформации нумеруют в порядке убывания .

Для деформаций в объеме получим:

, , .

Полученные зависимости представляют собой обобщенный закон Гука в главной системе координат:

, , .

В качестве примера, исследуем систему композиционного твердого сплава марки ВК8, в состав которого входят карбиды вольфрама WC и кобальт Co. Экспериментальные данные о механических характеристиках сплавов WC-Co широко представлены в литературе [6].

Решение вычислительной модели выполнено на примере твердого сплава ВК8 с помощью конечно-разностного метода, реализованного в программе Solid Works 2012.

Для этого была построена расчетная область соответствующая обрабатываемой пластине из твердого сплава. Габаритные размеры пластины в расчетной модели были приняты равными: ширина пластины a=12 мм, длина пластины b=12мм, угол заострения β=90°, форма пластины – квадрат, радиуса при вершине – 0,5 мм. Граничные условия на поверхностях жесткого закрепления: нижняя базирующая и задняя боковая; торцевые боковые и передняя поверхности свободные поверхности, на которых были заданы граничные условия, соответствующие свободной от нагрузки поверхности. На задней передней поверхности выделена область, соответствующая участку нагружения вдоль режущей кромки инструмента, где были заданы граничные условия силовых и температурных распределнных нагрузок. Кинематические граничные условия имитировали сдвиг поверхностного слоя в результате воздействия сил резания и температуры от поверхности шлифовального круга на поверхность пластины,

Для оценки напряженно-деформированного состояния и перемещения в зоне шлифования были расчитаны изменения параметров в лагранжевых точках – точки на уголках и посередине на режущей кромке пластины. Расчетные значения интенсивности напряжений, возникающие при шлифовании с заданными параметрами распределенными по обрабатываемой поверхности получали при крайних значениях силы и температуры резания:

- для классического шлифования чашечным шлифовальным кругом усилия резания 100-300 Н, линейная скорость сдвига материала с обрабатываемой поверхности 15-45 м/с, температура в зоне шлифования 400-1000 °С.

- для высокоскоростного шлифования специальным шлифовальным кругом усилия резания 5-30 Н, линейная скорость сдвига материала с обрабатываемой поверхности 200-270 м/с, температура в зоне шлифования 200-400 °С.

Оценка напряженно-деформированного состояния в затачиваемой пластине при скорости сдвига 15-45 м/с

Таблицы 1

Тип пластины	Пластина без стружколома	Пластина с фаской	Пластина со стружколомом
	V=15-45 м/с, Т=1000 °С, F=300 Н
Распределение напряжения
Распределение перемещения
Распределение деформации
Область распределения напряжений
Параметры расчетов	σmax=25,90 МПа δ=1,14∙10^-1 мкм	σmax=24,86 МПа δ=1,07∙10^-1 мкм	σmax=25,10 МПа δ=1,31∙10^-1 мкм

Наибольший интерес, с точки зрения качества затачивания режущего лезвия и поверхностей инструмента, имеет распределение значений параметров напряжений и перемещений режущего лезвия.

Результаты исследования той же модели в условиях высокоскоростного шлифования представлены на рисунках 4.4.28…4.4.35.

Тип пластины	Пластина без стружколома	Пластина с фаской	Пластина со стружколомом
	V=200-270 м/с, Т=200 °С, F=5 Н
Распределение напряжения
Распределение перемещения
Распределение деформации
Область распределения напряжений
Параметры расчетов	σmax=3,46 МПа δ=5,07∙10^-3 мкм	σmax=3,11 МПа δ=4,68∙10^-3 мкм	σmax=3,14 МПа δ=5,42∙10^-3 мкм

Предложена физико-математическая модель процессов деформации, повреждения и разрушения твердых материалов типа WC-Co при шлифовании алмазным кругом, позволяющая проводить оценку напряженно-деформированного состояния, перемещения, деформацию и область распределения напряжений в обрабатываемой пластине. Расчетная модель реализована на примере алмазного затачивания твердосплавной пластины марки ВК8 с несколькими вариантами геометрий режущих элементов, характерной для инструмента, предназначенного для обработки жаропрочных и титановых материалов. Модель может быть адаптирована и для других высокопрочных и труднообрабатываемых материалов. Таким образом, появляется возможность оценить напряженно-деформированное состояние для различных инструментальных материалов.

Физико-математическая модель позволила выявить, что в результате взаимодействия алмазного круга с поверхностью обрабатываемой пластины в объеме пластины формируется сложное напряженно-деформированное состояние, зависящее от условий обработки. Ниже приведена таблица результатов расчета для крайних значений силы и температуры резания при классических и высокоскоростных режимах резания.

Зонами наибольшей концентрации напряжений являются участки вдоль режущей кромки пластины, где могут прослеживаться частичные разрушения твердого сплава.

При классическом затачивании (V=15-45 м/с) силы резания находятся в диапазоне 100…300 Н, температура в зоне резания составляет 400…1000 °С, поэтому при обработке пластин возникают напряжения в диапазоне: σ_max=8,72-25,90 МПа, а перемещения составляют δ=0,0388-0,114 мкм – для сплошных твердосплавных пластин; σ_max=8,34-24,86 МПа, перемещения δ=0,0364-0,107 мкм – для твердосплавных пластин с фаской и σ_max=8,45-25,10 МПа, перемещения δ=0,0445-0,131 мкм – для твердосплавных пластин со стружколомом. При повышении скорости резания до V=200-270 м/с силы резания снижаются до 5…30 Н, а температура до 200-300 °С, что позволяет снизить напряжения до: σ_max=3,46-6,14 МПа, а перемещения до δ=0,00507-0,0165 мкм – для сплошных твердосплавных пластин; σ_max=3,11-6,37 МПа, перемещения δ=0,00468-0,0153 мкм – для твердосплавных пластин с фаской и σ_max=3,14-6,41 МПа, перемещения δ=0,00542-0,0182 мкм – для твердосплавных пластин со стружколомом.

При повышении скорости резания до 200-270 м/с наблюдается снижение напряжений в 1,3…7,8 раза (в среднем в 4,6 раза), а перемещения снижаются в 0,6…23,2 раза (в среднем в 11,9 раза).

Критическими, с точки зрения начала интенсивного развития микроповреждений в приповерхностных слоях и зонах, находящихся вблизи области обработки являются условия шлифования (сила резания и температура в зоне шлифования).

Результаты моделирования процесса шлифования пластины из сплава ВК8 при линейной скорости до 45 м/с и прижимающем усилии свыше 100 Н и температуре свыше 400 °С свидетельствуют о возможности образования повреждений в объеме пластины под обрабатываемой поверхностью, что также подтверждается исследованиями других авторов.

Следовательно, для затачивания алмазными кругами лезвия режущего инструмента из инструментальных материалов группы ВК (WCCo), рекомендуется добиваться линейных скоростей на контактирующих поверхностях в пределах от 200 м/с и выше. Для достижения требуемого качества затачивания режущих поверхностей и лезвия инструмента из твердых сплавов необходимо применять методы и условия обработки, гарантирующие силы резания не превышающие 30 Н.

Литература:

1. Артамонов, Е.В. Напряженно-деформированное состояние и прочность режущих элементов инструментов / Е.В. Артамонов, И.А. Ефимович, Н.И. Смолин, М.Х. Утешев / Под ред. М.Х. Утешева. – М.: ООО «Недра:Бизнесцентр», 2001. – 199 с.: ил.

2. Бобров, В.Ф. Основы теории резания металлов / В.Ф. Бобров. – М.: Машиностроение, 1975. – 344 с.

3. Деренговский, А.Г. Напряженно-деформированное состояние линейно-упругого материала в окрестности вершины остроугольного концентратора напряжений: Дисс. ... канд. техн. наук. – Орел, 2007. – 196 с.

4. Захаренко, И.П. Алмазная заточка твердосплавного инструмента / И.П. Захаренко, А.А. Шмелев. – Киев: Наукова думка, 1978. – 218 с.

5. Лоладзе, Т.Н. Прочность и износостойкость режущего инструмента / Т.Н. Лоладзе. – М.: Машиностроение, 1982. – 320 с

6. Панов, В.С. Технология и свойства спеченных твердых сплавов и изделий из них / В.С. Панов, А.М. Чувилин. – М.: «МИСИС», 2001. – 428 с.

7. Полетика, М.Ф. Контактные нагрузки на режущих поверхностях инструмента. – М.: Машиностроение, 1969. – 148 с.: ил.