Калініна М.Ф.

Національний технічний університет України «КПІ»

АНАЛІЗ ДИНАМІКИ ТОРСІОННОГО ПІДВІСУ ВНУТРІШНЬОЇ РАМКИ ГІРОСКОПА В АКУСТИЧНОМУ ПОЛІ

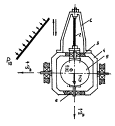
Будується розрахункова модель пружної взаємодії торсіонного підвісу внутрішньої рамки гіроскопа з проникаючим акустичним випромінюванням і з’ясовується природа виникнення додаткових похибок позиціонування (рис. 1). Під дією плоскої хвилі тиску в кожній із трьох струн генеруються хвильові процеси, які призводять до переміщень W₁ , W₂ , W₃ , їх нижніх кінців 1, 2 і 3 (рис. 1, а). За синфазного руху цих точок по дотичній до кола радіусом r, виникаюча в струнах вібрація буде слугувати появі крутильних коливань з кутовою швидкістю відносно поздовжньої осі торсіона (рис. 1, а).

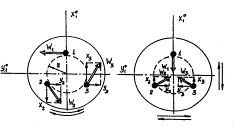
Окрім цього, коливання струн в поперечному напрямку призведуть до появи поступальних переміщень вздовж осі торсіона. Якщо переміщення нижніх точок струн будуть радіальними, тоді складові прискорень створять зворотньо-поступальний рух осі в двох взаємно-перпендикулярних напрямках (рис. 1, д). Таким чином збурений рух буде складатися з двох – поступальної вібрації вздовж осей х і у, а також крутильних коливань відносно осі внутрішньої рамки із швидкістю і відносно осі зовнішньої рамки з кутовою швидкістю (рис. 1, д). Останні все ж не викличуть систематичного дрейфу гіроскопа, а перші, коливання з кутовою швидкістю призведуть до дрейфу осі фігури.

в)

б)

а)

д)

Рис. 1. Торсіонний підвіс в акустичному полі: а) загальний вид; б) підвіс із трьох струн; в, д) – вимушені переміщення точок кріплення струн

Таким чином, збурюючий момент відповідно до теореми Резаля, призведе до прецесії вектора кінетичного моменту .

За перше наближення математичної моделі торсіона обрано хвильове рівняння

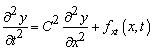, [1]

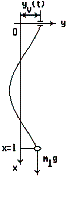де у – параметр, який характеризує поперечний рух точки струни; t – час; х – просторова координата ; – геометричний розмір; С – швидкість розповсюдження хвиль вздовж осі х; – зовнішня сила віднесена до одиниці маси струни (рис. 2).

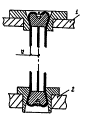
Рис. 2. Розрахункова схема для Рис. 3. Розрахункова схема малих хвильового рівняння коливань навантаженої струни

Розрахункова схема може бути наведена у формі однорідної нерозтяжної нитки з вагою на вільному кінці (рис. 3).

Для з’ясування більш тонких моментів динаміки торсіонного підвісу, струну слід розглядати як важку нитку з однією вагою на вільному кінці [2]. В цьому випадку натяг в кожній точці струни дорівнює сумі мас зосереджених під нею точок помножених на прискорення земного тяжіння g. Зовнішня сила позначається як .

Найбільш ефективною і, разом з тим, найменш трудомісткою моделлю

розрахунків слугує дробно-раціональна модель струни у вигляді сукупності зосереджених мас, які з’єднані між собою нерозтяжними нитками.

Література:

1. Аверіна Т.В. Динаміка елементів систем [Текст]: навч. посібник / Т.В. Аверіна, Н.А. Кубрак. – К.: ІЗМН, 1998. – 224 с.

2. Карачун В.В. Математична модель взаємодії акустичного випромінювання з торсіонним підвісом гіроскопа [Текст]/ В.В. Карачун, В.М. Мельник// Nowoczesnych naukowych osiagniec-2008: Materialy IV Mezinarodne vedecko-praktika konferencji, Przemysl, 1-4 lutego 2008 roku. - Str. 41-44.