Построение векторной целевой функции для
оценки риска снижения устойчивости коммерческого банка
Егоркин Е.А. (Северо-Кавказский гуманитарно-технический институт, г.
Ставрополь)
Для
оценки рискованности кредитной организации, обосновано полагая, что система
формирования и анализа ее финансовой устойчивости относится к группе задач «риск-доход», могут быть применены
многокритериальные методы оптимизации, лежащие в основе распределения объекта
исследования с учетом волантильности группы анализируемых критериев.
Учитывая,
что при оценки риска изменчивости финансовой устойчивости банка необходимо
сформировать информационный массив, позволяющий представляющий необходимые
сведения органам надзора за деятельностью банков и всем заинтересованным
потребителям о соотношении ресурсной обеспеченности, ликвидности,
эффективности, качестве активов, доходности деятельности кредитной организации и уровне риска, позволяющий
ранжировать банки по степени возрастания риска утраты ими финансовой
устойчивости. Наиболее эффективным инструментом для решений этой задачи
является векторная целевая функция (ВЦФ), лежащая в основе теории принятия
решений.
Основная
цель ВЦФ состоит в выявление объекта х0, который будет оптимален по
каждому критерию, определенного при составлении ВЦФ. Для упрощения решения
будем применять прямые методы. Таким образом, ВЦФ можно представить, как
функцию, включающую как максимизируемые или минимизируемые критерии:
Fi(x) = {F1(x), F2 (x), …. Fn(x)} (1)
![]()
![]() (2)
(2)
Выделенные критерии
оценивают различные состояния анализируемого объекта, относительно которого
принимается решение. Они должны отвечать следующим требованиям:
1.
Однородность критериев Fi(x), включенных ВЦФ, по виду экстремума, т.е. либо все
критерии являются минимизируемыми, либо максимизируемыми.
2.
Все критерии, включенные
в ВЦФ должны быть соизмеримыми, т.е. иметь одну единицу измерения.
3.
Все критерии должны быть
сопоставимыми, т.е. отражать равный
вклад локальных индикаторов в интегральную полезность данной ВЦФ.
Говоря
обобщенно, при оценке риска изменения финансовой устойчивости коммерческого
банка наибольшее значение придается
прогнозированию стабильности деятельности банка по годам и традиционными
и наиболее применяемыми показателями оценки риска является дисперсия σ2
или среднеквадратическое отклонение (СКО) σ величины ожидаемой уровня
финансовой устойчивости банка. При этом необходимо отметить, что
среднеквадратическое отклонение и
дисперсия показывают абсолютную колеблемость признака. Однако, мы считаем,
что более информативным показателем риска будет коэффициент вариации,
рассчитываемый как отношение
среднеквадратического отклонения к математическому ожиданию, что позволит сопоставить изменчивость
показателей, определенных в разных единицах измерения. И чем больше полученное значение вариации, тем сильнее
изменчивость, что говорит о том, что этот критерий является
минимизируемым.
Величина ожидаемого уровня финансовой устойчивости
коммерческого банка является случайной величиной, приобретающей некоторые
значения, при неизвестном распределении вероятностей. Мы полагаем, что
свойственный исследуемому объекту х характер значений уровня финансовой
устойчивости в рамках анализируемого
временного ряда сохраняет свои особенности, и переносит их на следующие годы в рамках
рассматриваемого планового периода. Из этого следует, что с некоторой погрешностью можно
определить величину ожидаемого уровня финансовой устойчивости банка Уi = Уi(x) , достигаемого при
соответствующих значениях вероятностей Pi = Pi(x), ![]()
![]() .
.
Таким образом, ожидаемый уровень финансовой устойчивости
коммерческого банка рассчитывается в виде математического ожидания
![]() (4)
(4)
и представляет собой максимизирующий критерий. Среднеквадратическое отклонение в свою
очередь рассчитывается: 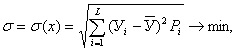 (5)
(5)
получаем коэффициент вариации, как ранее было отмечено, являющийся
минимизируемым критерием степени риска:
![]() (6)
(6)
Учитывая сложность применения
при оценке риска изменения уровня финансовой устойчивости классическое
распределение риск-доходность, определяемое с помощью β-коэффициента, то,
на наш взгляд, целесообразно использовать для расчета риска коэффициента ассиметрии
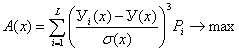 (7)
(7)
и коэффициента эксцесса,
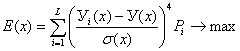 (8)
(8)
которые являются макимизирующими критериями.
Экономический смысл данных коэффициентов при рассчитанном
математическом ожидании У состоит в том, что рост показателя асимметрии говорит о наличии благоприятных тенденций в
развитии объекта, когда растет вероятность
усиления уровня финансовой устойчивости конкретного банка, превышающих величину
математического ожидания (3). Некоторые ученые
эту тенденцию обозначают как
«правый хвост». И наоборот, его снижение свидетельствует о неблагоприятных
тенденциях, когда повышается вероятность снижения стабильности в работе
кредитной организации, т.е. интегральный уровень ее финансовой устойчивости
меньше величины математического
ожидания У. Соответственно,
при уменьшении коэффициента (5.6)
формируется «левый хвост», точки которого образуются снижающимися
значениями величины интегрального показателя финансовой устойчивости
банка.
Экономический смысл коэффициента эксцесса
состоит в том, что повышение данного показателя свидетельствует о усилении
стабильности в деятельности
экономической системы, в частности коммерческого банка, т.е.
увеличивается вероятность получения значение уровня финансовой устойчивости банка,
близкого к среднему и снижение вероятности «рассеивания» значений в большую или
меньшую сторону. Соответственно снижение показателя говорит о том, что плотности
вероятностей случайной величины уровня финансовой устойчивости будет не таким
«остро
вершинным», а скорее приплюснутым или растянутым. Следовательно, это свойство можно
определить, как увеличение вероятности получить либо низкий уровень, либо высокий
уровень финансовой устойчивости, что говорит о высокой колеблемости показателя,
предполагая при этом симметричное распределение вероятностей.
Не менее эффективным
является применение финансовых коэффициентов при оценке риска колеблемости
финансовой устойчивости банка. Во второй главе диссертационного исследования,
мы выявили наиболее показательные и результативные показатели, определяющие
финансовую устойчивость коммерческого банка.
С учетом требований к выбору критериев и построению ВЦФ, мы сформировали
комплекс показателей и выделили их векторную направленность:
1) коэффициент
достаточности капитала: ![]() ,
,
2) коэффициент
соотношения высоколиквидных активов и привлеченных средств: ![]() ,
,
3) коэффициент
стабильности ресурсной базы: 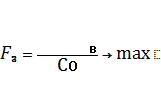 ,
,
4) коэффициент
эффективности использования активов:  ,
,
5) коэффициент качества
ссудной задолженности: ![]() ,
,
6) коэффициент
рентабельности активов: ,
7) коэффициент чистой
процентной маржи:  ,
,
8) коэффициент чистого стабильного финансирования: ![]() .
.
9)
коэффициент вариации ожидаемого уровня финансовой устойчивости - ![]() .
.
10)
Коэффициент асимметрии - 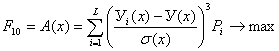 .
.
11) коэффициент эксцесса ожидаемого уровня финансового потенциала
- 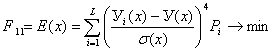 .
.
С
учетом необходимости выполнения требования однородности критериев, то всем
экстремумам ВЦФ следует быть либо максимизируемыми, либо минимизируемыми.
Выделяют два основных пути решения этой задачи. Первый направлен на определение
обратного значения исходному показателю путем перевода первоначальное значение
через степень (-1). Второй метод направлен на определение некоторой константы,
позволяющей заменить минимизируемый
критерий на максимизируемый критерий Fυ’(x)= Cυ - Fυ(x). Каждый из
этих подходов используется в зависимости от конкретного содержания Fυ(x).
В результате мы получили 11 максимизируемых
критериев (т.е. n = 11), составляющих ВЦФ (1). Таким
образом, искомая векторная целевая функция, состоящая только из максимизируемых
экстремумов.
Распределение банков относительно риска снижения
финансовой устойчивости осуществляется в соответствии с принципом Парето. В соответствии с
этим принципом устойчивые объекты могут
принадлежать Паретовскому множеству ![]() ; элементы подмножества (Х\
; элементы подмножества (Х\![]() )- доминирующие относительно критериев ВЦФ и
поэтому не могут рассматриваться в качестве потенциально финансово устойчивых
объектов. Поэтому ранжирование банков осуществляется в соответствии с
убыванием финансовой устойчивости объектов множества Х по
совокупности значений критериев.Это распределение осуществляется с
помощью прямых методов теории принятия решений с применением обобщенного решающего правила (ОРП),
сформулированного в исследованиях Е.В. Поповой и состоящего из трех решающих правил
(РП): MAXMIN, MAXSUM, и «расстояние до
идеальной точки».
)- доминирующие относительно критериев ВЦФ и
поэтому не могут рассматриваться в качестве потенциально финансово устойчивых
объектов. Поэтому ранжирование банков осуществляется в соответствии с
убыванием финансовой устойчивости объектов множества Х по
совокупности значений критериев.Это распределение осуществляется с
помощью прямых методов теории принятия решений с применением обобщенного решающего правила (ОРП),
сформулированного в исследованиях Е.В. Поповой и состоящего из трех решающих правил
(РП): MAXMIN, MAXSUM, и «расстояние до
идеальной точки».