ссс

Экономические науки/8. Математические методы в экономике

К.ф.-м.н. Зинченко А.Б., Усачев Д.Э.

Южный федеральный университет. Россия

Условия непустоты С-ядра кооперативной игры в форме характеристической функции

Анализ кооперативной игры в форме характеристической функции , где и , обычно начинается с проверки непустоты ее С-ядра

являющегося основной концепцией решения теории неантагонистических игр. Если характеристическая функция задана таблично, то проблема сводится к проверке совместности линейной системы, определяющей С-ядро, или решению задачи

, (1)

где - множество собственных коалиций. Если - оптимальное решение задачи (1), то тогда и только тогда, когда

Для вывода критерия существования С-ядра, выраженного через характеристическую функцию, используется задача

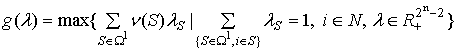, (2)

двойственная к (1). Допустимая область задачи (2)полностью определяется количеством игроков и является выпуклым многогранником в. С-ядро игры существует тогда и только тогда, когда выполняется условие сбалансированности Бондаревой-Шепли [1]-[2]

, ,

эквивалентное условию

, ,

где - множество крайних точек многогранника_.Игра с непустым С-ядром, называется сбалансированной. Каждый вектор содержит не менее нулевых компонент, поэтому используют сокращенную запись, указывая только значения положительных компонент и соответствующие им коалиции. Семейство коалиций назовем минимальным сбалансированным множеством (м.с.м.), если существует такая вершина , что для , и для . Вектор положительных компонент вершины назовем весом м.с.м. . Невырожденной вершине соответствует невырожденное м.с.м. , состоящее из коалиций (₎. Однородное м.с.м. состоит из коалиций одинаковой мощности (_,₎. Булева матрица , где - характеристический вектор коалиции , является матрицей м.с.м. _. Матрица однородного м.с.м. содержит одинаковое количество единиц в каждой строке. Любое м.с.м. имеет дополнительное м.с.м. , вес которого вычисляется по формуле

, .

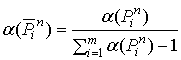Очевидно, . Поэтому дополнительное к минимальное сбалансированное множество можно назвать двойственным. Семейство всех м.с.м. обозначим через . Условие сбалансированности игры можно записать в виде

, . (3)

Цель данной статьи – описание метода генерирования достаточных условий существования С-ядра игры с помощью минимальных сбалансированных множеств, а также их сравнение с известными достаточными условиями.

Минимальные сбалансированные множества , соответствующие целочисленным вершинам многогранника , являются разбиениями множества (, , ). Вес каждого разбиения - единичный вектор . Количество неравенств системы (3), резко возрастают при увеличении . Некоторые из них определяют критерии непустоты других множеств, использующихся в кооперативной теории. Например, неравенство , соответствующее м.с.м. ,выделяет класс игр с непустым множеством дележей

Двойственное к м.с.м. выделяет класс игр с непустым множеством двойственных дележей

где - вклад игрока в максимальную коалицию. Набор м.с.м.: , и , , выделяет класс игр с непустым -ядром .

Для краткости будем называть неравенства из условия сбалансированности (3) балансирующими неравенствами, неравенства , где , - усиленными балансирующими неравенствами, а также отождествлять игру с ее характеристической функцией и, без ограничения общности, рассматривать неотрицательные игры , .

Очевидно, игра имеет непустое -ядро тогда и только тогда, когда совместна система

,, , (4)

отличающаяся от системы, определяющей -ядро тем, что уравнение

(5)

заменено неравенством . Запишем (4) в виде

, (6)

где , . Первыми строками матрицы являются характеристические векторы коалиций. Последняя строка соответствует максимальной коалиции. Пусть - базис матрицы . Систему (6) можно привести к виду , , где - подматрица матрицы , состоящая из строк, не вошедших в базис. Система уравнений определяют базисное решение . Если

, (7)

то - допустимые решение системы (6).

Пусть – невырожденное м.с.м., тогда его матрица является базисом _.Допустимое базисное решение системы (6) может не удовлетворять уравнению (5), т.е. не принадлежать С-ядру. Однако с помощью можно определить множество дележей, содержащихся в С-ядре. Векторы , , где

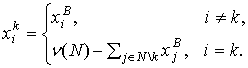
принадлежат С-ядру. Следовательно, (7) является достаточным условием сбалансированности, соответствующим базису . Из выпуклости вытекает .

Пример 1. Невырожденному однородному м.с.м. соответствует единичная базисная матрица и базисное решение . Условие (7) имеет вид

,, , , (8)

что эквивалентно

,, .

Эта система состоит из одного балансирующего неравенства (соответствующего м.с.м. ) и усиленных балансирующих неравенств (соответствующих , , ). Векторы , , где

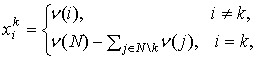
совпадают с крайними точками , , множества дележей. Из и следует, что условие (8) выделяет конус сбалансированных игр, С-ядром которых является множество дележей. Такие игры называются -симплексными [3]. Множество -симплексных игр содержит аддитивные игры.

Выведем теперь достаточное условие, соответствующе м.с.м. , двойственному к .

Утверждение 1. Пусть. Условия

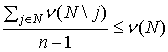, (9)

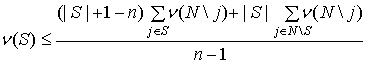, , , (10)

определяют подмножество сбалансированных игр, содержащее класс двойственно -симплексных игр.

Доказательство. Базис , соответствующий м.с.м. , обратная матрица и базисное решение определяются формулами

, .

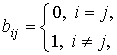
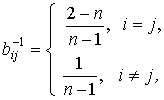
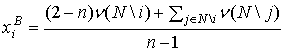Подставляя в (7) и учитывая равенство

получаем (9)-(10). Прибавляя к левой и правой части неравенств из (10) , получаем более наглядную форму системы (9)-(10)

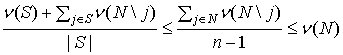, , . (11)

Двойственно -симплексная игра [3], определяется (9) и условием

, . (12)

Обозначим , или

Согласно (9), . Умножая последнее неравенство на , получаем

Из этого неравенства вытекает

или . Если выполняется (12), то , что эквивалентно левой части условия (11). Получили, что любая двойственно -симплексная игра удовлетворяет (11). ÿ

Неравенство (9) является балансирующим неравенством, соответствующим м.с.м. . Зафиксируем коалицию , и рассмотрим м.с.м. с весом . Ему соответствует балансирующее неравенство

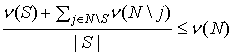. (13)

Из (9), (11) и (13) следует, что полученное в утверждении 1 достаточное условие непустоты С-ядра состоит из одного балансирующего неравенства и усиленных балансирующих неравенств.

Характеризующим свойством двойственно -симплексной игры является совпадение С-ядра с множеством двойственных дележей. Из доказанного выше следует, что множества игр, удовлетворяющих условиям (7), полученным с помощью пары двойственных м.с.м. и , имеют "двойственные" свойства. В первом случае выделяется класс -симплексных игр, во втором – множество, содержащее двойственно -симплексной игры.

Следующий пример показывает, что описанное в утверждении 1 множество сбалансированных игр не совпадает с множеством двойственно -симплексных игр.

Пример 2. Игра трех лиц

, , , , , ,

не является -симплексной, т.к. ее С-ядро

не совпадает с множеством дележей

Игра не является двойственно-симплексной, т.к. С-ядро не совпадает с множеством двойственных дележей

Тем не менее, игра удовлетворяет условию (11), которое для состоит из четырех неравенств

, ,

Вектор не принадлежит С-ядру, но определяет подмножество его элементов , где , , .

В следующих двух утверждениях выведены достаточные условия, соответствующие, базисам, полученным из и заменой одной из строк строкой .

Утверждение 2. Пусть и . Условие

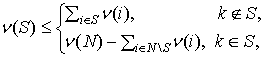
, (14)

выделяет подмножество сбалансированных игр, содержащее -симплексные игры для таких коалиций , что .

Доказательство. Рассмотрим базис

Обратная матрица, совпадающая с, и базисное решение определяются формулами

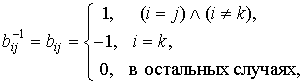
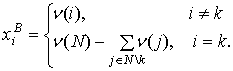
Подставив в (7) получаем (14). -симплекной [5] называется игра , в которой крайние точки С-ядра совпадают с крайними точками , , множества дележей. Так как вектор является крайней точкой С-ядра и совпадает с , то все -симплекные игры () удовлетворяют (14). ÿ

Неравенства из (14) являются балансирующими (для ) и усиленными балансирующими (для ).

Утверждение 3. Пусть и . Условие

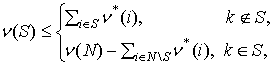
, (15)

выделяет подмножество сбалансированных игр, содержащее двойственно -симплексные игр для таких коалиций , что .

Доказательство. Рассмотрим базис

Базисная матрица, обратная матрица и базисное решение определяются формулами

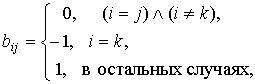
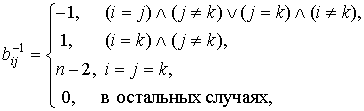
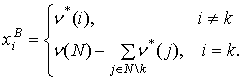
Подставив в (7) получаем (15). Двойственно -симплекной [5] называется игра , в которой крайние точки С-ядра совпадают с крайними точками , , множества двойственных дележей. Так как вектор является крайней точкой С-ядра и совпадает с , то все -симплекные игры () удовлетворяют (15). ÿ

Следующий пример показывает, что описанное в утверждении 3 множество сбалансированных игр не совпадает с объединением двойственно -симплексных игр, .

Пример 3. Вернемся к игре трех лиц из примера 2

, , , , , , .

Игра не двойственно -симплексная для любой коалиции , т.к. крайние точки и С-ядра не являются крайними токами множества двойственных дележей. Вклады игроков в максимальную коалицию равны:

, , .

Игра удовлетворяет условию (15) для :

, , , ,

Полученные в утверждениях 1-3 достаточные условия выделяют подмножества, содержащие некоторые известные классы сбалансированных игр. Для вывода использовались базисы, соответствующие однородным минимальным сбалансированным множествам. Выбирая другие базисы, можно выделить подмножества игр, содержащие обобщенные игры большого босса, а также игры с "элементами выпуклости" (перестановочно-выпуклые, в частности, выпуклые игры и игры с CoMa свойством).

Достаточные условия, полученные с помощью базисов, определяющих (для целочисленной функции ) целочисленные базисные решения , являются также достаточными условиями существования С-ядра дискретной игры [6]. Примерами таких условий являются (8), (14) и (15).

Литература:

1. Shapley L. S. On balanced sets and cores // Naval Research Logistics Quarterly. 1967. V. 14. P. 453-460.

2. Бондарева О.Н. Некоторые применения методов линейного программирования к теории кооперативных игр // Проблемы кибернетики. 1963. Вып. 10. М.: Физматгиз. С. 119-140.

3. Branzei R., Tijs S. Additivity regions for solutions in cooperative game theory // Libertas Mathematica. 2001. V. XXI. P. 155-167.

4. Driessen T.S.H., Tijs S.H. The t -value, the nucleolus and the core for a subclass of games // Methods Operations Research. 1983. V. 46. P. 395–406.

5. Branzei R., Tijs S.H. Cooperative games with a simplical core // Balkan Journal of Geometry and Application. 2001. № 6. P. 7-15.

6. Zinchenko A.B. Set-valued solutions for cooperative game with integer side payments // Applied Mathematical Sciences. 2014. V. 11. № 8. P. 541–548.