Dr. Sci. Tech. Smetankina
N.V., Cand. Tech. Sci. Smetankin V.A.,
Smetankin A.V.
The A.N. Podgorny
Institute for Mechanical Engineering Problems of the National Academy of
Sciences of Ukraine, Ukraine
Optimal
arrangement of hydrodynamic radiators
The ultrasonic technics is
widely applied for clearing of details and fluids [1]. However, specific
conditions of technological process of wool clearing restrict ultrasound
application. Complexity of removal of pollution and high requirements to
quality of wool fibers after technological operations leads to that washing is
one most labour-consuming operations [2–4].
The present work deals
with a solution of the problem about an optimal arrangement of hydrodynamic
radiators for a uniform distribution of ultrasonic field parameters and improvement
of wool clearing process.
The radiator consists of a
conic-cylindrical nozzle, a reflector and resonant oscillatory system in the
form of the rods located along the forming cylinder. The converter cylinder has
16 rods in width of 6 mm through 22.5 degrees. The ends of rods are rigidly fixed.
The length of the cylinder is equal 126 mm, and its diameter of 37 mm. The
stream from a nozzle energizes the bending vibration in the rod. The outflow velocity
of fluid is 
km/s, the
pressure is 0.61 MPa. Radiators are established in the cylindrical tank
filled with a liquid with surface-active substances. Its density is equal 1010
kg/m3, the sound velocity is 
km/s, the kinematical viscosity 
m2/s. The intensity
of one radiator is 
Âò/ñì2.
For effective operation of
a radiator it is necessary to select such geometrical and mechanical parameters
that its frequency was close to frequency of the first tone of the radiator rod.
Let's construct
mathematical model of studied process. The equation of transverse vibrations of
the rod under the impulse force 
suddenly affixed in point 
is of the form
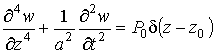, (1)
where 
is Dirac
delta-function in
the point 
;
,
is Young's modulus for
the material of the rod, 
is density for the material
of the rod, 
and 
is width and height of
cross-section of the rod.
The solution of the
equation (1) has the form
,
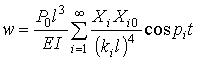where 
is length of the radiator
rod; 
are fundamental circular
frequencies of vibrations; 
are normal functions of the
problem,
;
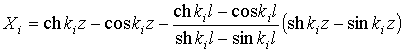is value of normal function
in the point 
. It was accepted that 
.
Fundamental frequencies of radiator
vibrations 
are defined as
.
The frequency of the first
tone calculated according to this formula is equal 1750 Hz. In technical calculations fundamental
frequency of radiator rods is defined by the formula [4]
,
where 
. It is 1767 Hz. Thus, for effective operation of radiators it
is necessary to select such parameters that radiator frequency was close to
frequency of the first tone.
The general equations of fluid
and gas dynamics follows from three main principles: conservation relations of
masses; the law on equality between an impulse of forces and a corresponding
increment of quantity of movement; the law of energy conservation.
Theoretical and
experimental researches show [4] that radiators at their immersing in a fluid on
depth of 0.2–0.3 m can be observed as spherical sources of the zero order, and
the estimation of efficiency of their operation in the closed areas can be made
on magnitude of a sound pressure. In this case expressions for sound pressure 
and velocity of movement of
environment 
, 
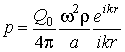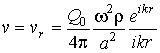, (2)
where 
is the productivity of a sound source,
is the sound velocity; 
, 
is the circular
frequency of vibrations;
,
are cylindrical coordinates.
Intensity of the sound
field of a dot source is calculated by the formula
.
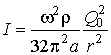Characteristics of the
sound field were defined from Euler's nonlinear equations in the form of Navier-Stokes
jointly with the equation of a condition
, (3)
, (4)
, (5)
where 
is density of the liquid
environment.
The solution of system of
the nonlinear differential equations was carried out by an iteration method.
As the first iteration it
was supposed, that the radiator is replaced with equivalent system of the dot
sources (2). The solution of the homogeneous equations (3), (4) is the generalized
potential of a simple layer. On the found velocity from the equations (4) the
density and pressure of a fluid is defined. The following stage consists in
calculation of the right part of the equations (3), construction of the common solution
of system (3)–(5) and refinement of values of density and pressure of a fluid. Process
is completed at reaching of demanded exactitude of the solution. The system (3)–(5)
also considers attenuation of vibrations of the sound field connected with
viscosity of environment.
The cylindrical tank construction
allows moving circular systems of hydrodynamic radiators along altitude within
0.15 m. We investigate parameters of the ultrasonic field in the radial
cross-sections along tank altitude at various levels of arrangement of hydrodynamic
radiators and solve an optimization problem. The problem is stated in terms of
nonlinear programming.
The design variables are levels
of arrangement of hydrodynamic radiators 
and 
, and along altitude the first radiator occupies a segment 
, the second one 
, where 
m is the length of a radiator.
This domain is defined by the system of following inequalities 
, 
. The objective function is sound pressure, and consequently,
and an oscillating velocity.
The optimization problem
was solved by the effective hybrid optimization method with adaptive control of
the extremum search process [5]. Obviously, the selection of any one method
that would allow as a whole to efficiently solve the stated optimization
problem is highly problematic because at different steps the conditions of
extremum search are different. The method used is based on the concept of
hybridization. It supposes that for a given set of search methods - hybrid elements,
a method is organized which in case of a change of the situation definitively
automatically introduces one or several hybrid elements from the accepted set
due to adaptive control. Hence, the hybrid method can effectively solve a more
wide class of problems than each one of the hybrid elements.
In the given modification
of the method, the hybrid elements are selected so that they implement both the
ravine method of extremum search and movement along the boundary of the
admissible domain. Taken into account thereat are both linear and nonlinear
constraints as well as the possibility of finding the point of extremum within
the admissible domain.
First
the optimization problem for a sound pressure and an oscillating velocity in points from the admissible domain has been
solved.
We finally obtain that in
points 
, 
, 
m and 
m, 
, 
m the maximum values
of the objective function are attained at 
m.
Let's consider the point 
, 
, 
m which removed from the
system of hydrodynamic radiators. In this case the field is arranged uniformly.
Some raise of sound pressure is observed at 
m.
The analysis of the
solution has showed, that there are two values of each of design variables at
which optimum distribution of the objective function on the tank altitude is
possible. We consider the sound pressure in the radial cross-section 
, 
m. Pressure distribution
is symmetrical concerning an axis 
. Two extremums of the objective function are found in points
m, 
m and 
m, 
m.
The coordinate 
corresponds to arrangement of
the first circle of hydrodynamic radiators, and the coordinate 
corresponds to the cross-section
in the middle of radiators. A sound pressure in the abovementioned points has a
maximum value 1846.9 Pa. At removal from extremums the values of pressure
decrease, that corresponds to earlier obtained results [6]. The oscillating
velocity has an analogous distribution.
Consider the case when 
m, 
m. A sound pressure also has two
extremums 1776.8 Pa in points 
m, 
m and 
m, 
m. Character of pressure
distribution in an area moved from system of hydrodynamic radiators practically
does not vary, but values of pressure were a little augmented in the area which
is adjoining to upper edge of a tank. The analogous distribution is observed
for an oscillating velocity.
Thus, at
transition of circular systems of hydrodynamic radiators within 0.15 m the
qualitative character of the ultrasonic field on tank altitude does not change;
however, the maximum values of field characteristics inappreciably decrease.
In an area moved from
hydrodynamic radiators, the maximum values of field characteristics increase.
Hence, for the uniform distribution of parameters of the ultrasonic field along
the tank altitude it is necessary to change altitude of arrangement of
hydrodynamic radiators.
References:
1. Suharkov O.V. Research of Process
Emulsification in a Multifrequency Acoustic Field // Acoustic Bulletin. – 2009.
– Vol. 12, N 4. – P. 57–64.
2. Scherbak Ya.V. Application
of Hydrodynamic Radiators for an Intensification of Processes of Washing of Fibrous
Materials // Bulletin of National Technical University "KhPI". – 2011.–
N 4. – P. 137–140.
3. Physical Fundamentals of Ultrasonic
Technology / edited by L.D. Rosenberg. – Moscow: Nauka, 1970.– 688 p.
4. Ultrasound. Small Encyclopedia.
– Moscow: Soviet Encyclopedia, 1979. – 400 p.
5. Smetankina N.V.
Nonstationary Deformation, Thermoelasticity and Optimization of Multilayer Plates
and Cylindrical Shells. – Kharkov: Miskdruk, 2011.– 376 p.
6. Smetankin V.A., Smetankina
N.V., Smetankin A.V. Theoretical Research of Operation of Hydrodynamic Radiators
in Closed Areas // Materialy VIII Mezinarodni vedecko-prakticka konference “Dny
vedy-2012”.– Dil 82. Matematika.– Praha: Publishing House “Education and
Science”, 2012.– S. 44–46.