К.ф.-м.н. Нечипоренко Н.А., к.ф-м.н. Белая Н.И.

Запорожский национальный технический университет, Украина

Об одной задаче восстановления монотонных функций

Пусть V_{a, A} - класс табличных функций g={g₁, g₂, … , g_N}, удовлетворяющим следующим условиям:

1) (1)

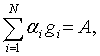2) (2)

где и A - заданные вещественные числа.

Требуется восстановить функцию j = {j₁, j₂, … , j_N}, принадлежащую классу V_{a, A} и заданную своими приближенными значениями f = {f₁, f₂, … ,f_N}. В качестве восстанавливающей примем функцию y Î V_{a, A} , которая удовлетворяет условию

(3)

где d(g) - мера приближения функции f функцией g:

Решим сначала следующую вспомогательную задачу.

Пусть требуется найти функцию y є V, такую, что

(4)

где V – множество табличных функций g, удовлетворяющим условиям (1).

Рассмотрим следующий пошаговый алгоритм A.

Шаг 1. Положить s = 2, k₁ = 0,

Шаг 2. Вычислить

Шаг 3. Найти , где .

Шаг 4. Проверить: ? Если да, то положить

в противном случае положить .

Шаг 5. Проверить < N ? Если да, то перейти к шагу 6, в противном случае закончить вычисления.

Шаг 6. Положить , и перейти к шагу 2.

Нетрудно доказать, что справедлива

Теорема 1. Алгоритм A дает решение задачи (4).

Перейдем теперь к решению задачи (3).

Пусть функция y построена в результате выполнения алгоритма A и является, следовательно, решением задачи (4). Если оказалось, что 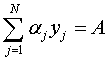, то решение задачи (3) найдено.

Пусть это не так и 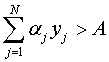. Так как , то для выполнения условия (2) необходимо уменьшить значения функции y. Попытаемся удовлетворить условиям (1) и (2), уменьшая значения y_j так, чтобы оставалось справедливым соотношение

. (5)

Обозначим I={1,2,…,N}. 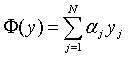, и сохраняя обозначения, принятые в алгоритме А, рассмотрим следующий алгоритм В.

Шаг 1. Положить i=1,

Шаг 2. Положить r_i = m_i+1 .

Шаг 3. Определить J={k_i +1, …,r_i -1}.

Шаг 4. Найти

Шаг 5. Положить где

Шаг 6. Проверить: Ф(y) = A ? Если да, то закончить вычисления.

Шаг 7. Проверить Ф(y) >A ? Если да, то перейти к шагу 9.

Шаг 8. Положить где и закончить вычисления.

Шаг 9. Проверить ? Если да, то перейти к шагу 11.

Шаг 10. Проверить l_i > k_i + 1 ? Если да, то положить r_i = l_i и перейти к шагу 3.

Шаг 11. Проверить i=s-1? Если да, то закончить вычисления.

Шаг 12. Положить i=i+1, и перейти к шагу 2.

Теорема 2. Пусть y – функция, полученная в результате последовательного выполнения алгоритмов А и В. Тогда y является либо решением задачи (3), либо минимизирует функционал Ф(y) на множестве табличных функций, удовлетворяющих соотношениям (1), (5).

Доказательство. Докажем сначала первую часть утверждения.

Построенная функция y удовлетворяет условиям (1), (5) – это обеспечивается на шаге 5 алгоритма В. Пусть y удовлетворяет также условию (2). Тогда, учитывая, что , приходим к выводу, что y – решение задачи (3).

Предположим теперь, что для некоторого i, , после выполнения шага 5 алгоритма А оказалось Ф(y) < A, то есть Но поскольку , то будет существовать такое, что увеличив значения на величину ε₁, получим функцию, удовлетворяющую соотношениям (1), (5) и (2), то есть являющуюся решением задачи (3). Очевидно, что ε₁ можно определить из уравнения

Рассмотрим теперь случай, когда в результате выполнения алгоритмов А и В построена функция y такая, что Ф(y) > А. Покажем, что y доставляет функционалу Ф(у) минимальное значение на указанном в теореме множестве функций.

Предположим противное. Пусть существует табличная функция g, удовлетворяющая соотношениям (1), (5), и такая, что Ф(g) < Ф(y).

Поскольку все , то будет существовать n, такое, что

g_n < y_n (6)

Так как по предположению функция g удовлетворяет условию (5), то индекс n не должен совпадать с теми индексами j, для которых

Но тогда для некоторого j, j<n, будет справедливо соотношение g_j>g_n, что противоречит условию монотонности функции g.

Теорема доказана.

Предположим, что в результате выполнения алгоритмов А и В решение задачи (3) не найдено. Это означает, что мы не можем добиться выполнения соотношения (2), если значения удовлетворяют условиям (1), (5). Попытаемся удовлетворить этому соотношению, уменьшая значения так, чтобы оставались справедливыми соотношения (1) и

(7)

где

Обозначим M={1,2,…,s-1} и, сохраняя принятые ранее обозначения, рассмотрим следующий алгоритм С.

Шаг 1. Найти

Шаг 2. Определить J={r}, K={k_r+1, …, k_r+1}.

Шаг 3. Положить M=M \ J.

Шаг 4. Проверить Ø ? Если да, то перейти к шагу (15).

Шаг 5. Найти

Шаг 6. Вычислить Δ = min(Δ₁, Δ₂), где

Шаг 7. Положить .

Шаг 8. Проверить Ф(y) = A ? Если да, то закончить вычисления.

Шаг 9. Проверить Ф(y) > A ? Если да, то перейти к шагу 11.

Шаг 10. Положить где

и закончить вычисления.

Шаг 11. Проверить : Δ < Δ₁ ? Если да, то перейти к шагу 14.

Шаг 12. Положить

.

Шаг 13. Проверить ? Если да, то перейти к шагу 6.

Шаг 14. Положить и перейти к шагу 3.

Шаг 15. Положить i=2.

Шаг 16. Проверить ? Если да, то перейти к шагу 18.

Шаг 17. Проверить i < s-1 ? Если да, то перейти к шагу 21, иначе закончить вычисления.

Шаг 18. Вычислить

Шаг 19. Положить

Шаг 20. Выполнить шаги 3-11 алгоритма В, предварительно заменив на шаге 5 величину δ_i на δ.

Шаг 21. Положить i=i+1 и перейти к шагу 16.

Аналогично теореме 2 может быть доказана

Теорема 3. Пусть y – функция, полученная в результате последовательного выполнения алгоритмов А, В и С. Тогда y либо является решением задачи (3), либо минимизирует функционал Ф(y) на множестве табличных функций, удовлетворяющих соотношениям (1), (7).

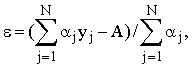
Теорема 4. Пусть функция y={y₁, y₂, …, y_N } построена в результате последовательного выполнения алгоритмов А, В, С и Ф(y) > A. Тогда функция где

является решением задачи (3).

Доказательство. Функция удовлетворяет условиям (1) и (2). Действительно, монотонность y^* из монотонности y, а справедливость (2) обуславливается выбором ε как корня уравнения .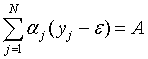

Поэтому осталось показать, что

Предположим противное. Пусть существует функция такая, что Поскольку согласно алгоритму С

то и где

Тогда и, следовательно,

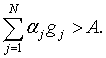
Таким образом, предположение вступает в противоречие с условием (2) для функции g.

Теорема доказана.

Аналогично рассматривается случай, когда Ф(y) < A. Решение задачи, как и ранее, осуществляется следующим образом: последовательно максимизируется Ф(y) на следующих классах табличных функций:

1) удовлетворяющих условиям (1), (5) (алгоритм В₁);

2) удовлетворяющих условиям (1), (7) (алгоритм С₁).

Алгоритмы решения этих задач аналогичны алгоритмам В и С соответственно.

Как и выше, можно показать, что последовательное применение алгоритмов А, В₁, С₁ позволяет построить функцию y, которая либо является решением задачи (3), либо максимизирует функционал Ф(y) на множестве табличных функций, удовлетворяющих условиям (1), (7), и тогда решением задачи (3) является функция y^*={y₁+e, y₂+e, … y_N+e},

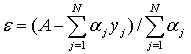
где

В заключении заметим, что используя полученные значения сеточной функции, обладающей свойствами (1) - (3), можно построить функцию с требуемыми свойствами гладкости [1], [2].

Литература:

1. Нечипоренко Н. А. (1993) Об оптимальном по точности восстановлении монотонных функций. Кибернетика и вычислительная техника. – Вып. 97. 106-111.

2. Смоляк С.А. (2010). Восстановление гладких монотонных функций. – Прикладная эконометрика, 2(18). 123-139.