Математика/5. Математическое моделирование

 

Аманбаев Т.Р., Тилеуов Г.Е., Мамешов Б., Курманалиева А.

Южно-Казахстанский государственный университет им. М. Ауэзова, Институт математики и математического моделирования КН МОН, Казахстан

 

Течение ультрадисперсной смеси в канале с внезапным расширением при наличии процессов коагуляции и конденсации

 

Многофазные дисперсные системы часто встречаются в различных областях современной техники. Особое значение имеет изучение движений дисперсных сред в различных каналах, в частности, переменного сечения. Исследование течений дисперсных сред является одной из актуальных проблем динамики и теплофизики многофазных систем [1]. В последние годы процессы фазовых превращений в различных средах стали использовать для получения наноразмерных (ультрадисперсных) частиц в расширяющихся каналах за счет зародышеобразования (нуклеации) и их роста [2,3]. При этом для описания процесса роста зародышей используются различные модели, в частности, монодисперсная модель, в которой предполагается наличие коагуляции зародышей. Коагуляция (слияние) частиц является одной из основных причин эволюции дисперсных систем. Это явление наблюдается в различных физических ситуациях и оказывает воздействие на рост кластеров в растворах и газодисперсных системах.

Рассмотрим течение двухфазной дисперсной смеси в канале с внезапным расширением. Для моделирования движения таких сред используем уравнения и замыкающие соотношения механики многофазных сред [1], которые ввиду малости размеров зародышей жидкой фазы запишем в квазиравновесном приближении, когда скорости и температуры фаз совпадают, а на межфазной поверхности происходят фазовые превращения, при этом в системе имеет место коагуляция дисперсных включений

, ,   ,             (1)      

,    ,                                     (2)

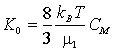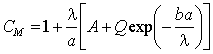,  ,   ,   ,  ,   ,  ,   ,   ,    ,          (3),     ,     .       (4)

Здесь αi , , ρi , ci – объемные доли, истинные и приведенные плотности, а также теплоемкости несущей (i=1) и дисперсной (i=2) фаз; ρ, p, T, e, E,  - плотность, давление, температура, внутренняя и полная энергии, вектор скорости эффективной среды (равновесной смеси газовой и дисперсной фаз);

, ,  - интенсивность фазового перехода (конденсации), коэффициент коагуляции зародышей, обусловленной их броуновским движением и постоянная Больцмана; n, a – концентрация и радиус микрокапель. Температура насыщения  удовлетворяет уравнению Клапейрона-Клаузиуса.

Процесс кластеризации в высокоскоростных потоках можно разделить на две стадии [2]. На первой стадии определяющим является процесс образования зародышей критического размера, на второй – процессы конденсационного роста и коагуляции вновь образовавшихся зародышей, когда нуклеацию можно не учитывать. Хотя в ряде случаев одновременно протекают оба процесса, такое разделение представляется вполне разумным.

Учитывая вышесказанное, будем полагать, что на первой стадии из-за процесса нуклеации в узком канале непрерывно появляются зародыши жидкой фазы. Затем при течении сформированной газодисперсной смеси в расширенной части канала осуществляются процессы коагуляции и конденсационного роста зародышей. С учетом симметрии течения для постановки задачи зададим следующие граничные условия на входе в расширяющуюся часть канала (h – ширина узкой части канала): x=0, 0≤y≤h/2: , , ,  ,  ,  u=u0,  v=0,  . Вдоль оси х примем условие симметрии, на твердых границах – условие непротекания, а на свободной границе – условие непрерывности течения. В качестве начальных условий в расширенной части канала примем условия невозмущенной газовой фазы (без зародышей жидкой фазы).

Для определения критического размера зародышей  и их концентрации  используем молекулярно-кинетическую теорию процесса гомогенной нуклеации (зародышеобразования), которая была заложена в работах ряда исследователей [1].

Поставленную задачу решим численным методом крупных частиц [4]. Расчеты проведены для пара воды. Начальные значения определяющих параметров на входе в канал следующие: давление =1МПа, температура насыщения =453К, число Маха на входе , степень переохлаждения пара =0.044. Критический радиус зародышей =0.6 нм. Полуширина узкого канала разделена на 10 ячеек, а расчетная область разбивалась на сетку с размерами 102 ячейки в продольном и 52 ячейки – в поперечном направлениях.

Ниже представлены некоторые результаты расчетов, полученные численным методом крупных частиц. Рис. 1 иллюстрирует распределение приведенной плотности дисперсной фазы (по осям отложены номера ячеек), а рис. 2 - поле скорости смеси на момент времени 0.4 сек после входа в расширяющуюся часть канала (ввиду симметричности течения результаты расчетов показаны лишь для верхней половины расчетной области). Видно, что течение имеет вихревую структуру, причем распределение плотности дисперсной фазы имеет «рогообразный» вид. Следует отметить, что плотность смеси не обладает такой структурой, так что подобное необычное поведение плотности дисперсной фазы не связано с эффектом обтекания обратного уступа (когда за уступом образуется вихревое течение), а обусловлена, по-видимому, наличием процессов массопереноса (коагуляции капелек и конденсации пара на их поверхностях). Результаты показали, что наиболее крупные капли формируются именно в зоне вихря, причем первоначальный радиус капель за счет процессов коагуляции и конденсации увеличивается на расчетный момент времени более чем в 10 раз.

00

 

 

0
 
 

 


Р

 

 

И

 

Рис.1251680768251683840251684864251685888251686912251687936251688960251689984251691008251692032

                                                 Рис. 2

   

Работа выполнена при поддержке гранта (1117/ГФ2) Министерства образования и науки Республики Казахстан.

 

ЛИТЕРАТУРА

 

1.   Нигматулин Р.И. Динамика многофазных сред. В 2-х частях /  Р.И.Нигматулин - М.: Наука, 1987.

2.   Аникеев В.И. Моделирование и расчет процесса быстрого расширения сверхкритического флюида с образованием наночастиц / В.И. Аникеев, Д.А. Степанов, А. Ермакова // Теоретич. основы хим. технол.–2011.–Т.45, №2.–С.155-169.

3.   Jun Li. Two-phase homogenous model for particle formation gas saturated solution process / Li Jun, H.A. Matos, E. Gomes de Azevedo // J. Supercrit. Fluids. – 2004. - V. 32. – P. 275-293.

4.   Белоцерковский О.М. Метод крупных частиц в газовой динамике / О.М. Белоцерковский, Ю.М. Давыдов. – М.: Наука, 1982. – 392 с.