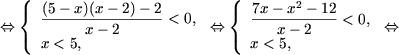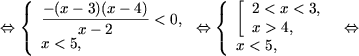Аширбекова Ф.Д.

КГУ « Ош №75 им. Ш. Кудайбердыулы», Алматы

ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА И СПОСОБЫ ИХ РЕШЕНИЯ

В основе теории неравенств лежат утверждения, что все действительные числа разбиваются на положительные, отрицательные числа и число ноль. Для того чтобы указать, что число a положительно, пользуются записью a>0. При этом сумма и произведение положительных чисел также являются положительными числами. Это дает возможность ввести в множестве действительных чисел неравенства: по определению a>b, если a – b положительно. Далее, если число a отрицательно, то число – a положительно (и наоборот). Наконец, для любого положительного числа a найдется такое положительное рациональное число r, что r < a.

Основная идея решения неравенства состоит в замене данного неравенства другим, более простым, но равносильным данному; полученное неравенство заменяем более простым равносильным ему неравенством и т. д. Решить неравенство с переменной – значит найти все его решения. Всякое значение переменной, при котором данное неравенство с переменной обращается в верное числовое неравенство, называется решением неравенства. Два неравенства с одной переменной х называются равносильными, если решения этих неравенств совпадают.

Неравенство, содержащее неизвестное под знаком логарифма или в его основании называется логарифмическим неравенством.

Прежде чем говорить о логарифмических неравенствах, необходимо вспомнить определение логарифма и некоторые его свойства.

Логарифмом числа b по основанию a называется степень, в которую нужно возвести число a, чтобы получить число b и обозначается log_a b.

Например,                         

log₂ 4 = 2, так как 2² = 4,

log₃ 81 = 4, так как 3⁴ = 81.

 Логарифм числа должен удовлетворять следующим условиям:

1)  a > 0;

2) a не равно 1;

3) b > 0.

Функция, которая каждому числу x ставит в соответствие его логарифм по некоторому основанию (например, a), называется логарифмической функцией и обычно обозначается так: y = log_a x.

 При a > 1 логарифмическая функция возрастает, а при 0 < a < 1 логарифмическая функция убывает. Эти свойства очень важны и понадобятся при решении неравенств.

Чтобы решить логарифмическое неравенство, необходимо выполнить следующую цепочку действий:

1) привести неравенство к виду log_a f(x) > log_b g(x) (можно приводить к аналогичному виду со знаками <, ≥, ≤.

Обычно приведение исходного неравенства к такому виду осуществляется с помощью использования различных свойств логарифма.

При приведении неравенства к указанному виду нужно обязательно учитывать область определения исходного неравенства.

2) дальше возможно 2 случая:

a) если a > 1, то составляем систему:

{f(x) > 0

{g(x) > 0

{f(x) > g(x);

Здесь первые два неравенства – это пункт 3)  из определения логарифма. Третье условие вытекает из того, что логарифмическая функция возрастает при a > 1.

В этой системе первое неравенство является избыточным, его можно не писать, так как оно легко получается из второго и третьего.

b) если 0 < a < 1, то составляем систему:

{f(x) > 0

{g(x) > 0

{f(x) < g(x);

Третье условие вытекает из того, что логарифмическая функция убывает при 0 < a < 1. А в этой системе уже второе неравенство является избыточным.

Пример 1. Решить неравенство log₂ (x – 2) + log₂ (x – 3) ≤1.

Решение.

1) Воспользуемся свойством логарифма: log₂ (x – 2)(x – 3) ≤ 1.

Теперь представим 1 как log₂ 2: log₂ (x – 2)(x – 3) ≤ log₂ 2.

2) Составляем систему:

{(x – 2)(x – 3) > 0

{(x – 2)(x – 3) ≤2,

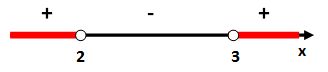
Решим отдельно первое неравенство методом интервалов и получим следующее решение:

[x ≥ 3

[x ≤ 2.

Решим отдельно второе неравенство.

(x – 2)(x – 3) ≤ 2,

x² – 5x + 6 ≤ 2,

x² – 5x + 4 ≤ 0,

D = 25 – 16 = 9,

x1 = (5 + 3)/2 = 4,

x2 = (5 – 3)/2 = 1.

(x – 4)(x – 1) ≤ 0.

Получим следующее решение:

1 ≤ x ≤ 4.

А тогда решение исходной системы: x € [1; 2] U [3; 4].

Однако нужно еще учесть область определения исходного неравенства:

x – 2 > 0

x – 3 > 0,

то есть x > 3.

А тогда, учитывая область определения исходного неравенства, получим: x € (3; 4].

Ответ: x € (3; 4].

Пример 2. Решить неравенство log_1/2 (16 + 4x – x²) ≤ -4.

Решение.

1)Известно, что -4 = log_1/2 16.

Тогда получаем неравенство log_1/2 (16 + 4x – x²) ≤ log_1/2 16.

2) Составляем систему:

{16 + 4x – x² > 0,

{16 + 4x – x² ≥ 16.

Третьего неравенства здесь не будет, так как очевидно, что 16 > 0.

Заметим, что первое неравенство системы решать необязательно, ведь если 16 + 4x – x² ≥ 16, то понятно, что оно будет больше 0. Поэтому остается решить только второе неравенство системы.

Решаем его:

-x² + 4x + 16 ≥ 16,

-x² + 4x ≥ 0,

x² – 4x ≤ 0,

x(x – 4) ≤ 0.

Применим метод интервалов и получим ответ: x € [0; 4].

Ответ: x € [0; 4]

В процессе решения логарифмических неравенств часто используются следующие утверждения относительно равносильности неравенств и учитываются свойства монотонности логарифмической функции.

Утверждение 1. Если a > 1, то неравенство log_a f(x) > log_a g(x) равносильно системе неравенств

	f(x) > g(x),
	g(x) > 0.

Утверждение 2. Если 0 < a < 1, то неравенство log_a f(x) > log_a g(x) равносильно системе неравенств

	f(x) < g(x),
	f(x) > 0.

Утверждение 3. Неравенство log_h(x) f(x) > log_h(x) g(x) равносильно совокупности систем неравенств

		h(x) > 1,
		f(x) > g(x) > 0,
		0 < h(x) < 1,
		0 < f(x) < g(x).

Подчеркнем, что в неравенстве log_a f(x) > log_a g(x) вместо знака > может фигурировать любой из знаков ≥ , < , ≤ . В этом случае утверждения 1-3 соответственно преобразуются.

Пример3. Решить неравенства

a) log3(x^2 - x) ≥ log3(x + 8);	d)
b)	e) log2x(x^2 - 5x + 6) < 1.
c)

Решение. a) Используя утверждение 1 , получим

log3(x^2 - x) ≥ log3(x + 8) Û	x^2 - x ≥ x + 8,	Û	x^2 - 2x - 8 ≥ 0,	Û
	x+8 > 0,		x > -8,

Û		x ≤ -2,
		x ≥ 4,	Û x Î (-8;-2]È[4;+¥).
		x > -8,

b) Основание логарифма - число между нулем и единицей, поэтому, используя утверждение 2, получим

c) Запишем 0 = log₂1 и, используя утверждение 1, получим

Запишем и, используя утверждение 2, получим

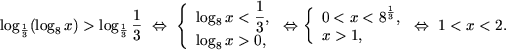
Таким образом, любое логарифмическое неравенство сводится в конечном счете к неравенству вида log_a f(x) > log_a g(x), где, как обычно, a>0 и a 1.

Литература

1. Куланин Е.Д. 3000 конкурсных задач по математике. М.: Айрис Ролиф, 1997

2. Мордкович А.Г. Алгебра и начала анализа. М.: Высшая школа, 1997