технические
науки/ 2.механика
аспирант
Прокопенко В.С., магистр 1-го курса Орехова Т.Н.
студент 3-го
курса Решетов А.В.
Белгородский государственный технологический
университет им. В.Г. Шухова
Анализ методики
расчета к.п.д. сепаратора
Для проведения анализа
методики расчета к.п.д. сепаратора воспользуемся формулами предложенными
Розином – Раммлером и Хейдом [1,2,3].
Для частиц любого
размера δ, содержащихся в исходном материале из соображений материального
баланса справедливо выражение:
![]() ,
,
или (1)
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() - массовое количество
частиц с размером
- массовое количество
частиц с размером ![]() .
.
Таким образом,
фактический относительный выход тонкого продукта разделения равен:
![]() ,
(2)
,
(2)
где
![]() - кратность
циркуляции пыли в системе мельница – сепаратор.
- кратность
циркуляции пыли в системе мельница – сепаратор.
Максимально возможный
выход тонкого продукта, содержащего только частицы размером ![]() , имел бы место при
, имел бы место при ![]() и согласно (2) был бы
равен:
и согласно (2) был бы
равен:
![]() , (3)
, (3)
Таким образом, к.п.д.
сепаратора по тонкому продукту, рассчитанный по размеру частиц δ равен:
![]() , (4)
, (4)
Аналогично может быть
получен к.п.д. сепаратора по грубому продукту для частиц размера δ:
![]() , (5)
, (5)
Из уравнений (4), (5)
следуют выражения для расчета выходов продуктов разделения
![]() ,
(6)
,
(6)
![]() ,
(7)
,
(7)
Из уравнения (2)
следует:
![]() ; (8)
; (8)
Введем обозначения для
каждого размера частиц:
![]() - экспериментальные
значения остатков;
- экспериментальные
значения остатков;
![]() - поправки к
экспериментальным значениям остатков;
- поправки к
экспериментальным значениям остатков;
![]() - невязка баланса;
- невязка баланса;
![]() , (9)
, (9)
Тогда с учетом
поправок выражение (8) примет вид:
![]() , (10)
, (10)
откуда
![]() , (11)
, (11)
![]() . (12)
. (12)
Обозначив ![]() и подставив сюда
значение
и подставив сюда
значение ![]() получим:
получим:
![]() . (13)
. (13)
Найдем значения ![]() и
и ![]() при которых значение z минимально:
при которых значение z минимально:
![]() , (14)
, (14)
![]() . (15)
. (15)
Решая эти уравнения
получаем:
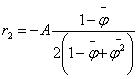 , (16)
, (16)
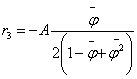 . (17)
. (17)
Подставляя (16) и (17)
в (12) получаем:
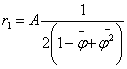 . (18)
. (18)
Формула (4) для
расчета к.п.д. сепаратора учитывает лишь степень выноса из сепаратора в тонкий
продукт частиц с размером
меньше δ и не учитывает попадания в
него крупных (больше δ) частиц. Формула (5), наоборот, учитывает лишь
степень выделения из сепаратора в грубый продукт частиц с размером больше
δ и не учитывает попадание в него мелких (меньше δ) частиц.
Несколько более совершенной является
формула Дина – Уайта [4]:
![]() , (19)
, (19)
где
![]() - условный
безразмерный показатель, учитывающий степень извлечения (выноса) мелких частиц
в готовый продукт и степень проскока в него крупных частиц.
- условный
безразмерный показатель, учитывающий степень извлечения (выноса) мелких частиц
в готовый продукт и степень проскока в него крупных частиц.
Представим величину ![]() следующим образом:
следующим образом:
![]() , (20)
, (20)
где
![]() - к.п.д. сепаратора
по формуле Розина (4)
- к.п.д. сепаратора
по формуле Розина (4)
![]() - доля крупных частиц
попавших в тонкий продукт;
- доля крупных частиц
попавших в тонкий продукт;
![]() . (21)
. (21)
К аналогичным конечным
выражениям пришли и другие авторы [5]. Они рассматривали величину ![]() как отношение массы
какой либо классифицированной узкой фракции в любом из двух продуктов
разделения к массе той же фракции в исходном продукте. Величина
как отношение массы
какой либо классифицированной узкой фракции в любом из двух продуктов
разделения к массе той же фракции в исходном продукте. Величина ![]() определяется двумя
способами:
определяется двумя
способами:
1)
При расчете по грубому
продукту
![]() , (22)
, (22)
2)
При расчете по тонкому продукту
![]() .
(23)
.
(23)
Эти формулы легко
преобразуются в (13)
Несколько
видоизмененная формула предложена В. А. Гудемчуком:
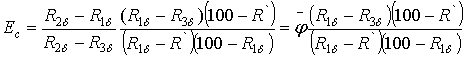 , (24)
, (24)
где
![]() - остаток
кондиционного продукта на заданном сите.
- остаток
кондиционного продукта на заданном сите.
Если формулы (4), (5)
выражают степень извлечения частиц с размером меньшим или большим определенной
величины, а формула (20) характеризует степень «чистоты» получаемых продуктов,
то формула (24) характеризует процесс сепарации как с точки зрения
эффективности извлечения, так и в отношении «чистоты» разделения. При этом
величина к.п.д. не зависит от того, ведется ли оценка сепарации по грубому или
тонкому продукту.
Проведя анализ
методики расчета к.п.д. сепаратора отметим следующие основные недостатки всех
рассмотренных формул.
1.
К.п.д. сепаратора
зависит от выбора размера отверстий сита δ или остатка на этом сите ![]() [в формуле (24) – от
размера сита на котором определяется остаток кондиционного продукта R`]. В
зависимости от выбора
[в формуле (24) – от
размера сита на котором определяется остаток кондиционного продукта R`]. В
зависимости от выбора ![]() к.п.д. одного и того
же сепаратора при одних и тех же условиях и работе на одном и том же исходном
материале может иметь величину, изменяющуюся в самых широких пределах.
к.п.д. одного и того
же сепаратора при одних и тех же условиях и работе на одном и том же исходном
материале может иметь величину, изменяющуюся в самых широких пределах.
2.
Величина к.п.д. даже при
одинаковой выбранной величине δ весьма сильно зависит от состава исходного
продукта [4].
Список литературы.
1.
Ушаков С.Г., Мизонов В.Е. Аэродинамическая классификация порошков М:
Химия, 1989, 160с.
2.
Ушаков С.Г., Зверев Н.И. Инерционная сепарация пыли.- М.."Энергия,
1974, 165 с.
3.
Rumpf H., Leschonski К. Prinzipen und neuere Verfahren der Wind sichtung. - «Chem. Ing. Tech.», 1967, Bd 39, S.21.
4.
Барский М.Д.Фракционирование порошков - M.:
Недра, 1980, 327с.
5.
Separaion - the superdinamic way
« World Gement» , 1985 , 5