Коллинеарные
решения фотогравитационной ограниченной эллиптической задачи трех тел
Турешбаев А.Т., Омарова У.Ш., Мырзахметова
С.Е.
Для небесной механики и динамики
космических полетов наиболее важной является ограниченная фотогравитационная
задача трех тел, в которой изучается движение тела P
малой массы m под
действием ньютоновского притяжения и репульсивной силы светового давления двух основных излучающих тел,
обладающих точечными массами m1 и m2 (m1³m2>>m),
которые обращаются друг относительно друга по кеплеровым орбитам, определяемым
задачей двух тел. При этом сила светового давления, обратно пропорциональная
квадрату расстояние до излучающего тела, зависит не только от интенсивности
источника излучения, но и от парусности частицы, определяемый отношением
“сечение/масса”. Следовательно, динамической моделью, адекватно описывающей движение
частицы (частицы газопылевых облаков в космическом пространстве,
спутников-баллонов, а также кораблей-парусников) в поле двух основных
гравитирующих и одновременно излучающих тел, является фотогравитационная ограниченная задача трех тел.
Выберем прямоугольную систему
координат OXYZ, начало которой
поместим в центр масс тел; ось OX
направим вдоль прямой, соединяющей основные излучающие тела S1 и S2, а ось Z – перпендикулярно плоскости орбитального
движения в сторону, откуда вращение системы тел видно происходящим против хода
часовой стрелки. При этом для удобства выберем следующие единицы измерения:
сумму масс m1 и m2 основных тел примем за единицу массы,
расстояние между ними – за единицу длины, отношение T/2p - за единицу времени (где T – период обращения тел друг относительно
друга). Тогда уравнения частицы P можно записать в виде
![]()
![]() (1)
(1)
![]()
где ![]() - силовая функция,
- силовая функция,
q1Î(-¥; 1]
и q2Î(-¥; 1]
- коэффициенты редукции массы, характеризующее суммарное воздействие
гравитационной и радиационной репульсивной сил на частицу, ![]() и
и ![]() - расстояние
частицы до основных тел, 1-m и m - их безразмерные массы, r = p
/ (1+e cos J) – расстоянии между основными телами (p и e
– параметр и эксцентриситет их кеплеровой орбиты), J - истинная аномалия.
- расстояние
частицы до основных тел, 1-m и m - их безразмерные массы, r = p
/ (1+e cos J) – расстоянии между основными телами (p и e
– параметр и эксцентриситет их кеплеровой орбиты), J - истинная аномалия.
Следуя Нехвилу [Дуб., 1964],
введем в уравнениях (1) замену переменных
X=
r x, Y=
r y, Z=
r z.
После перехода к новой
независимой переменной J, система (1) преобразуется в следующую
систему дифференцированных уравнений:
![]()
![]() (2)
(2)
![]()
Здесь
![]()
![]()
![]()
Система уравнений (2) может иметь
стационарные решения, называемые точками либрации, если выполнены необходимые и
достаточные условия их существования в виде
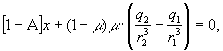
![]() (3)
(3)
![]()
Как видно, последнее уравнение
системы (3) может выполняться лишь при e=0, что указывает на существование
рассматриваемых точек либрации только в круговой задаче. Однако, как видно из
последнего уравнения, при 0<e<<1
вокруг этих точек существуют периодические движения, которые являются
объектом дополнительного исследования.
Рассмотрим коллинеарные точки
либрации, координаты х*
которых определяются при y = z
= 0 из (3) уравнением
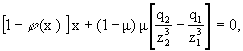 (4)
(4)
где ![]()
Область существования и устойчивости
этих точек (положений относительного равновесия, называемых точками либрации)
определяются как параметрами гравитационно -репульсивного поля, так и
парусностью, находящихся в этом поле частиц. В работе [ ] посредством введения
некоторого обобщенного параметра k,
характеризующего гравитационно - репульсивное поле системы и равного
![]() (5)
(5)
(где Mi- массы основных тел, а Qi – мощности их излучения) была дана весьма геометрически
простая и физически ясная интерпретация картины существования и устойчивости
треугольных точек, либрации. Для фиксированной пары основных тел коэффициенты
редукции, как видно из (5), не могут быть произвольными, что не принималось во
внимание во многих посвященных этой проблеме предыдущих исследованиях.
Введя возмущения, ![]() получим уравнения
возмущенного движения в вариациях
получим уравнения
возмущенного движения в вариациях
![]()
![]() (6)
(6)
![]()
Здесь ![]()
![]() (7)
(7)
Выбранная за независимую переменную, r1 и r2 – расстояния частицы P(x,y,z) до
основных тел, q1 и q2 – коэффициенты
редукции массы частицы, зависящие от интенсивностей излучения и парусности
частицы.
Для случая круговой задачи (e=0) из (3) находим координаты коллинеарных
точек из решения уравнения [ ]
![]() (8 )
(8 )
Корни характеристического
уравнения системы (6) равны
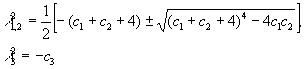 (9)
(9)
Здесь 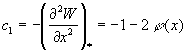
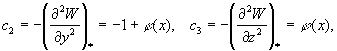
![]()
При выполнении системы неравенств
![]()
![]() (10)
(10)
корни уравнения (9 ) будут чисто мнимыми.
В системе неравенств (10) исключив q1 и q2 с помощью (5) и (8), получим
необходимые условия устойчивости по Ляпунову
в виде
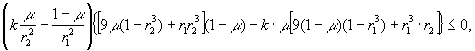 (11)
(11)
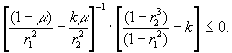
Система неравенств (11) позволяет
установить, что для всякой фиксированной пары основных тел в плоскости (x,k)
существуют целые семейства устойчивых коллинеарных точек либрации, которые
могут быть заполнены бесчисленным множеством частиц различной парусности,
образующих устойчивое скопление газопылевых облаков.