канд. техн. наук В.В. Шутюк, О.В. Бендерська,

канд. техн. наук О.С. Бессараб

Національний університет харчових технологій

Дослідження кінетики осмотичного зневоднення гарбуза

Важливу роль у харчуванні людини відіграють овочі. Їхня корисність зумовлена хімічним складом, енергетичною і біологічною цінністю, фізіологічною та лікувально-профілактичною дією. Серед овочевих культур, які вирощують в Україні, гарбуз займає чільне місце. Цей овоч належить до баштанних культур і нараховує велику кількість видів, з яких у нашій країні вирощують переважно три: крупноплідний (Cucurbita maxima Duch), твердокорковий, або Звичайний столовий (Cucurbita pepo L.), та Мускатний (Cucurbita moschata Ducli) [1].

Останніми роками об’єктом постійної уваги дослідників є осмотичне оброблення фруктів і овочів — зручного способу зниження витрат на процес зневоднення [2]. Цей процес дає можливість зберегти харчові та смакові характеристики продукції, яку піддають подальшому сушінню класичними способами [3] або використовують для отримання проміжних продуктів з поліпшеною стабільністю при зберіганні за допомогою комбінованих методів оброблення [4].

Мета цієї роботи полягала в тому, щоб отримати експериментальні дані кінетики осмотичного зневоднення гарбуза водними розчинами NaCl і сахарози. Використання математичного моделювання процесу дало змогу визначити ефективні коефіцієнти дифузії сахарози і NaCl для розрахунку масоперенесення, пов’язаного з процесом дегідратації.

Для дослідів використовували тверді частини гарбуза Звичайного столового з початковим вологовмістом 91…93 % та вмістом сахарози 3…4 %. Проби отримували із паренхіматозних тканин у вигляді циліндра (діаметр 15 мм, довжина 20 мм).

Аналіз отриманих лабораторних даних показав, що перенесення маси в ході осмотичного зневоднення успішно моделюється за допомогою другого закону дифузії Фіка [5]. При цьому зовнішній опір масообміну незначний порівняно з внутрішнім. Для узагальнення отриманих результатів застосовували еквівалентний радіус циліндрів через мале співвідношення довжини до діаметра зразків (0,75). Еквівалентний радіус використовуваних циліндрів розраховували за рівнянням (1), в якому кожен циліндр замінюється сферою з таким самим об’ємом:

(1)

де V — об’єм зразка, м³.

З урахуванням попередніх припущень та з огляду на нестаціонарний процес осмотичного зневоднення швидкість дифузії можна визначити за допомогою аналітичної залежності стосовно закону Фіка для сфер. Тоді загальні витрати дифундуючої речовини (вода, сахароза або NaCl), що перетинає поверхню сфери в період часу τ, визначають з рівняння [6]

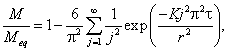(2)

де τ — час, с; eq — рівноважний стан; j — концентрація дифундуючої речовини; K — коефіцієнт дифузії, м²/с.

Рівноважні значення для системи кількості води, концентрації сахарози і хлориду натрію при осмотичному зневодненні гарбуза отримали за рівнянням E. Azuara та ін. [7]:

(3)

де β — емпіричний коефіцієнт; x — характерна величина процесу; k — константа, с^–1; i — технологічні умови процесу (температура, тиск).

Результати опрацьовували з використанням програмного забезпечення Statistica 6.0. Для оптимізації рівноважних значень використовували нелінійний метод найменших квадратів за допомогою інструмента Solve Microsoft1 Excel 97 програмного забезпечення (Microsoft Corporation). Отримані результати дали змогу за рівнянням (3) одержати прогнозні значення концентрації сахарози і хлориду натрію при осмотичному зневодненні гарбуза.

Висновки

Аналіз отриманих лабораторних результатів осмотичного зневоднення гарбуза показує, що при раціональних концентраціях розчину NaCl і сахарози вологовміст сировини може зменшуватись до 47 % від початкового значення.

Розроблена математична модель дає можливість прогнозувати процеси масоперенесення при осмотичному зневодненні, а отже, може бути використана як корисний інструмент під час розроблення та контролю в промисловості.

Література

1. Справочник по овощеводству / В.И. Алексашин, А.В. Алпатьев, Р.А. Андреева и др.; Сост: В.А. Брызгалов. — 2-е изд., перераб. и доп.— Л.: Колос. Ленингр. отд-ние, 1982. — 511 с.

2. Jayaraman, K.S.; Das Gupta, D.K. Dehydration of fruits and vegetables: Recent developments in principles and techniques. Drying Technology 1992, 10 (1), 1–50.

3. Raoult-Wack, A.L. Recent advances in the osmotic dehydration of foods. Trends in Food Science and Technology 1994, 5 (8), 255–260.

4. Riva, M.; Campolongo, S.; Leva, A.A.; Maestrelli, A.; Torreggiani, D. Structure-property relationships in osmo-air-dehydrated apricot cubes. Food Research International 2005, 38 (5), 533–542.

5. Li, H.; Ramaswamy, H.S. Osmotic dehydration of apple cylinders: I. Conventional batch processing conditions. Drying Technology 2006, 24, 619–630.

6. Crank, J. The Mathematics of Diffusion, 2nd Ed.; Oxford University Press: New York, 1975.

7. Azuara, E.; Corteґs, R.; Garcia, H.S.; Beristain, C.I. Kinetic model for osmotic dehydration and its relationship with Fick’s second law. International Journal of Food Science and Technology 1992, 27, 409–418.