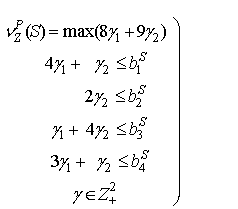Экономические науки/8. Математические методы в экономике

К.ф.-м.н. Зинченко А.Б., Ткачева В.В.

Южный федеральный университет. Россия

Кооперативные производственные игры

Кооперативная игра , где - множество участников, - характеристическая функция, называется LP-игрой (linear programming game), если функция определена задачами линейного программирования

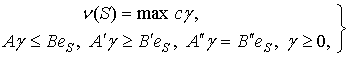(1)

для всех , . При некоторых условиях, соответствующих реальным ситуациям, такие задачи разрешимы, а соответствующие игры – полностью сбалансированы. Известно [1], что каждая полностью сбалансированная игра является минимальной игрой конечного набора аддитивных игр. LP-игры относятся к классу параметрических кооперативных игр, их характеристические функции заданы неявно. Наиболее известными являются следующие подклассы LP-игр.

· Производственные игры (linear production games) [2].

· Депозитные игры (deposit games) [3].

· Игры на сетях (network games) [4], [5].

Данная статья посвящена производственным играм с неделимой продукцией. Выведены достаточные условия сбалансированности. Показано, что условие целочисленности вектора выпуска продукции существенно меняет свойства игры.

Введем необходимые обозначения: - множество неотрицательных целых чисел; - вклад игрока в максимальную коалицию; - множество перестановок ; , , ; - множество Вебера, где ; - множество дележей; - множество двойственных дележей; - С-ядро; - СС-ядро; . Очевидно , для любой игры .

Производственная игра определяется задачами линейного программирования (1), в которых вторая и третья группа ограничений отсутствуют, - производственная программа, - характеристический вектор коалиции . Моделируется ситуация, в которой каждый из игроков имеет ресурсы ( - количество видов ресурсов, - матрица ресурсов), необходимые для производства потребительских благ ( - количество типов продукции, - технологическая матрица). Продукция продается по рыночной цене ( - вектор цен). Объединяя ресурсы, агенты могут получить дополнительный доход. Максимальная стоимость продукции, которую можно произвести, используя ресурсы коалиции , равна

, , . (2)

Если производится продукция неделимого типа, то получаем игру с характеристической функцией , определенной задачами целочисленного линейного программирования, т.е. для любой коалиции

, , . (3)

Задача (2) является линейной релаксацией задачи (3), поэтому

, . (4)

будем называть целочисленной производственной игрой, а - релаксированной игрой. Для справедливы известные критерии непустоты множеств , и , но из-за целочисленности функции эти множества приобретают дополнительные свойства.

Утверждение 1. Множества , , и являются целочисленными многогранниками.

Доказательство. Для множества Вебера утверждение очевидно. Для многогранников и утверждение следует из формул, определяющих их вершины. Запишем систему, определяющую

; , ,.

Если система совместна, то имеет, по крайней мере, одну вершину. Пусть . Соответствующий базис состоит из строки (1,…,1) и (n-1)-ой строк, каждая из которых содержит единственный ненулевой элемент . Значит, . Из правила Крамера следует, что - целочисленный вектор.

Существование целых точек в множествах и , а также простота их нахождения, имеют особое значение в ситуациях, когда производится дефицитная или экспериментальная продукция неделимого типа и агенты заинтересованы в получении самой продукции, а не денежного эквивалента.

Основной концепцией решения кооперативной игры является С-ядро. В [6] получено достаточное условие сбалансированности инвестиционной игры с дискретными вкладами, справедливое также для целочисленной производственной игры

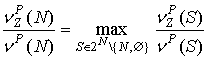. (5)

Для проверки условия (5) нужно решить задач целочисленного линейного программирования и столько же линейных задач. Задача целочисленного программирования является NP-сложной, поэтому актуален вывод условий непустоты С-ядра игры , требующих меньшего объема вычислений. Ниже приведены два таких условия.

Утверждение 2. Пусть , где - множество оптимальных решений задачи линейного программирования

, , . (6)

Если , то .

Доказательство. Возьмем . Тогда . Известно [2], что для любой производственной игры , . Из следует, что для любой коалиции , и . Значит, . ‚

Утверждение 3. Пусть и - вспомогательная игра с характеристической функцией

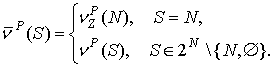
Если , то и .

Доказательство. Предположим, что - сбалансированная игра и . Из и (4) следует, что удовлетворяет ограничениям, определяющим С-ядро игры . Значит, . ‚

Утверждения 2-3 позволяют выделить подмножество дележей, принадлежащих С-ядру игры , без вычисления всех значений функции . Для проверки условия из утверждения 2 нужно решить одну целочисленную и одну линейную задачу. Если условие выполняется, то для параметрического описания множества нужно найти все оптимальные опорные решения задачи линейного программирования (6). Эта проблема решается с помощью существующих высокопроизводительных программ [7]. Условие из утверждения 3 требует решения одной целочисленной задачу (вычисление ) и линейных задач (вычисление , ), а также и проверки совместности линейной системы

.

Пример. Рассмотрим производственную ситуацию, в которой , , , , , 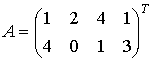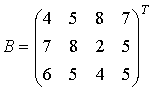. Задача, определяющая целочисленную производственную игру , и векторы ресурсов коалиций имеют вид

Значения функций , и оптимальные векторы выпуска продукции приведены в таблице 1. Игра не удовлетворяет достаточному условию сбалансированности (5), т.к.

,

а также условиям из утверждений 2-3. Тем не менее, целочисленная игра имеет непустое С-ядро (см. таблицу 2), не пересекающееся с С-ядром релаксированной игры, которое состоит из единственного дележа и совпадает с множеством . Кроме того, , т.е. в данной ситуации отличие игр и настолько существенно, что не только их С-ядра, но и множества дележей не пересекаются. Представляют также интерес соотношения между множествами дележей и С-ядрами 0-нормализованных игр , . Известно, что при 0-нормализации получается стратегически эквивалентная игра и С-ядро инвариантно относительно такого преобразования. После 0-нормализации вес максимальной коалиции равен дополнительному доходу от кооперации. Таблица 2 показывает, что множество дележей 0-нормализованной релаксированной игры содержится в множестве дележей 0-нормализованной целочисленной игры . Аналогичное включение справедливо для С-ядер .

Таблица 1

Производственные игры и оптимальные планы выпуска продукции

Целочисленная игра
Коалиция
	18	8	9	26	34	24	43
Вектор выпуска
	0	0	0	0	7	7	8
Релаксированная игра
Вектор выпуска
	0	0	0		0

Примечательно также, что 0-нормализация меняет статус игроков, причем один и тот же агент имеет разную "силу" в играх и . В игре единственным вето-игроком является агент 3, а в "право вето" имеет только агент 2. Еще одна особенность этого примера состоит в том, что (0,1)-форма релаксированной игры является также (0,1)-формой инвестиционной игры ([6], стр. 8) с тремя инвесторами (начальные капиталы: 60, 40, 40 д.е.) и двумя инвестиционными проектами (банковский депозит и дискретный вклад в производственный процесс).

Таблица 2

Множества дележей и С-ядра производственных игр

	Вершины множества дележей	Вершины С-ядра
	, ,	, , ,
	,,	, , ,
	, ,
	, ,

Литература:

1. Kalai E., Zemel E. Totally Balanced Games and Games of Flows // Math. Oper. Res. 1982. V. 7. P. 476-478.

2. Owen G. On the Core of Linear Production Games // Math. Programming. 1975. V. 9. P. 358-370.

3. Borm P., De Waegenaere1 A., Rafels C., Suijs J., Tijs S., Timmer J. Cooperation in capital deposit // OR Spektrum. 2001. V. 23. P. 265-281.

4. Gamble A.B., Pazgal A.I. A linear programming framework for network games // Discussion paper № 1119. Northwestern University. 1995. P. 1-27.

5. Tamir A. On the Core of Cost Allocation Games Defined on Location Problems // Transportation Science. 1993. V. 27. № 1. P. 81-86.

6. Waegenaere A.M.B., Suijs J.P.M., Tijs S.H. Stable profit sharing in cooperative investments // OR Spectrum. 2005. V. 27. №1. P 85-93.

7. Lrs Home Page: http://cgm.cs.mcgill.ca/~avis/C/lrs.html.