Економічні науки/8. Математичні моделі в економіці

К.ф.-м.н. Готинчан І.З., * ст. викл. Готинчан Г.І.^**

*Чернівецький торговельно-економічний інститут КНТЕУ, Україна

**Чернівецький факультет НТУ «ХПІ», Україна

Комп’ютерна реалізація математичної моделі динаміки промислового підприємства за участю зовнішніх інвестицій із запізненням як форми державної підтримки

Стаття присвячена комп’ютерній реалізації знаходження розв’язку математичної моделі динаміки промислового підприємства за участю зовнішніх інвестицій із запізненням, як форми державної підтримки, за допомогою ітераційного методу Адамса 4-го порядку. Здійснено розробку програмного засобу в середовищі Delphi 7.0, за допомогою якого можна досліджувати динаміку основних виробничих фондів на підприємстві з врахуванням збурень та інвестицій із запізненням.

Розглянемо адаптовану до умов турбулентного середовища базову модель динаміки підприємства (1), що використовує зовнішні інвестиції, як форму державної підтримки, представлену С.Р. Хачатряном [1]:

, (1)

де ; - зовнішні інвестицї, - показник фондовіддачі; - вартість основних виробничих фондів; - доля питомої собівартості випуску продукції у вартісному виразі; - ставки оподаткування на обсяг випуску і прибуток відповідно; - доля чистого прибутку, яка відраховується на реінвестування, ; - коефіцієнт, що відображає долю реінвестованих засобів прибутку, які не мають пільг по оподаткуванню (не всі реінвестовані засоби звільняються від податків), та характеризує співвідношення загального і чистого прибутку підприємства, і оцінюваний статистично ; - зовнішні інвестиції, отримані підприємством; - величина зовнішніх збурень; - функція Хевісайда, причому узагальнена функція і

Дана модель є адаптованою до змін зовнішнього середовища шляхом введення у вираз (1) узагальненої функції , яка визначає появу збурень у момент часу і величини зовнішніх збурень , що впливають на основні виробничі фонди.

У залежності від задання динаміки інвестицій , яке відповідає одному із трьом стратегіям державної фінансової підтримки підприємництва

- стала з фіксованими об'ємами інвестицій для кожного періоду;

1) - зростаюча по лінійному закону з темпом зростання інвестицій ;

2) - зростаюча по нелінійному (експоненційному) закону з середнім темпом і з мінімальним рівнем гарантованої державної підтримки ( при ),

загальний розв’язок лінійного неоднорідного диференціального рівняння із сталими коефіцієнтами (1) побудовано та детально вивчено в роботі [1].

Проте економічний зміст змінних, що входять в одержані розв’язки, є різний і визначається вихідними даними моделей, що розглядаються в кожному випадку.

Розв’язок рівняння (1) для випадку

, (2)

не можна знайти у явному вигляді, тобто для такої ситуації, коли потік державних інвестицій, які надходять із запізненням, пропорційний динаміці основних фондів промислового підприємства з коефіцієнтом пропорційності β (0 <β <1). Іншими словами, в даному випадку реалізується наступна стратегія державної підтримки - чим більше підприємство, тим більше інвестицій йому виділяється.

Якщо в рівняння (1) підставити (2), то воно набуває вигляду

, (3)

за початковою умовою

. (4)

Рівняння (3) є диференціальним рівняння першого порядку із запізненням. Задача (3) – (4) є задачею Коші й доцільно розв’язувати її наближеними методами.

Знаходження розв’язку задачі (3) – (4) проводилось за алгоритмом побудови різнецевої схеми четвертого порядку (різнецевої схеми Адамса для задачі Коші) у вузлах , рівномірної сітки :

1) , ,

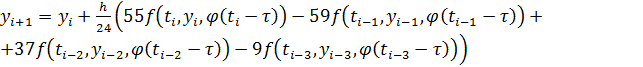якщо , де ;

2) , ,

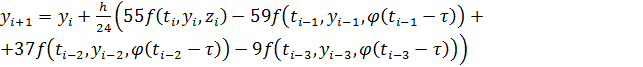якщо

3) , ,

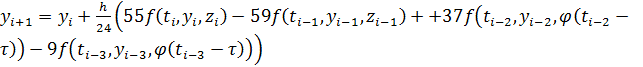якщо ,

4) , ,

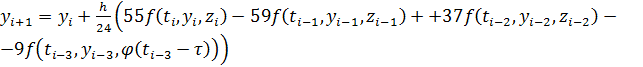якщо , ,

5) , ,

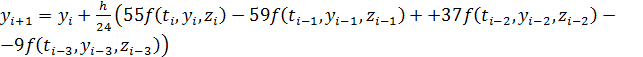якщо

Величини , знаходяться за наступним алгоритмом:

1) Знаходимо ;

2) знаходимо, використовуючи інтерполяційний многочлен Лагранжа, побудований по точках , , , , :

Різнецева схема була реалізована у середовищі Delphi 7.0.

Результати дослідження можуть бути застосовані для спостереження поведінки основних виробничих фондів на підприємстві з урахуванням збурень та інвестицій із запізненнями.

Література:

1. Хачатрян, С.Р. Методы и модели решения экономических задач: научно-методи-ческое пособие / С.Р. Хачатрян, М.В. Пинегина, В.П. Буянов. – М. : Экзамен, 2005. – 383 с.

2. Архангельський А.Я. Програмування в Delphi. Підручник з класичним версіями Delphi /А.Я. Архангельський. - М.: ТОВ «Біном-Пресс», 2006. - 1152 с.

3. Заусаев А.Ф. Разностные методы решения обыкновенных дифференциальных уравнений: Учеб. Пособ / А.Ф. Заусаев. - Самара: Самарский гос. техн. ун-т, 2010. - 100 с.