Математика. Дифференциальные и интегральные уравнения

К.пед.н. Башкирова И.В., к.ф.-м.н. Карнишин С.Г.

Пермский военный институт внутренних войск МВД России

(ПВИ ВВ МВД России), Россия

Устойчивость периодического уравнения

с последействием

Для периодического уравнения с последействием рассматривается вопрос о связи экспоненциальной оценки матрицы Коши и разрешимостью периодических краевых задач.

Рассмотрим уравнение третьего порядка с последействием

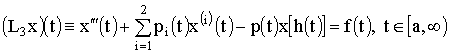(1)

при условии однозначной разрешимости задачи Коши и периодичности параметров уравнения:

;

где - первая неподвижная точка функции h(t).

Известно следующее утверждение о существовании экспоненциальной оценки матрицы Коши и фундаментальной матрицы уравнения (1).

Теорема 1. Если спектральный радиус матрицы монодромии меньше единицы, то существуют :

(2)

Собственные значения матрицы монодромии , то есть корни характеристического уравнения (так называемого уравнения Флоке-Ляпунова) (здесь - единичная матрица), называются мультипликаторами уравнения (1). Известно, что каждому мультипликатору уравнения (1) соответствует нетривиальное решение (1), удовлетворяющее условию , причём это решение имеет представление:

, если , где .

Введём в рассмотрение следующую вспомогательную краевую задачу:

(3)

Имеет место следующее утверждение.

Теорема 2. Задача (3) имеет единственное решение тогда и только тогда, когда число не является мультипликатором уравнения (1).

Будем говорить, что выполняется условие , если для любого краевая задача

(4)

однозначно разрешима.

Лемма 1. Если выполняется условие , то уравнение (1) не имеет отрицательных мультипликаторов.

Введём в рассмотрение ещё два условия:

: для любого и для любого существует функция Грина задачи

(5)

: для любого существует функция Грина задачи

(6)

Лемма 2. Для того чтобы положительное число не являлось мультипликатором уравнения (1), необходимо, а при выполнении условий и достаточно, чтобы существовала функция :

1. ;

2. - абсолютно непрерывна на ;

3. , где на .

Обозначим далее и построим следующий многочлен:

. (7)

Легко видеть, что если хотя бы один из коэффициентов не равен нулю (тождественно), то многочлен (7) имеет единственный положительный корень . При этом , если , если , где - положительный корень многочлена (7).

Теорема 3. Пусть уравнение (1) имеет положительные мультипликаторы, - положительный корень многочлена . Для того, чтобы действительные мультипликаторы уравнения (1) удовлетворяли неравенству , необходимо, а при выполнении условий и (V₃) достаточно, чтобы для каждого 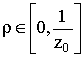существовала функция такая, что

1. ;

2. - абсолютно непрерывна на ;

3. для любого 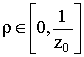функция удовлетворяет неравенству , причём на .

Следствие. Пусть выполнены условия и . Если

при всех 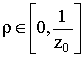и пусть для любого фиксированного , то действительные мультипликаторы уравнения (1) удовлетворяют неравенству .

Будем говорить, что выполнено условие, если почти для всех в промежутке любое нетривиальное решение уравнения (1) имеет не более двух нулей.

Лемма 3. Если и на выполнено условие, то имеет место неравенство:

,

где - вронскиан уравнения (1).

Следствие. Если 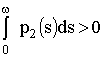, то .

Теорема 4. Пусть выполнены условия , и . Кроме того, пусть

1) для каждого 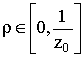существует -периодическая функция с абсолютно непрерывной второй производной такая, что при каждом 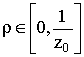функция удовлетворяет неравенству на ;

2) для каждого 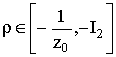, где 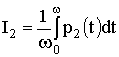существует -периодическая функция с абсолютно непрерывной второй производной такая, что при каждом 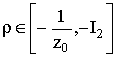функция на .

Тогда для матрицы Коши уравнения (1) имеет место экспоненциальная оценка (2).

Следствие. Если выполнены условия , и , то

1) при всех ;

2) при всех ;

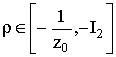причём для любого фиксированного и .