Ст. преп. Дзогий И.В.

Брянский государственный университет имени ак. И.Г. Петровского, Россия

Обобщение классической теоремы Фрагмена – Линделефа для классов Привалова И.И.

Теорема Фрагмена – Линделефа основана на классическом свойстве максимума аналитических функций, т. е. если аналитическая функция не превосходит постоянной на границе ограниченной области, то она не превосходит постоянной и внутри этой области, и представляет собой обобщение этого свойства на области, уходящей в бесконечность (см. [2]).

Большую роль в комплексном анализе играют различные оценки модуля аналитической функции внутри правой полуплоскости, если дана соответствующая оценка на границе (мнимая ось) или даже части границы этой полуплоскости. Похожая задача была сформулирована Масляковым Ю.И. и опубликована в журнале «Математический сборник» в 1966 году, где, как известно, вместо роста модуля аналитической функции в правой полуплоскости оценивалось его убывание, исходя из его убывания на мнимой оси (см. [5]).

Также подобные оценки возникают при рассмотрении различных вопросов анализа, таких как локализуемость замкнутых идеалов аналитических функций или, например, теорема Рисса-Торина в теории операторов.

Теорема 1. (Фрагмена - Линделефа) (см. [4]).

Пусть - угол на комплексной плоскости раствора 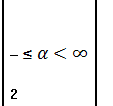с вершиной в начале координат, а − функция, аналитическая внутри и на границе . Предположим, что на границе выполняется

, (1)

а всюду в выполняется

, , (2)

где . Тогда всюду в выполняется неравенство (1).

Теорема 2. (Фрагмена - Линделефа) (см. [4]).

Утверждение теоремы 1 сохраняет силу, если условие (2) заменить более слабым:

, , (3)

В частности, если - полуплоскость, и на ее границе выполняется (1), а всюду в выполняется

, , (4)

то (1) справедливо всюду в .

Оказалось, что оценки такого рода справедливы не только для аналитических непрерывных вплоть до границы и ограниченных функций, но и для функций из классов Привалова И.И., где на границе оценка "всюду" заменяется на оценку "почти всюду" и существенно расширяется класс функций, где справедлив такой результат (см. [8]).

Приваловым И.И. был рассмотрен класс аналитических в единичном круге функций , удовлетворяющих условию:

, , где (см. [6]). Обозначим этот класс через .

Рассмотрим такой класс в случае правой полуплоскости . Пусть − класс аналитических в правой полуплоскости функций , удовлетворяющих условиям:

1) , , где

2) .

При , класс 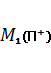− это известный класс Неванлинны (см. [1]).

Теорема 3.

Пусть функция, и на границе почти всюду удовлетворяет условию

, (5)

где − положительная возрастающая непрерывная функция, выпукла вниз при t0, и . Тогда всюду в справедлива оценка

. (6)

Литература:

1. Гарнетт Дж. Ограниченные аналитические функции. / Дж. Гарнет. – М.: Мир, 1984.

2. Гельфанд И.М., Шилов Г.Е. Пространства основных и обобщенных функций. / И.М. Гельфанд, Г.Е. Шилов. – М.: 1958.

3. Евграфов М.А. Асимптотические оценки и целые функции / М.А. Евграфов.–М.: Физматгиз, 1962.

4. Линник Ю.В., Островский И.В. Разложения случайных величин и векторов. / Ю.В. Линник, И.В. Островский. – М.: Наука, 1972.

5. Масляков Ю.И. Об убывании функций,аналитических в полуплоскости / Ю.И. Масляков // Математический сборник. 1966. – Т. 69,№4. – С. 658 - 662.

6. Привалов И.И. Граничные значения однозначных аналитических функций / И.И. Привалов. – Москва –Ленинград: Гостехиздат, 1950.

7. Шамоян Ф.А. Диагональное отображение и вопросы представления в анизотропных пространствах голоморфных в полидиске функций / Ф.А.Шамоян // Сиб. мат. журн. 1990. – Т. 31, № 2. – С. 197 - 215.

8. Щербенко И.В., Яшина Е.В. О некоторых оценках в одном пространстве аналитических в полуплоскости функций / И.В. Щербенко, Е.В.Яшина // Материалы Воронежской весенней математический школы. Современные методы теории краевых задач. – Воронеж: 2003. – С. 161.

9. Шамоян Ф.А., Щербенко И.В. О некоторых оценках в одном пространстве аналитических в прямолинейной полосе функций / И.В.Щербенко, Ф.А. Шамоян // Сборник студенческих научных работ БГУ. Тезисы докладов.– Брянск: Издательство БГУ, 2003. – С. 12.