Математика/ 3

К.т.н. Шепетюк Б.Д., д.ф.-м.н. Нестерук І.Г.

Чернівецький національний університет імені Юрія Федьковича, Чернівці, Інститут гідромеханіки НАН України, Київ, Україна

ПРОГРАМНІ ЗАСОБИ ОЦІНКИ ВПЛИВУ ВЕНТИЛЯЦІЇ НА ФОРМУ ТОНКИХ ОСЕСИМЕТРИЧНИХ КАВЕРН

Для зменшення опору корпусів високошвидкісних підводних апаратів широко використовується суперкавітаційний режим обтікання [1], що дозволяє значно знизити опір тертя через зменшення площі контакту з водою. Разом з тим, для суперкавітації характерні високі значення опору тиску. Баланс цих двох тенденцій був проаналізований в [2-4] для тонких осесиметричних тіл, які можна вважати першим наближенням для форми корпусів.

Результати робіт [2-4] свідчать, що об’ємний коефіцієнт опору суперкавітуючих тіл може бути значно зменшений при дуже малих числах кавітації

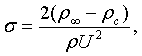₍₁₎

де ρ–густина води; U–поточна швидкiсть тiла; – тиск у водi далеко вiд перерiзу початку каверни на глибинi його руху; –тиск в кавернi.

Відповідно до формули (1) досягнути дуже малих чисел кавітації можна за рахунок збільшення швидкості руху тіла або шляхом підвищення тиску газу в каверні з використання піддуву (так звана штучна кавітація).

Другий шлях передбачає більш чи менш інтенсивну вентиляцію газом, що рухається у вузькому кільцевому каналі між поверхнями тіла та каверни (рис.1.).

Дана робота присвячена розробці засобів програмного моделювання впливу течій газу у вузькому каналі на форму тонкої (видовженої в напрямку руху) осесиметричної каверни.

Fig1

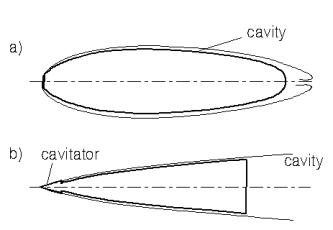
Рис. 1. Схеми суперкавітаційного обтікання з вузькими каналами між корпусом тіла та поверхнею каверни

Основні рівняння для форми штучної тонкої осесиметричної каверни

Аналіз задач суперкавітації ускладнюється відсутністю точних розв’язків, тривимірним та нестаціонарним характером течії. Останнім часом широко використовуються чисельне моделювання таких течій з використанням рівняннь Нав’є-Стокса та фазових переходів. Зазначені моделі містять однак велику кількість емпіричних параметрів, значення яких слід підбирати шляхом порівняння з експериментом, що робить їх не дуже надійними, особливо при зміні характеристик потоку, оскільки може виникнути потреба в уточнені параметрів, закладених в розрахунок.

Разом з тим, в деяких випадках горизонтального високошвидкісного руху можна знехтувати впливом сили тяжіння та вважати режим обтікання квазістаціонарним. Якщо обмежитись саме такими течіями та випадком тонких кавітаторів і утворених ними каверн, то можна користуватись отриманим в [6] рівнянням першого наближення, що дає дуже простий зв’язок між радіусом осесиметричної каверни R(x)та коефіцієнтом тиску С_р(х)=-

де - малий параметр, відношення максимального радіуса системи каверна-кавітатор до її довжини.

Через велику різницю в густинах води і газів, що заповнюють каверну, тиск в каверні ічисло кавітації в абсолютній більшості робіт вважають сталими (незалежними від координати х). Але у випадку інтенсивного піддуву у вузькому кільцевому каналі ця умова може порушуватись. Для оцінки зміни тиску у потоці газу скористаємось найпростішою моделлю одновимірної течії ідеального нестисливого газу. Тоді рівняння Бернулі та нерозривності можна записати у вигляді:

де - густина газу, що використовується для піддуву (вважається сталою); V- його поточна швидкість; Q- об’ємне витрачання газу; - швидкість, тиск газу та радіус каверни в перерізі початку каверни х = 0; - поточний та початковий радіуси тіла ( рис.2).

Fig2

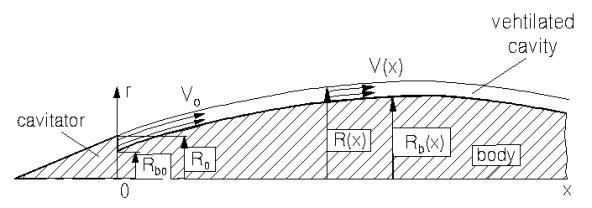
Рис. 2. Схема суперкавітаційного обтікання з інтенсивним піддувом

З рівнянь (3), (4) випливає, що тиск в каверні залежить від координати х за законом

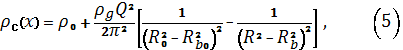
підстановка якого у співвідношення (2) дає таке диференціальне рівняння для радіуса каверни:

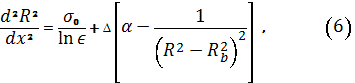
в якому всі довжини віднесені до радіуса каверни в точці її початку ,а сталі параметри та визначаються формулами

Якщо вентиляція відсутня(∆=0), то рівняння(6) збігається з рівнянням першого наближення [6] для форми тонкої осесиметричної стаціонарної каверни з числом кавітації, його розв’язок для стандартних початкових умов в точці сходу каверни х = 0

R =1,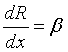, (10)

має вигляд

У випадку каверни з піддувом газу потрібно розв’язувати більш складне нелінійне диференціальне рівняння (6), аналіз якого показує, що вентиляція може значно змінити форму каверни не лише при достатньо великих значеннях витрачання газу (параметра ∆), але і у випадку дуже малих величин (R-R_b). Зокрема, якщо (R-R_b) прямує до нуля, то з рівняння (6) випливає, що каверна відповідає числу кавітації, значно більшому, ніж тобто її розміри повинні зменшуватись порівняно з невентильованою каверною (11). Даний факт, звичайно, не суперечить фізичним уявленням про вплив вентиляції.

Опис інтерфейсу програмного комплексу

Результатом роботи є програмне забезпечення для дослідження впливу течiй газу у вузькому каналi на форму тонкої (видовженої в напрямку руху) осесиметричної каверни[7].

Після запуску програми перед користувачем відкриється головне вікно програми (рис 3).

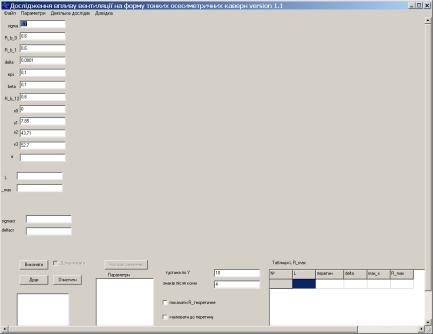
Рис. 3. Головне вікно програми

Користувачеві необхідно задати ряд вхідних даних, які вводяться вручну у відповідні поля (рис 4.) або читаються з файлу, при виборі пункту меню “Файл - Відкрити” (рис 5.).

Рис. 4. Введення початкових даних Рис. 5. Пункт меню “Файл”

Задаючи величини R_b_0, R_b_1, R_b_12 та відповідні значення x0, x1, x2, x3 користувач має можливість задавати циліндричне тіло складної конфігурації. При встановленні галочки в полі “нейтральне тіло” та натискані кнопки “Вибір форми тіла” є можливість моделювати ситуації для нейтрального тіла. Після того, як користувач задав усі необхідні початкові дані, він може отримати результат обчислень натиснувши на кнопку “Виконати”. Результатом цього є виведення на екран графіку розв’язку (рис 6.).

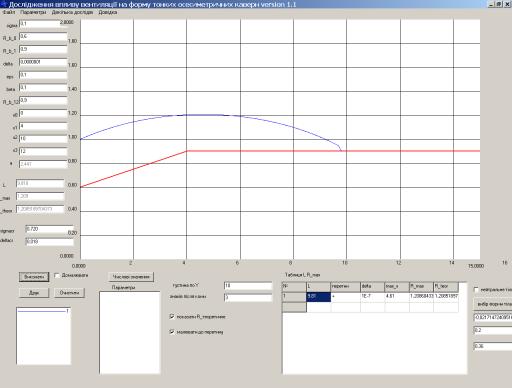
Рис. 6. Графік для циліндричного тіла складної конфігурації

Якщо користувач при натисненні на кнопку “Виконати” поставить галочку у полі “Домалювати”, то нові результати виведуться разом із тими, що уже були виведені раніше (рис 7.).

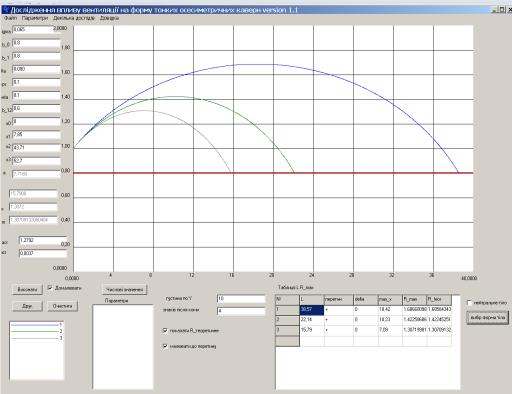
Рис. 7. Декілька графіків (приклад циліндричного тіла)

Параметри кожного з виведених графіків виводяться у поле “Графіки”. Щоб отримати детальнішу інформацію про якийсь графік необхідно вибрати його зі списку. Інформація виведеться у поле “Параметри” (рис 8.).

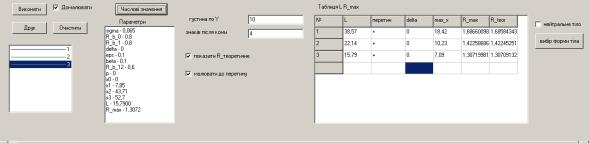
Рис. 8. Параметри побудованих графіків

Також по кожному графіку користувач може отримати числові значення натиснувши кнопку “Числові значення”. Перед користувачем відкриється форма, у якій буде виведено розв’язок задачі не у графічному вигляді, а у числовому (рис 9.).

При натисненні на кнопку “Друк” усі графіки разом зі своїми параметрами(які обираються на вибір) зберігаються у заданий користувачем графічний файл.

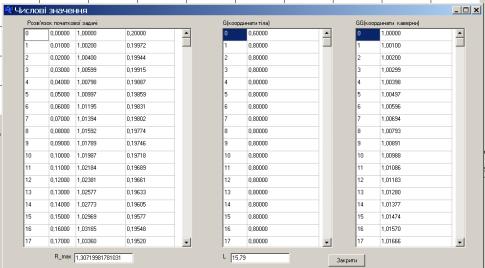
Рис. 9. Числові значення розв’язків

При виборі пункту меню “Параметри – Параметри обчислень” перед користувачем відкриється форма, у якій він може задати наступні параметри: точність обчислення, крайня права точка відрізку і коефіцієнт кількості точок. При виборі пункту меню “Параметри – Параметри графіку” перед користувачем відкриється форма, у якій він може задати або змінити граничні значення графіку(рис 10).

$E:\курсова\31_05_13\tabl\paramgraph.bmp$

$E:\курсова\31_05_13\tabl\paramob4.bmp$

Рис. 10. Параметри обчислень

При виборі пункту меню “Декілька дослідів” користувач може повести декілька дослідів по параметрах delta(вентиляція) чи sigma(-число кавітації). Перед користувачем з’явиться вікно, в якому він може задати клька дослідів списком чи діапазоном (рис.11).

Рис. 11. Декілька дослідів заданих діапазоном

Користувач має змогу зберегти усі вхідні дані, параметри обчислень і параметри графіку у файл, вибравши пункт меню “Файл - Зберегти”.

Розроблене програмне забезпечення дозволяє автоматизувати процес моделювання впливу вентиляції на форму тонких осесиметричних каверн.

Література:

1. Логвинович Г.В. Гидродинамика течений со свободными границами К.Наук. думка.1969. -208с.

2. Нестерук I. Г. Зменшення опору видовжених осесиметричних високошвидкiсних тiл.// Прикладна гiдромеханiка. 2009 Т. 11 (83), N 2. С. 55 – 67.

3. Нестерук I. Г., Савченко Ю.М., Семененко В.М. Оптимiзацiя дальностi для суперкавiтацiйного руху за iнерцiєю //Доповiдi НАН України. 2006. N8.С.57-66.

4. Нестерук I. Г. Задачi оптимiзацi дальностi суперкавiтацiйного руху за iнер-цiєю з фiксованою початковою глибиною //Прикладна гiдромеханiка. 2008 Т. 10 (82), N 3. С.64-75.

5. Перник А. Д. Проблемы кавитации. 2-ое изд. Л.: Судостроение, 1966. 435с.

6. Нестерук И.Г. К вопросу о форме тонкой осесимметричной каверны в весомой жидкости //Известия АН СССР, МЖГ.- 1979.- N 6. –С. 133-136.

7. Манова З.І,, Нестерук І.Г., Шепетюк Б.Д.. Оцінки впливу вентиляції на форму тонких осесиметричних каверн // Прикладна гідромеханіка. – 2011. Т.13 (85), № 2. – с. 44-50.