УДК 539.3

СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ БАЛКИ ТИМОШЕНКО

С. Абдурахманов, ТашГТУ,

Ж.С Еркишева, М . Д. Кошанова, МКТУ им. Ясави

С увеличением размеров и скоростей современных машин в инженерных расчетах становится все более важным решение задач, связанных с колебаниями. Хорошо известно, что только на основе теории колебаний могут быть полностью выяснены такие практически важные проблемы, как уравновешивание машин, крутильные колебания валов и зубчатых передач, колебания турбинных лопаток и турбинных дисков, колебания рельсового пути и мостов под действием движущихся грузов, колебания фундаментов. Лишь при помощи этой теории можно установить наиболее удачные пропорции конструкций летательных аппаратов.

В работах [1,2] рассматривались динамические задачи упругих балок с учетом инерции вращения и поперечного сдвига. Однако применяемые материалы в настоящее время в технике в той или иной мере характеризуется вязкими свойствами, в связи с чем упругая аппроксимация свойств материала не всегда допустима.

В настоящей работе рассматриваются задачи о свободном и вынужденном колебания вязкоупругой балки Тимошенко с учетом поперечного сдвига и инерции вращения. При реальном учета физико-механической свойств материала строится математическая модель оставленной задачи. Математической моделью поставленной задачи является интегро-дифференциальное уравнение в частных производных с соответствующими начальными и граничными условиями. Полученные интегро-дифференциальное уравнение в частных производных с помощью метода Бубнова-Галеркина сводится к решению систем обыкновенных интегро-дифференциальных уравнений с переменными коэффициентами относительно функции времени. Интегрирование уравнений было проведено численным методом, предложенном в работах [3] На основе этого метода разработаны алгоритмы численного решения задач о колебаниях и динамической устойчивости вязкоупругой балки с учетом сдвига и инерции вращения.

Рассмотрим поперечные колебания вязкоупругой балки, основанной на модели С.П. Тимошенко [1, 2]. Физическое соотношение между напряжениями и деформациями примем в виде

где, - модуль упругости; - интегральный оператор с ядром релаксации

Обозначим через угол наклона кривой прогибов, а через угол поперечного сдвига. Тогда связь между ними аналогично [75, 109] описывается уравнением

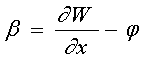
Связь между деформацией и углом поворота запишем в виде:

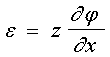
Тогда для изгибающего момента М и поперечной силы Q будем иметь выражения

(1)

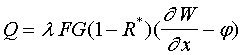
где l-коэффициент, зависящий от формы поперечного сечения балки; F площадь поперечного сечения G-модуль сдвига; J-момент инерции.

Подставляя (1) в уравнения.

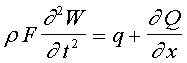
получим

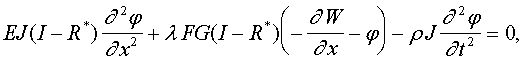
(2)

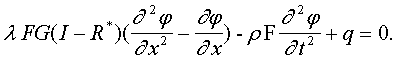
Где r -плотность материала балки.

Пусть стержень имеет начальный прогиб , Тогда уравнение (2) с учетом начальных прогибов имеет вид:

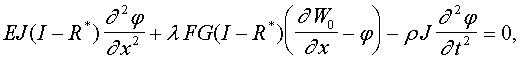
(3)

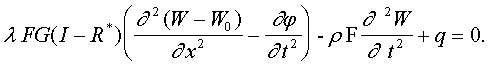
Введем безразмерные параметры: где, - частота основного тона колебаний шарнирно опертого упругого стержня. - радиус инерции сечение.

Решение систем интегро-дифференциальных уравнений полученные выше при различных граничных условиях и при наличии слабо сингулярных ядер наследственности представляет значительные математические трудности. Поэтому естественным способом решения этих систем является дискретизация по пространственным переменным и получение систем обыкновенных интегро-дифференциальных уравнений относительно искомых функций времени. В настоящей работе получен систем обыкновенных интегро-дифференциальных уравнений применен методом Бубнова-Галеркина. Переходя к безразмерным параметрам и проводя несложные математические преобразование получим:

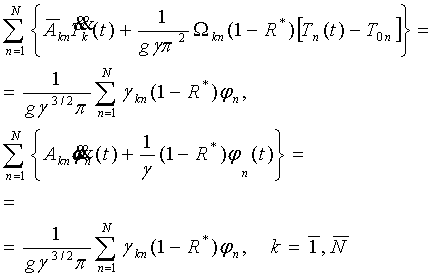(5)

В [3] для решение систем интегро-дифференциальных уравнений предложен численный метод, основанный на использовании квадратурных формул. Этот метод распространим для систем вида (5)

Пологая i = 1,2, ... и земеняя интегралы некоторымы квадратурными формулами, для вычисления значений

получим следующие систему линейных алгебраических уравнений.

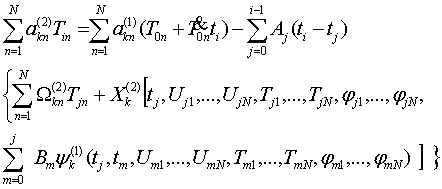
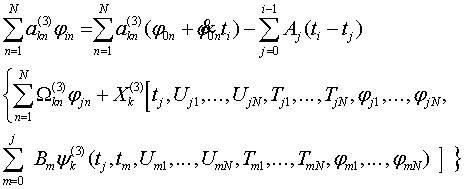
где -числовые коэффициенты, принимающие различные значения в зависимости от использованных квадратурных формул.Полученная систем решается методом Гаусса. р

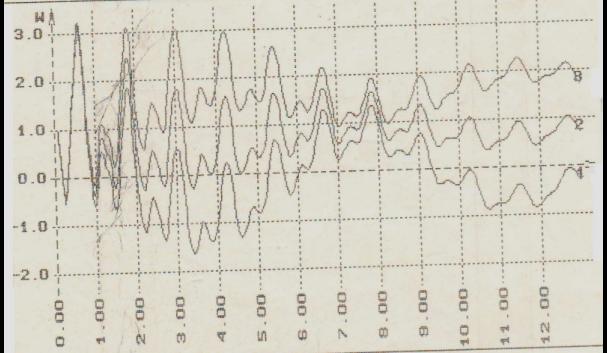
На рисунке представлен график колебании балки с учетом инерции вращения и сдвига (кривая 1) только инерции вращения (кривая 2) без учета инерции вращения и сдвига (кривая 3)

Литература

1. Тимошенко С.П., Янг Д.Х., Уивер У. Колебания в инженерном деле. М. Машиностроение. 1985, 472 с.
2. Тимошенко С.П. Курс теории упругости. Киев, Наукова думка, 1972, 501 с.
3. Бадалов Ф.Б. Методы решения интегральных и интегро-дифференциальных уравнений наследственной теории вязкоупругости. Ташкент, Мехнат, 1987 г., 269 с.