Комолов В.М., к. физ.-мат. Латынин Ю.М.

      Украинская инженерно-педагогическая академия. г. Харьков

 

Обобщенная формула тангенсов: Примеры

применения

           

Введение. В работе [1] формула тангенсов для плоского  косоугольного треугольника со  сторонами и  противолежащими им углами :

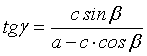                                                             при  а > с                  (1)             

преобразована в эквивалентную, и  для угла   получено аналитическое  представление:                              (2)

 где  а и с стороны треугольника, образующие угол  .

Цель  работы,  Получение обобщенного варианта  формулы тангенсов  и ее приложения к теории  тригонометрических и гиперболических функций.

Основная часть. Пусть в  плоскости комплексного переменного z=x+iy заданы z1=a; z2=b∙eiα , причем a, b >0. В соответствии с обобщенными теоремами сложения [2] модуль |W| и аргумент θ комплексного числа W =z1+z2 определяют соотношения:

                   W=a+beiα=(a+b∙cosα)+i∙b∙sinα=|W|∙еiθ,                          (3)

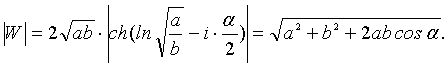                                 (4)

                         (5) 

       Так как   tg θ  = , то                       

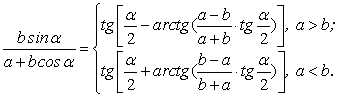                                                      (6)

  Для разности z1 и z2, т.е. W1 = z1−z2 = (a − b∙cosα) − i∙b∙sinα= |W1|∙eiθ1, модуль и аргумент соответственно равны:

           ,                (7)

            argW1 =θ1= 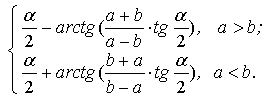                                       (8)

Аналогично, 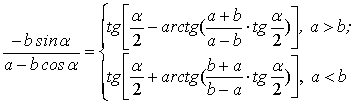                                (9)

Унифицируем формулы (6) и (9), чтобы их использовать в дальнейшем. Введем параметр η=a/b:             (10)

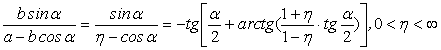                                   (11)

Применение формулы тангенсов в форме (10), (11) позволяет получить ряд новых соотношений в теории тригонометрических функций. Приведем  примеры.

1. Получим формулы  для суммы и разности двух аргументов тангенса, т.е. tg(α±β). Представим сначала тангенс как сумму четырех слагаемых:

                      tg(α+β)=∙tg(α+β) + ∙tg(α−β) +∙tg(α+β) − ∙tg(α−β).            (12)

 Для первой пары слагаемых

         ∙tg(α+β) + ∙tg(α−β) =   .              (13)

Аналогично преобразуется вторая пара слагаемых в (12):

            ∙tg(α+β) − ∙tg(α−β) = ∙tg(α+β) + ∙tg(β −α)=           (14)

Формула (13) превращается в (14) и наоборот при замене переменных α↔β. Правую часть (13) с учетом (10) представим так:

                   (15)

Аналогично, для правой части  (14) имеем:

                     (16)

Таким образом, справедливо следующее равенство: .(17)

В элементарной тригонометрии известно другое представление для тангенса суммы двух углов α и β:     tg(α+β)=.

Эту несимметричную формулу можно свести к симметричной (17):                                   

                                            tg(α+β)==

 

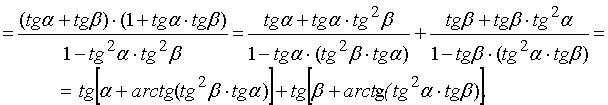
Последняя совпадает с (17). Для тангенса разности 2-х углов  воспользуемся заменой  β→(−βI). Получим формулу, аналогичную (17):

  tg(α−βI)=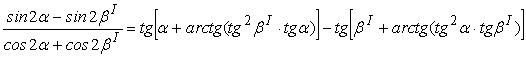.18)

2. Применим (10) для суммы и разности  двух тангенсов: tgx±tgy. Известно:

            tgx±tgy=.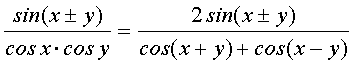

С учетом того, что η= cos(x−y), для  суммы тангенсов получим:

              =

=.

Окончательно,    tgx+tgy = 2∙.               (19)

Для разности двух функций  тангенса:

                        tgx−tgy = 2∙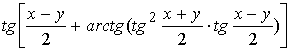           (20)

 В частном случае, когда y=0, из (19),(20):

                                                                             (21)

Положив в (17) сначала x=y=xI/2, а затем и  x=y=xI, получим  соотношения,  которые совпадают с (21):

                                   ;

       .

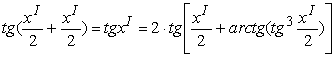3. Для  гиперболических функций действительного переменного учтем, что               

                        tg(iz)=i∙th(z);    Arctg(iz) = i∙Arth(z)+2kπ,  k=0,1,2...                 (22)

и  получим аналоги вышеприведенных формул. Из (19) и (20):

                                 (23)

  Аналогично, из (17) и (18) имеем:              

                th(x±y)=th[ x−Arth(th2y∙ thx)]± th[ y−Arth(th2x∙thy)]                 (24)   

       4. Получим представление для действительной и мнимой частей тангенса  tg(z), th(z)  при комплексном характере аргумента: z=x+iy  . Принимая во внимание  (22), из (17) имеем:

      tgz= tg(x+iy)= tg[x−arctg(th2y∙tgx)]+i∙th[y+Arth(tg2x∙thy)];         (25)

            th(x±iy)= th[x+Arth(tg2y∙thx)]± i∙tg[y−arctg(th2x∙tgy)].            (26)

       5. Применим изложенную выше методику, чтобы получить аналогичные соотношения для функции котангенса: ctg(α+β), ctgx + ctgy  и др. Представим, как и в  (12), функцию ctg(α+β) в виде суммы 4-х слагаемых:

          сtg(α+β)=сtg(α+β) + сtg(α−β) +∙сtg(α+β) − ∙сtg(α−β).             

Учтем, что       ∙сtg(α+β) + ∙сtg(α−β)=  ,

                          ∙сtg(α+β) − ∙сtg(α−β)=.

В итоге получим        сtg(α+β) =−.                        (27)

После применения (11) и элементарных преобразований:

    .            (28)

 Заменив β→ − β, получим соотношение для котангенса разности двух углов:

             (29)

 Известное из тригонометрии представление сtg(α+β)=  преобразуется аналогично:

          

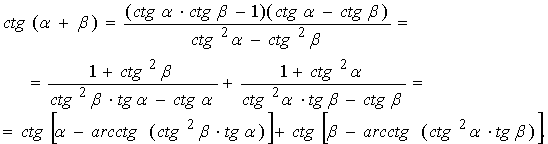
Последнее соотношение  совпадает с (28).

    6. Рассмотрим сумму и разность двух функций котангенса ctgx±ctgy . Извест-   но:                            ctgx+ctgy=.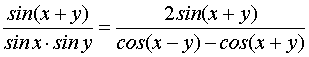

При сопоставлении этого выражения с (11),  η = cos(x−y):

                  ,    

                  ctgx+ctgy=−2∙                    (30)

 Далее используем равенство, которое вытекает из вышеприведенных формул:              

                                   ,                             (31)

                            где  z = ctg2[(x−y)/2]∙ tg [(x+y)/2],  γ=(x+y)/2.

Тогда     ctgx+ctgy=2∙∙                       (32)

 Для разности функций котангенсов

                  сtgx −ctgy=2∙∙                 (33)     

    7. Получим  аналоги формул для гиперболических функций  действительного переменного, учтя тождества:

                     i∙ctg(iz)=cth(z);  i∙Arcctg(iz)=Arcth(z).                                 (34)

Формулы (32) и (33) принимают следующий вид:

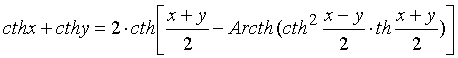           .                  (35)

 Аналогично из (28), (29)

      (36)

Получим новое представление ctg(z) и cth(z) при переходе в область комплексного переменного z=x+iy. Принимая во внимание (34), из (28), (29) имеем:

(37)

                     (38)

    8. Пусть заданы две величины:  Их сумма z=z1+z2= = где  θ есть аргумент комплексного числа z: θ= arg(z1+z2). Как показано в [2]:

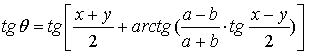                             .                                  (39)

 В тоже время                             

               .                (40)

Принимая во внимание соотношение (10), запишем:

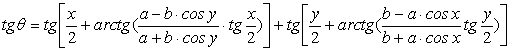                    (41)

Из сопоставления (40) и (41) вытекает  справедливость  соотношения:

 (42)

  Множители в круглых скобках, можно преобразовать  к следующему виду:

                               

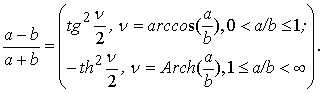
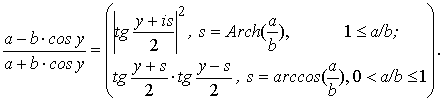                                   (43)

                  

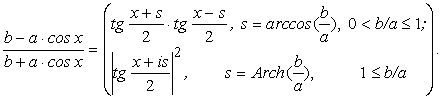
С учетом этих соотношений равенство (42) можно представить в более  компактном виде.

         Выводы: В работе продемонстрирована возможность  получения на основе обобщенной формулы тангенсов симметричной формы ряда соотношений  для тригонометрических и гиперболических функций.

Литература:

1.     Комолов В.М., Латынин Ю.М.  Об эквивалентности  ряда формул  плоского косоугольного треугольника. Materials of the X International scientific and practical conference «Proceedings of academic science»,-2014. Vol.6. Mathematics. Physics. Sheffield. Science  and Education LTD.- P.6-10.

2. Комолов В.М., Обобщение теорем сложения для тригонометрических функций. Materials of the X International scientific and practical conference «Modern european science»,-2014.Vol.15. Mathematics. Physics. Sheffield. Science  and Education LTD.- P.38-42.