Момотенко Д. О., Ладієва Л. Р.

Національний технічний університет України «КПІ», Україна

Оптимальна система керування процесу адсорбції

Представимо математичну модель адсорбції в канонічній формі з урахуван-ням математичних перетворень:

де ; ;; ; U – швидкість потоку; S – площа поперечного перерізу; τ – час; C – концентрація; ε – коефіцієнт масопередачі; β = (NuD)/d² – коефіцієнт зовнішнього масообміну; d – еквівалентний діаметр частинок; D – коефіцієнт нормальної дифузії; Nu – число Нуссельта.

із початковими та граничними умовами:

τ = 0; 0 ≤ x ≤ L; С = 0;

τ > 0; x = 0; С = С₀ = const.

Розв’язуємо задачу знаходження оптимального програмного керування.

В якості критерію оптимальності обрано квадратичний інтегральний критерій якості, що мінімізує відхилення концентрації адсорбтиву на виході від заданої

Необхідні умови оптимальності оптимальності:

гамільтоніан Н матиме наступний вигляд:

Спряжена система:

Умови трансверсальності:

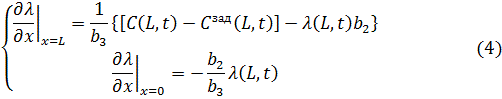
Похідна по керуванню дорівнює

Математичну модель та спряжену систему представили в дискретній формі

Для вирішення задачі пошуку оптимального програмного керування застосували градієнтну процедуру за таким алгоритмом:

1. Розв’язуємо математичну модель в прямому часі при постійному керуванні.

2. Розв’язуємо спряжену систему у зворотному часі.

3. Проводимо покращення керування:

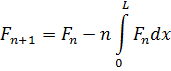
де , де – функція Хевісайда.

4. Повертаємось до пункту 1 з покращеним керуванням.

5. Алгоритм виконується доти доки не виконуватимуться умови збіжності.

Даний алгоритм був реалізований в математичному пакеті MathCad і отримано такі графіки:

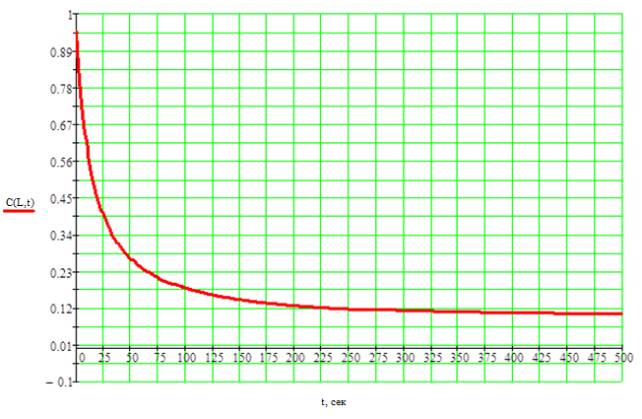
Рис 1 «Розв’язок математичної моделі в прямому часі при постійному векторі керування»

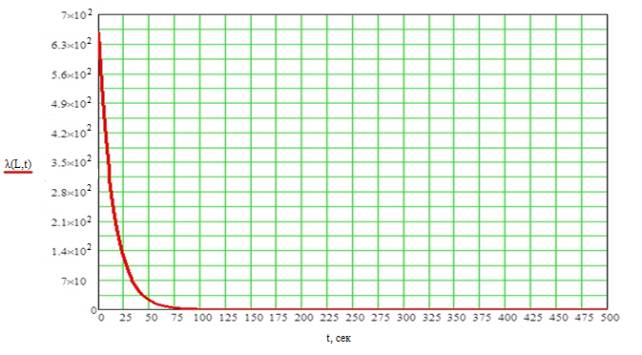
Рис 2 «Розв’язок спряженої системи в зворотньому часі»

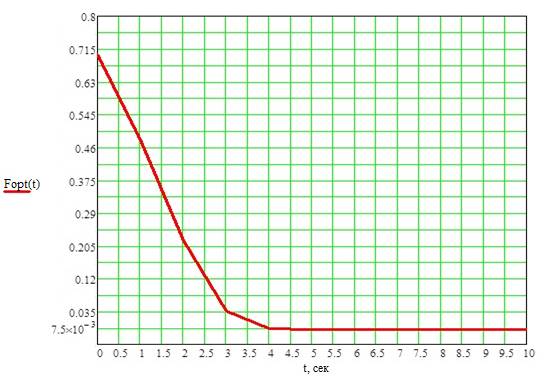
Рис 3 «Оптимального керування»

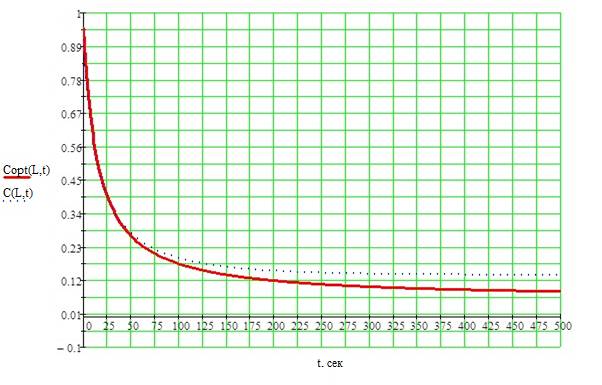
Рис 4 «Розв’язок математичної моделі в прямому часі при оптимальному керування»