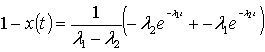ПРАКТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ ПЕРЕХОДНЫХ ПРОЦЕССОВ В СИСТЕМЕ ВТОРОГО ПОРЯДКА

Сухов Я.И., Гарькина И.А.

Пензенский государственный университет архитектуры и строительства

Рассмотрим гетерогенную систему, описываемую дифференциальным уравнением

. (1)

Пусть – корни характеристического уравнения

.

При

,

- корни характеристического полинома

При

.

Здесь - отклонение от равновесного состояния системы, определяемое стабилизированным параметром .

С учетом получим

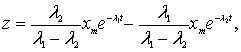
(2)

При описании переходных процессов естественным будет учет их поведения вблизи характерных точек; такими являются экстремальные точки, значения в экстремальных точках, интервалы выпуклости и вогнутости, точки перегиба. Имеем

Из = 0 следует

, ,.

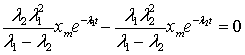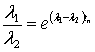Откуда абсцисса точки перегиба определится из условия

(3)

(при вогнутость сменяется на выпуклость).

Для определенности примем ; в (2) составляющая затухает быстрее, чем аналогичная составляющая, соответствующая корню . Если процесс определен экспериментально, то по концу этого процесса можно приближенное определить значение .

Примем (не ограничивается общностью рассуждений, так как это равносильно масштабированию ). Так как должны иметь

,

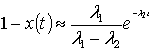то из

(4)

следует

,, ; ;

.

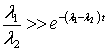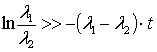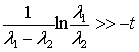Таким образом, при

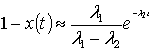
Введем

; .

Тогда

, , .

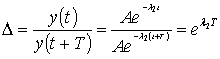Из следует

,,

.

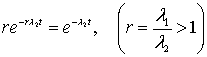Таким образом, абсцисса точки перегиба удовлетворяет трансцендентному уравнению (сложность аналитического решения)

.

(5)

Введем . Тогда

, , .

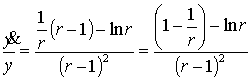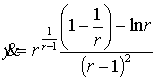Отсюда при . Справедливо

Так что в интервале не превышает e. Поэтому уравнение (5) имеет решение лишь при ; , а должно удовлетворять условию . При этом (тогда ). Из (3) следует 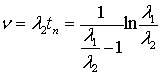, , а так как 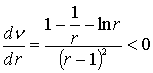, то с ростом уменьшается; .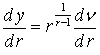

Указанная методика использовалась при разработке композиционных материалов по экспериментально определенным процессам формирования их свойств; подтвердилась ее эффективность.