ОПЫТ КОМПЛЕКСНОГО ПРОЕКТИРОВАНИЯ СИСТЕМЫ

УПРАВЛЕНИЯ ОБЪЕКТОМ НА ПОДВИЖНОМ ОСНОВАНИИ

Сухов Я.И., Данилов А.М.

Пензенский государственный университет архитектуры и строительства

Рассмотрим управление объектом на подвижном основании с использованием маломощной электромеханической системы управления. Для определенности уравнения движения в векторной форме принимаются в виде

;

(1)

где

, ;

- матрицы размерности соответственно;

.

Преобразуем систему (1) и приведем к виду

,

(2)

где

;

.

Матрица и столбец будут иметь блочную структуру

,

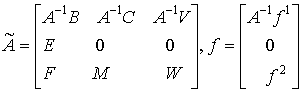где - единичная матрица.

С учетом высоких требований к вибрации конструктивных элементов от работы электропривода при синтезе целевая функция принимается в виде

,

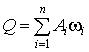где и - максимальные амплитуды и соответствующие им частоты в разложении в ряд Фурье ошибки системы:

;

- коэффициенты Фурье.

Синтез производился по приводимому ниже алгоритму.

1. По результатам эскизно-технического проекта выбираются структурная схема САУ и конструктивная схема (конструктивные подсистемы и параметры упругодемпфирующих связей между ними).

2. Составляются уравнения движения (математическая модель).

3. По предварительным конструктивным и динамическим проработкам

определяется область изменения параметров c .

4. По результатам линейного синтеза определяется исходная точка в пространстве параметров.

5. Методом Бокса-Уилсона определяются

,

и точка , в которой ,

где .

6. Если требуемая точность САУ не достигается, производится уточнение структурной схемы САУ при прежней конструктивной схеме и далее выполняются п.п. 2-5.

7. Если требуемая точность и тогда не достигается, то производится коррекция конструктивной схемы с использованием вибрационной карты конструкции, и выполняются п.п.2-6.

Итерационная процедура продолжается до достижения требуемой точности.

Значения определяются в результате интегрирования уравнений движения с параллельным разложением в ряд Фурье ошибки САУ в интервале ; промежуток времени , как и весь диапазон рассматриваемых частот, определяется из конструктивных соображений (для изучаемых систем с, ).

Сначала в пространстве параметров решалась задача

,

(3)

где - реальные части корней характеристического уравнения.

Точка в пространстве параметров, полученная в результате решения задачи (3), принималась в качестве исходной. Далее методом Бокса-Уилсона [1] производилась оптимизация параметров линейной системы по критерию

,

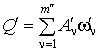где - отобранные резонансные частоты колебаний системы и соответствующие им амплитуды. Отбор требует большой осторожности при близких парциальных частотах (сложность сопоставления конструктивных подсистем с имеющимися на виброкарте частотами) и в связи с наличием нелинейностей в работе конструктивных элементов.

Точка, оптимальная в смысле минимума , принималась за исходную точку при нелинейном синтезе.

Эффективность предложенного подхода неоднократно подтвердилась при синтезе ряда систем управления объектами на подвижном основании.

Литература

1. Планирование эксперимента. Обработка опытных данных: монография / И.А.Гарькина [и др.]; под ред. проф. А.М.Данилова.– М.: Палеотип, 2005. – 272 с.