ПРИМЕР ВЫБОРА ВЕСОВЫХ КОНСТАНТ В ФУНКЦИОНАЛЕ

ДЛЯ ДИНАМИЧЕСКОЙ СИСТЕМЫ ПРИ ОЦЕНКЕ КАЧЕСТВА

Нугаев А.С., Данилов А.М.

Пензенский государственный университет архитектуры и строительства

Рассмотрим эргатическую систему, описываемую уравнениями движения

(, - вектор управления, - возмущающие воздействия).

Для оценки качества объекта управления в [1] предлагается использовать функционал качества вида

,

(1)

- корни характеристического полинома; - положительные весовые константы, - класс объекта в заданной N-балльной шкале.

Видом функционала учитывается зависимость стиля управления оператора от собственных частот колебаний и безразмерных коэффициентов демпфирования. В дальнейшем был разработан функционал, позволяющий производить объективную оценку объектов управления и для случая апериодичности. К сожалению, полученные оценки в значительной степени зависят от выбранных весовых констант. До сих пор они определялись на основе экспертных оценок операторов-экспертов. Очевидна возможность объективизации этих оценок с учетом коэффициентов корреляции между функционалом качества и вещественными и мнимыми частями корней характеристического полинома, входящими в функционал качества частных критериев.

Возможен и другой подход к выбору весовых констант. Проиллюстрируем его на примере объективизации оценок качества объекта с использованием десятибалльной шкалы Купера-Харпера.

Было установлено, что объекты с матрицами

,

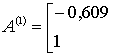
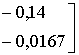
в уравнении движения принадлежат классу 3 (оценки по шкале Купера-Харпера - 2,5), а объект, которому соответствует матрица

,

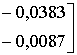принадлежит классу 4 (оценка по шкале Купера-Харпера - 3,5).

Для первой системы S₁ имеем:

, ; ,

(- след матрицы A; ).

В соответствии с (1)

.

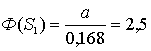Откуда

.

(2)

Для S₂: ; ; .

В соответствии с (1) и (2)

.

(3)

Для системы S₃: , ;.

.

(4)

Из (3) и (4) найдем ; .

На рис.1 приводятся области равных оценок для , , .

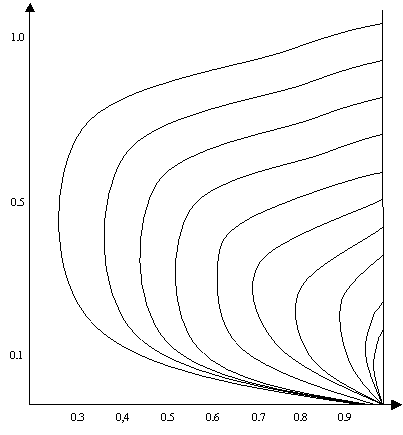
Рис.1. Границы областей равных оценок характеристик объекта

При выбранных весовых константах функционал использовался для объективизации экспериментальных оценок объектов. В частности, рассматривался объект, относящийся к четвертому классу и имеющий матрицу

.

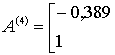
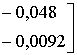Для системы S₄: . Легко показать, что .

Таким образом, класс системы S₄ равен 4 и предлагаемый функционал (1) с определенными выше весовыми константами позволяет объективизировать шкалу Купера-Хапера. Полученные области практически совпали с экспериментальными данными при оценке по шкале Купера-Харпера.

Литература

1. Гарькина И.А., Данилов А.М., Жесткова С.А. Объективизация шкалы Купера-Харпера / Новый университет. Серия: Технические науки. –2013. – № 1 (11). – С. 4-8.
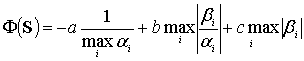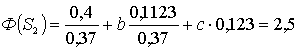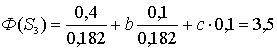