НЕКОТОРЫЕ ВОПРОСЫ АДЕКВАТНОСТИ

ДИФФЕРЕНЦИАЛЬНОГО И РАЗНОСТНОГО УРАВНЕНИЙ

ДЛЯ ОДНОГО КЛАССА ДИНАМИЧЕСКИХ СИСТЕМ

Петренко В.О., Гарькина И.А.

Пензенский государственный университет архитектуры и строительства

Рассмотрим вопросы адекватности дифференциального и разностного уравнений при применении метода регрессионной идентификации динамической системы. Представим простейший случай скалярного уравнения в виде разностного уравнения

.

Определим решение однородного разностного уравнения

.

Характеристическое уравнение имеет вид , тогда .

Общее решение однородного уравнения определится в виде

.

Методом вариации произвольной постоянной найдем решение неоднородного уравнения:

,

,

,

.

Таким образом, общее решение разностного уравнения будет иметь вид

.

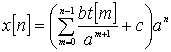Найдем решение при нулевом начальном условии , то есть

.

Откуда .

Так что решение рассматриваемого разностного уравнения имеет вид

или

.

Отметим, что соответствующее решение дифференциального уравнения имеет вид .

Для проверки надежности метода регрессионной идентификации по этой формуле определялся массив (- шаг дискретизации), который в методе наименьших квадратов (регрессионном методе) используется как исходный.

Считая, что элементы массива удовлетворяют разностному уравнению достаточно хорошо, составим функционал

.

Оценки a и b определяются как значения коэффициентов разностного уравнения, при которых функционал достигает минимума.

Должны иметь

,

.

Оценки коэффициентов определятся как решения системы уравнений:

, .

(1)

Введем:

, ,

, , .

Система (1) примет вид:

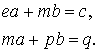
Откуда:

, .

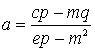Оценки (при различных ) приводятся в таблице:

0,05	1,045	0,056	0,995	1,11	0,5%	11%
0,1	1,101	0,113	1,001	1,13	0,1%	13%
0,2	1,220	0,236	1,020	1,18	2%	18%

Приведенные в таблице относительные погрешности и свидетельствуют о приемлемой точности параметрической идентификации. Однако полученные результаты еще не позволяют делать вывод о приемлемости регрессионного метода для идентификации. Поэтому необходимо определить восстанавливаемость коэффициентов уравнений по дискретным значениям их частного решения. Если уравнение движения с переменными коэффициентами, то их можно аппроксимировать аналитическими выражениями [1,2], например, с использованием полиномов Ньютона.

Литература

1. Планирование эксперимента. Обработка опытных данных: монография / И.А.Гарькина [и др.]; под ред. проф. А.М.Данилова. – М.: Палеотип. – 2005. – 272 с.

2. Данилов А.М., Гарькина И.А. Интерполяция, аппроксимация, оптимизация: анализ и синтез сложных систем: монография. – Пенза: ПГУАС. –2014. – 168 с.