Эксергетический анализ теплоты среды как возобновляемого источника энергии для тепловых насосов и холодильных машин

Д.т.н. Гришин А.П., д.т.н. Свентицкий И. И.

Показана возможность эксергетического анализа преобразований теплоты среды используемой тепловыми насосами (ТН) и холодильными машинами (ХМ) – наиболее эффективными генераторами теплоты и холода. Обоснована целесообразность использования применительно к ним таких показателей, как термодинамический и эксергетический КПД с такой же правомочностью, как и к тепловым силовым машинам.

ТН был изобретен в 1852 г выдающимся английским физиком Уильямом Томсоном (Кельвином) под названием «динамическое отопление». Практическое применение ТН было начато в 30 гг. ХХ столетия. Корректное объяснение принципа работы ТН и ХМ на основе второго начала термодинамики принципиально затруднено. В справочниках и иной технической литературе их работу объясняют «обратным циклом Карно», который от прямого цикла Карно отличается тем, что он осуществляется «не по часовой стрелке, а против неё». Такое объяснение не может отразить в должной мере высокую энергопреобразующую эффективность ТН и ХМ. В действительности в ТН и ХМ в качестве рабочего процесса использован самоорганизующийся энергоэкономный природный процесс – фазовый переход теплоносителя. Этот самоорганизующийся природный процесс используется в качестве рабочего процесса в тепловых насосах и холодильных машинах, где отдельные более быстрые молекулы, преодолевая поверхностное натяжение жидкости, самопроизвольно превращают ее в пар или газ. Унося часть энергии, отобранной от жидкости, они могут передать ее при конденсации в другом месте. Затрачивая работу на замкнутое перемещение жидкости и пара можно передавать теплоту от менее нагретого тела к более нагретому. Это дает принципиальное повышение (в разы по сравнению с традиционными тепловыми машинами) эффективности использования энергоносителя. Отечественные конструкции ТН на каждый кВт·ч потребляемой из сети электроэнергии продуцируют 2…2,5 кВт·ч теплоты для обогрева. Современные конструкции этих преобразователей зарубежных фирм имеют в два раза большую эффективность.

Для характеристики энергопреобразующей эффективности ТН и ХМ используют не показатель КПД, а соответственно: «нагревательный» и «холодильный» коэффициенты.

Широкое использование ТН началось в конце 60-х гг. ХХ столетия в связи с первым проявлением мирового энергетического кризиса. Согласно обзорной информации [1, с. 277] применение современных обратимых ТН для получения низкотемпературного тепла (отопление, кондиционирование, горячая вода) позволяет сократить расход топлива в 3 раза (для ТН типа воздух-воздух) и в 5 раза ( для ТН типа воздух-вода) по сравнению с применением традиционных топливных теплогенераторов. Правомочен вопрос: какое значение имеет теоретический коэффициент преобразования энергии тепловым насосом и как определить эксергию теплоты среды по ее преобразованию тепловым насосом?

Как известно, энтропийный метод в принципе не пригоден для анализа преобразований в ТН. В 80-е гг. ХХ столетия большинство энергетиков мира перешли от энтропийного анализа к эксергетическому, как к более простому и надежному, что благоприятствует его использованию для анализа преобразований в ТН. Как видно, из основных трудов проф. В.М. Бродянского – ведущего ученого по эксергетическому анализу – такой анализ для преобразований возобновляемых источников энергии еще не разработан [2, 3]. Очевидно, это, в известной мере, явилось причиной отставания РФ по использованию ТН. Это подтверждает опыт дискуссий по обсуждению необходимости применения ТН. В ответ на указание о высокой энергетической эффективности ТН оппоненты отмечают, что он «не имеет даже КПД». Отсутствие надежной методики для определения эксэргии теплоты среды не позволяло устанавливать значения термодинамического и эксергетического КПД для ТН и ХМ.

Исходной методической основой определения эксергиии теплоты среды логико-математическим методом представляется формула Карно, по которой устанавливают термодинамический КПД (η_Т) тепловой силовой машины:

. (1)

где Т₁ – температура теплоносителя на входе в машину; Т₀ – то же самое на выходе из машины. Этот показатель общепризнан, его широко применяют.

Отметим, что в соответствии с этой методикой эксергию, потенциальную работоспособность первичного энергоносителя, используемого для получения теплоты в тепловых силовых машин (е_Т) определяется умножением его общего энергосодержания (Е) на термодинамический КПД.

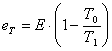=Е ƞ_{Т ,} (2)

Распространяя второе начало термодинамики на необратимые процессы еще Р. Ю. Клаузиус отмечал, что при анализе простого кругового процесса тепловой машины надо учитывать происходящие в ней одновременно два процесса: превращение некоторого количествам теплоты в работу (или наоборот) и одновременный переход тепла от более нагретого тела к менее нагретому телу (или наоборот). Он считал, что между этими двумя процессами существует определенная связь, которая не зависит от природы тела (теплоносителя), совершающего круговой процесс. При этом он правильно отмечал, что « второе начало должно выражать отношение между этими двумя превращениями». Далее он доказывал, что оба превращения «следует рассматривать как явления одинаковой природы; таких два превращения, которые могут замещать друг друга, он называет эквивалентными превращениями. При этом необходимо иметь в виду, что оба превращения протекают в противоположных направлениях» [цит. по 4, т. 1, с. 212].

В этом представлении Клаузиуса содержится в зачаточном виде ценная мысль для решения нашей задачи – обоснование эксергетического подхода для оценки преобразования теплоты среды и обоснования правомочности использования показателей термодинамического и эксергетического КПД для ТН и ХМ. Под « двумя превращениями» Клаузиус понимал, очевидно, следующих два процесса: процесс преобразования теплоты в работу, протекающий в тепловой силовой машине – прямой процесс - и процесс преобразования работы в теплоту, происходящий в ТН и ХМ – обратный процесс. Этих два взаимно противоположных процесса можно рассматривать как прямой и обратный.

Прямой процесс общепринято характеризуют величиной термодинамический КПД тепловой силовой машины (η_Т), следовательно, обратный процесс – процесс преобразования работы посредством ТН и ХМ в теплоту, в соответствии с определением обратной величины в математической логике [6] , можно характеризовать обратной величиной термодинамическому КПД – 1/(η_Т). Исходя из этого, термодинамический КПД теплового насоса и холодильной машины (η_тн,хм) будет определяться с учетом (1) зависимостью:

η_тн,хм = 1/ η_Т = Т₁/ Т₁ - Т₀, (3)

Зависимость (3) совпадает с зависимостью для определения «нагревательного» и «холодильного» коэффициентов применяемых для ТН и ХМ, что подтверждает правильность обоснования (3)

Для дальнейшей проверки правильности выражения (3) обратимся к характеристикам современных тепловых насосов. приведенных в Интернет [7]. У всех ТН фирмы Vitocal , фрагмент характеристик которых приведен в табл.1, минимальная температура на входе составляет +5 ^оС, а максимальная температура на выходе равна +55 ^оС [7]. Подставив в формулу (3) эти значения температур и произведя вычисления, получим значения термодинамического КПД тепловых насосов Vitocal равное 6,5; которое несколько выше значений КПД, приведенных в табл. 1 (5,6). Значения КПД, приведенные фирмой, очевидно, являются измеренными номинальными значениями реального КПД теплового насоса, так как эти значения совпадают с отношениями потребляемой электрической мощности и производимой тепловой мощностью. Исходя из вышеприведенного, эти значения не являются термодинамическими КПД тепловых насосов. Их, очевидно, целесообразно приводить в технической документации, наряду с номинальными измеренными значениями КПД, как это сделано фирмой Vitocal.

Таблица 1. Фрагмент характеристик теплового насоса типа Vitocal [7].

Показатель	Тип теплового насоса
	WW240	WW254	WW268	WW280
Номинальная тепловая мощность, кВт (рабочая точка W10/W35 в соответствии с EN255)	52,0	73,2	90,2	106,8
Хладопроизводительность, кВт	42,8	60,0	74,0	87,8
Потребляемая электрическая мощность, кВт	9,2	13,2	16,2	19,0
Коэффициент полезного действия	5,6	5,6	5,6	5,6

По значениям реального КПД ТН в номинальном режиме и его термодинамического КПД можно определить значение эксергетического КПД теплового насоса. Он будет равен: 5,6/6,5 = 0,8. Значение эксергетического КПД любого преобразователя энергии характеризует меру совершенства данной конструкции определенного его вида.

Исходя из значения эксергетического КПД обратимого теплового насоса фирмы Vitocal (0,8), можно считать, что эта конкретная конструкция является достаточно совершенной для обратимых тепловых насосов типа воздух – вода. Отметим, что без определения термодинамического КПД любого преобразователя энергии невозможно установить его эксэргетический КПД. Второй независимый метод определения термодинамического КПД ТН и ХМ возможен на основе определения значений теплоты фазовых переходов энергоносителя, которые являются основными рабочими процессами в этих преобразователях энергии.

Характерная особенность основных законов энергетики – трех начал термодинамики – в том, что их определения носят запретительный характер. Наиболее ярко эта особенность отражена во всех существующих определениях второго начала. Его исходное определение: невозможно передать теплоту от холодного тела к более теплому телу. Приняв во внимание работу холодильной машины, и изобретя «динамическое отопление», лорд Томпсон (Кельвин) уточнил исходное определение второго начала, дополнив его словом «самопроизвольно». Однако это уточнение не устранило неполноценность второго начала как самостоятельного закона природы. Это видно, например, из общего определения КПД ТН, приведенного в БСЭ, в котором отмечается, что этот показатель может быть больше единицы, так как этот преобразователь использует не только электрическую энергию, но и теплоту окружающей среды. Реальный КПД ТН (η_ТН) эмпирически определяют по выражению:

(4)

где Q_вых – теплота, закачиваемая ТН в обогреваемое помещение; W_э – электроэнергия, потребляемая ТН; Q_ТС – теплота среды, используемая им.

Однако теплоту Q_ТС теоретически можно определить только по формуле Карно (1), но так как теплота среды не имеет температурного градиента, то теоретическое значение Q_ТС равно нулю. Энтропия теплоты среды максимальна, следовательно, ее потенциальная превратимость (работоспособность, эксэргия) равна нулю. Этот вывод на основе второго начала термодинамики не согласуется с практическими результатами по высокой энергопреобразующей эффективности ТН. Его показатель эффективности преобразования электроэнергии в низкотемпературную теплоту для нагрева, называемый чаще всего нагревательным коэффициентом, достигает 560 % в современных конструкциях обратимых тепловых насосов типа воздух-вода [7]. Значения КПД ТН и ХМ больше единицы, что, казалось бы, противоречит общему определению КПД, но это противоречие имеет современное естественнонаучное объяснение. Первоначальное классическое определение КПД относилось к преобразованию одного и того же вида энергии – механической работы. В термодинамике этот показатель стали использовать для характеристики преобразования теплоты в работу, тем самым было сделано принципиальное отступление от классического его понимания. Вторая особенность этого объяснения состоит в ограниченности приложения второго начала термодинамики только к равновесным, не самоорганизующимся явлениям [8]. В ТН и ХМ в качестве рабочего процесса использован самоорганизующийся фазовый переход испарение – конденсация. По природе своей этот самоорганизующийся процесс энергоэкономен и поэтому не согласуется со вторым началом термодинамики.

Вопросу использования показателя КПД применительно к ТН и ХМ, а также превышению его значения единицы, большое внимание уделено В.М. Бродянским с соавторами в книге «Эксэргетический метод и его приложение». Они отмечают [3, с. 137]: «Несравненно более глубокое понимание трудностей общего научного определения КПД проявил акад. А.А. Харкевич. Он писал: «Методические трудности здесь носят фундаментальный характер... Главная из них ... состоит в определении того, что именно следует рассматривать в качестве полезного действия данного устройства, и подыскании количественной меры этого полезного действия». Рассматриваемую трудность этот автор считает «просто непреодолимой «при теперешнем понимании сути дела».

Под «теперешним пониманием» А.А. Харкевич как раз и имел в виду [3, с. 137]: «… использование в качестве … значений энергии разных видов, выбранных из энергетического баланса, т.е. в конечном счете, несоответствие понятия коэффициента полезной эффективности (КПЭ) требованиям к КПД». Это привело его к пессимистическому мнению, что «элегантная простота первоначального определения КПД утрачена в области теплотехники невозвратимо». Действительно, первоначальное определение КПД (effeсt utile), введенное в науку (конец XVIII – начале XIX вв.) французскими учеными Карно, Навье, Понселе и развитое Кориолисом, было элегантно простым: КПД определялся отношением полученной работы к затраченной. Поскольку объектом оценки были механические и гидравлические машины, такое определение было вполне строгим и отвечало всем требованиям, т.е. КПД был всегда меньше единицы, разность числителя и знаменателя точно равнялась потере. Соответственно определение КПД было и строго однозначным – никаких других величин из отношения двух работ получить нельзя. Объясняется все это тем, что сопоставляемые величины энергии были качественно однородны – работа на входе и работа на выходе. Однако, как только этот подход был перенесен «в область теплотехники» – на тепловые машины, где сопоставлялись качественно различные виды энергии в переходе – теплота и работа, «элегантная простота» действительно была утрачена, ибо единый КПД превратился в разные коэффициенты преобразования, не отвечающие требованиям к классическому определению КПД.

Заключение. Обоснование эксергетического анализа преобразований теплоты среды - наиболее доступного возобновляемого источника энергии - и выявление целесообразности использования показателей термодинамического и эксергетического КПД применительно к ТН и ХМ с такой же надежностью, как к тепловым силовым машинам, устраняет сомнения в высокой энергетической эффективности этих преобразователей энергии. Необходима неотложная модернизация: замена морально и физически устаревших топливных теплогенераторов на мини-ТЭС с когенерацией тепловой энергии и использованием ТН.

Литература

1. Федоренко В.Ф. (под ред.), Инновационное развитие альтернативной энергетики: науч. изд. ч.2, -М.; ФГНУ «Росинформагротех», 2011.

2. Бродянский В.М., Фратшер В., Михалек К. Эксергетический метод и его приложения. М.: Энергоатомиздат, 1988.

3. Бродянский В.М. Эксергетический метод термодинамического анализа. М.: Энергия, 1973.

4. Гельфер Я.М. История и методология термодинамики и статистической физики. Т.I. М.: Высшая школа, 1969.

5. Бочаров В.А., Маркин В. И. Основы логики: Учебник. М.: ИНФРА-М, 2001.

6. Интернет: http://www.viessmann.ru.

7. Свентицкий И.И. Энергосбережение в АПК и энергетическая экстремальность самоорганизации. М., ГНУ ВИЭСХ, 2007.