К.ф.-м. н. Габасова
О.Р.
Белорусский национальный технический университет
Оптимизация линейной гибридной
системы в классе дискретных управляющих воздействий
1. В классе дискретных управляющих
воздействий (![]() ) рассмотрим задачу оптимизации линейной гибридной системы
[1]
) рассмотрим задачу оптимизации линейной гибридной системы
[1]
![]() , (1)
, (1)
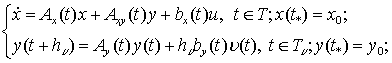 (2)
(2)
![]() . (3)
. (3)
Здесь ![]() – состояние непрерывной части системы в момент времени
– состояние непрерывной части системы в момент времени ![]() ,
, ![]() – состояние дискретной части системы;
– состояние дискретной части системы; ![]() – состояние гибридной системы,
– состояние гибридной системы, ![]() – значения
управляющих воздействий в момент
– значения
управляющих воздействий в момент ![]() .
.
Под траекторией
системы (2), соответствующей управляющим воздействиям ![]() , будем понимать единственную пару из непрерывной функции
, будем понимать единственную пару из непрерывной функции ![]() , и дискретной с периодом квантования
, и дискретной с периодом квантования ![]() в прямом времени
функции
в прямом времени
функции ![]() , которые удовлетворяют уравнениям (2).
, которые удовлетворяют уравнениям (2).
Управляющие воздействия ![]() назовем программой гибридной
системы, если на соответствующей им траектории
назовем программой гибридной
системы, если на соответствующей им траектории ![]() системы (2) выполняются
ограничения (3). Программа
системы (2) выполняются
ограничения (3). Программа ![]() называется оптимальной,
если на ней критерий качества (1) достигает максимального значения:
называется оптимальной,
если на ней критерий качества (1) достигает максимального значения: ![]() , где максимум вычисляется по всем программам. Суботпимальную (
, где максимум вычисляется по всем программам. Суботпимальную (![]() -оптимальную) программу
-оптимальную) программу ![]() определим неравенством
определим неравенством ![]()
2. В [1] доказано, что состояние гибридной
системы (2) в момент ![]() вычисляется по
формуле Коши
вычисляется по
формуле Коши
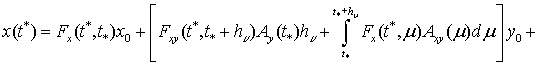
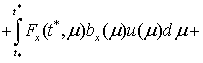
![]() (4)
(4)
![]()
![]() ,
,
где функция ![]()
![]() , дифференцируема по
, дифференцируема по ![]() , функции
, функции ![]()
![]() , дискретны в обратном времени с периодом квантования
, дискретны в обратном времени с периодом квантования ![]() − компоненты фундаментальной матрицы решений гибридной
системы (2), удовлетворяющие уравнениям
− компоненты фундаментальной матрицы решений гибридной
системы (2), удовлетворяющие уравнениям
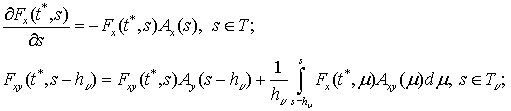 (5)
(5)
![]()
![]() (6)
(6)
Подставив выражения (4) в (1) – (3), получим задачу
линейного программирования, эквивалентную исходной задаче
![]() ,
,
![]() ,
, ![]() , (7)
, (7)
где ![]() ;
;![]() ;
;![]() ,
, ![]() выражаются через
выражаются через ![]() и исходные параметры
задачи.
и исходные параметры
задачи.
3. Пусть ![]()
![]() ;
; ![]() ,
, ![]() ,
, ![]() , −
произвольные множества;
, −
произвольные множества; ![]() ;
; ![]()
![]() .
.
Определение 1.
Множество ![]() называется опорой задачи (1) – (3), если не вырождена
матрица
называется опорой задачи (1) – (3), если не вырождена
матрица ![]() , т.е.
, т.е. ![]() .
.
Следуя [2], подсчитаем вектор потенциалов ![]() :
: ![]() , где
, где ![]()
Определение 2. Совокупность ![]() с компонентами
с компонентами
![]() , называется копрограммой
задачи (1) – (3), сопровождающей
опору
, называется копрограммой
задачи (1) – (3), сопровождающей
опору ![]() .
.
Можно показать [1], что 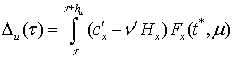
![]() ;
;
![]()
![]()
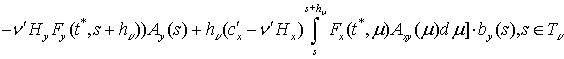 .
.
Введём функции ![]()
![]() ,
, ![]()
![]() ,
,![]() . (8)
. (8)
Из (5), (6) получаем соотношения
![]()
![]()
![]()
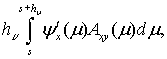
![]() ; (9)
; (9)
Следовательно, функции (8) являются решением сопряженной системы (9)
с начальными условиями
![]() ,
,![]() (10)
(10)
Определение 3. Котраекторией, сопровождающей опору ![]() , назовём пару (
, назовём пару (![]() ), состоящую из непрерывной функции
), состоящую из непрерывной функции ![]() и дискретной в обратном
времени с периодом квантования
и дискретной в обратном
времени с периодом квантования ![]() функции
функции ![]() , которые удовлетворяют сопряженной системе (9) с начальными
условиями (10).
, которые удовлетворяют сопряженной системе (9) с начальными
условиями (10).
Следовательно,
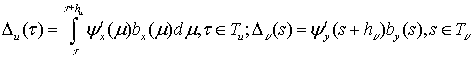 .
.
Принцип
ε-максимума. При любом ε
≥ 0 для ε-оптимальности программы ![]() необходимо и
достаточно существование такой опоры
необходимо и
достаточно существование такой опоры ![]() , при которой на сопровождающей ее котраектории
, при которой на сопровождающей ее котраектории ![]() выполняются условия квазимаксимума:
выполняются условия квазимаксимума:
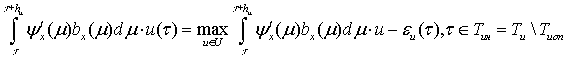 ;
;
![]() ; (11)
; (11)
![]() .
.
Доказательство основано на формуле приращения критерия
качества и проводится аналогично
доказательству соответствующего результата для задачи линейного
программирования [2]. При ![]() из (11) следует
из (11) следует
Принцип
максимума. Для оптимальности
программы ![]() необходимо и
достаточно существование такой опоры
необходимо и
достаточно существование такой опоры ![]() , при которой на сопровождающей ее котраектории
, при которой на сопровождающей ее котраектории ![]() выполняются условия максимума:
выполняются условия максимума:
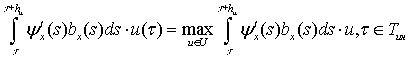 ;
;
![]() .
.
Литература
1.
Габасова О.Р. Оптимизация линейных гибридных систем
управления / О.Р. Габасова // Вестник БНТУ. – 2007. – № 2. – С. 71 – 75.
2.
Габасов Р., Кириллова
Ф.М., Тятюшкин А.И. Конструктивные методы оптимизации. Ч.1. Линейные задачи.
Мн.: Университетское, 1983. 214 с.