Шилинец В. А., Пташинская О. И.

Белорусский государственный педагогический университет

О РЕШЕНИИ ОДНОЙ ЛИНЕЙНОЙ ДИФФЕРЕНЦИАЛЬНОЙ СИСТЕМЫ В ЧАСТНЫХ ПРОИЗВОДНЫХ МЕТОДАМИ F - МОНОГЕННЫХ ФУНКЦИЙ

Известен ряд работ [1-7], в которых для исследования уравнений в частных производных применялись гиперкомплексные F-моногенные функции [8]. В настоящей работе исследуется с помощью F-моногенных функций система трёх дифференциальных уравнений в частных производных с тремя неизвестными функциями. Для исследования данной системы используются гиперкомплексные функции

. (1)

Следует подчеркнуть, что функции вида (1) применяются для исследования функционально-инвариантных решений системы дифференциальных уравнений Максвелла [9, 10] для электромагнитного поля в пустоте.

Множество всех комплексных или действительных функций, однозначно определённых в некоторой односвязной области евклидова пространства , где , и непрерывно дифференцируемых раз в области , будем обозначать (случай соответствует функциям, непрерывным в области ).

Множество всех функций вида

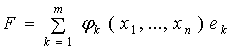
(; – базис некоторой линейной ассоциативно-коммутативной алгебры с единицей над полем комплексных или действительных чисел) будем обозначать .

Пусть даны функции , . Формальные производные – функции от , которые определяются из системы

,

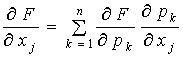где 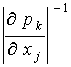существует; [11, 12].

Пусть функции , . Тогда функция будет моногенной в смысле В. С. Фёдорова (F-моногенной) в области по функциям [13], если найдутся такие единственные функции , что для всех точек области

.

Рассмотрим систему дифференциальных уравнений в частных производных вида

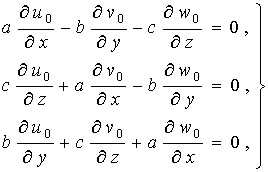(2)

где – искомые комплекснозначные функции трёх действительных переменных ; – некоторые действительные или комплексные константы. Все рассматриваемые функции предполагаются непрерывно дифференцируемыми (но не обязательно аналитическими) в некоторой области евклидова пространства .

Пусть алгебра – ассоциативно-коммутативная алгебра с базисом , где закон умножения определяется равенством . Введём в рассмотрение гиперкомплексную функцию

.

Базой будем называть совокупность функций, по которым находятся формальные производные [12]. В качестве базы формальных производных выбираем гиперкомплексные функции

, , ,

где – некоторые действительные или комплексные константы, отличные от нуля. Отметим далее, что имея заданные действительные или комплексные константы , всегда можно подобрать такие константы , для которых выполняются равенства

, , .

Константу выбираем произвольно (но не равную нулю).

Легко показать, что система дифференциальных уравнений в частных производных (2) эквивалентна уравнению в формальных производных

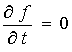, (3)

где

, .

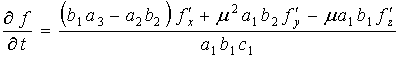Равенство (3) свидетельствует о том, что – произвольная моногенная в смысле В. С. Фёдорова относительно функций и в области функция. В этом случае условимся писать .

Исследовав структуры функций класса , была получена следующая теорема.

Теорема. Общее решение системы дифференциальных уравнений в частных производных (2) имеет вид:

,

,

,

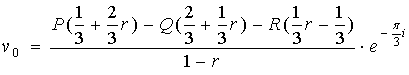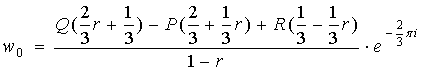где , , , , , ;

(, ) – произвольная комплексная функция, F-моногенная по функциям и ( и , и ) в области ; .

Литература

1. Стельмашук Н. Т. О некоторых линейных дифференциальных системах в частных производных // Сибирский математический журнал, 1964. – Т. 5, № 1. – С. 166-173.

2. Фёдоров В. С., Стельмашук Н. Т. Решение некоторых уравнений в частных производных методами F - моногенных функций // Rev. Roum. de Math. Pures et Appl., 1973. – Т. 18, № 2. – Р. 233-241.

3. Кусковский Л. Н. О краевой задаче типа Римана - Гильберта // Дифференциальные уравнения, 1975. – Т. 11, № 3. – С. 523-532.

4. Стельмашук Н. Т., Пенчанский С. Б. О решении одной линейной дифференциальной системы в частных производных методами

F-моногенных функций // Дифференциальные уравнения, 1990. – Т. 26, № 4. – С. 724-727.

5. Стельмашук Н. Т., Шилинец В. А. Метод формальных производных для решения задачи Коши для одной системы дифференциальных уравнений в частных производных // Дифференциальные уравнения, 1993. – Т. 29, № 11. – С. 2019-2020.

6. Stelmashuk N. T., Shylinets V. A. The solution of the boundary value problem for a system of equations in formal derivatives by means dual differential operators // Труды института математики НАН Беларуси, 2004. – Т. 12, № 2. – С. 170-171.

7. Стельмашук Н. Т., Шилинец В. А. О преобразовании к каноническому виду системы линейных уравнений в частных производных с помощью двойных дифференциальных операторов // Весці НАН Беларусі. Сер. фіз.-мат. навук, 2008. – № 2. – С. 61-65.

8. Фёдоров В. С. Основные свойства обобщённых моногенных функций // Известия вузов. Математика, 1958. – № 6. – С. 257-265.

9. Стельмашук Н. Т. Об одном исследовании системы Максвелла с помощью F-моногенных функций // Журнал вычислительной математики и математической физики, 1967. – Т. 7, № 2. – С. 431-436.

10. Стэльмашук М. Т., Шылінец У. А. Пабудова інтэгральных выяўленняў для функцыянальна -інварыянтных рашэнняў сістэмы дыферэнцыяльных раўнанняў Максвэла // Весці БДПУ, 1999. – № 2. – С. 147-150.

11. Гусев В. А. Об одном обобщении ареолярных производных // Bul. stiint. al Instit. politehnic Timisoara, 1962. – Т. 7, f. 2. – P. 223-238.

12. Стельмашук Н. Т. Определение и свойства формальных производных // Математика: сб. науч. тр. – Мн.: МГПИ, 1973. – С. 52-59.

13. Морев И. А. Об одном обобщении понятия моногенных функций // Математический сборник, 1957. – Т. 42, № 2. – С. 197-206.