Карачун В.В., Мельник В.Н.

Национальный технический университет Украины «КПИ»

СИСТЕМАТИЧЕСКАЯ ПОГРЕШНОСТЬ ПОПЛАВКОВОГО ПРИБОРА В РЕВЕБРАЦИОННОМ ПРОСТРАНСТВЕ

Запишем уравнение двухстепенного гироскопа в виде:

где момент инерции подвижной части; соответственно коэффициенты демпфирования и жескости пружины; угол поворота поплавка; другие моменты, действующие на выходной оси.

Решая уравнение можно вычислить угол . В случае интегрирующего гироскопа достаточно положить равной нулю жесткость пружины, то есть принять .

Установившееся значение угла поворота , соответствующее «ложной» угловой скорости и обусловленное влиянием прошедшего внутрь прибора акустического излучения, будет определяться формулами –

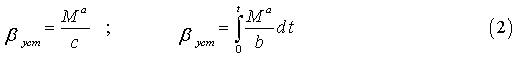
соответственно для датчика угловой скорости и интегрирующего гироскопа.

Если координаты точки приложения равнодействующей известны, надо воспользоваться формулой:

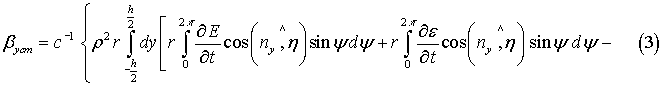
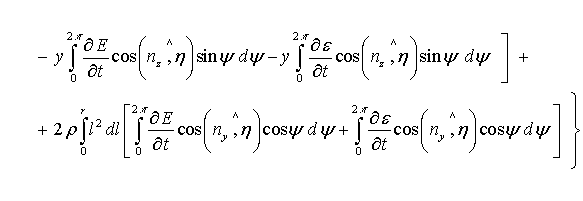
для дифференцирующего гироскопа и формулой

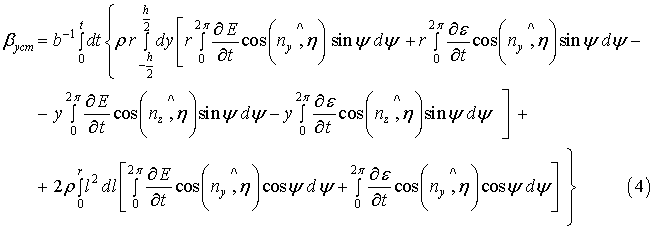
для интегрирующего гироскопа.

Потенциал подчиняется трехмерному волновому уравнению Лапласа

и начальным условиям

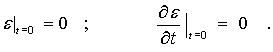
При функция и на поверхности поплавка имеет место условие

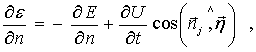
где - скорость точки поверхности поплавка.

Пусть на поплавок действует плоская монохроматическая волна давления, например, вида

а потенциал скорости падающей и дифракционной волн определяются соотношениями

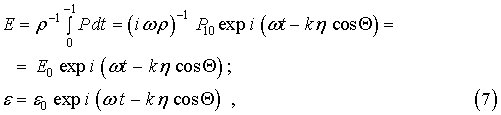
где угол есть угол преломления, определяемый из закона Снеллиуса, и состоит в равенстве фазовых скоростей распространения волн вдоль границы сред ( в данном случае взвешивающая жидкость и поплавок; давление в падающей волне.

Тогда установившееся значение акустической погрешности, например, датчика угловых скоростей будет определяться формулой

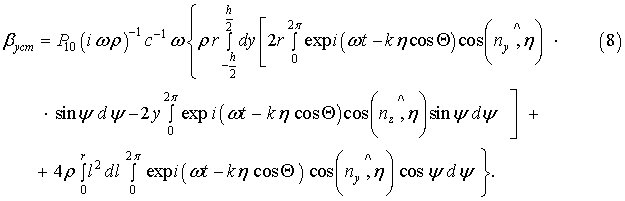
Решение уравнения (1) дает возможность установить закономерности изменения этой погрешности во времени.