К. ф.-м. н. Мирская Е.И., Марчук А.Ю.

Брестский государственный университет имени А.С. Пушкина,

Республика Беларусь

Исследование скорости сходимости первого момента сглаженной оценки взаимной спектральной плотности

Спектральный анализ временных рядов является одним из основных направлений в исследованиях ученых многих стран мира, причем особое внимание уделяется методам спектрального анализа стационарных случайных процессов. В анализе временных рядов одной из главных проблем является построение оценок спектральных плотностей и исследование их статистических свойств.

Рассмотрим действительный стационарный случайный процесс , с , неизвестной взаимной спектральной плотностью

Пусть – последовательных наблюдений, полученных через равные промежутки, за составляющей процесса .

Предполагаем, что число наблюдений представимо в виде , где – число пересекающихся интервалов, содержащих по наблюдений, а принимает целочисленные значения, .

Используя методику Бриллинджера Д. [1], в качестве оценки взаимной спектральной плотности исследована статистика вида

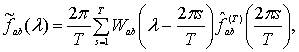(1)

где – спектральное окно, а , – оценка взаимной спектральной плотности процесса , построенная по методу Уэлча

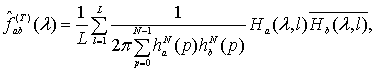(2)

где задано выражением

(3)

, причем наблюдения сглаживаются одним и тем же окном просмотра данных

В данной работе исследована скорость сходимости математического ожидания оценки , предполагая, что , , удовлетворяет условию

, (4)

для любых , – некоторая положительная постоянная,

Предположение 1. Пусть окна просмотра данных ограничены единицей и имеют ограниченную постоянной вариацию.

Предположение 2. Пусть непрерывная, периодическая функция с периодом , имеет ограниченную вариацию и является ядром.

Лемма 1. Для ядра , , при любом

(5)

Доказательство. Запишем

где

Так как функция непрерывна на , следовательно, для любого существует что как только то , поэтому

можно сделать сколь угодно малым за счет выбора . Значит,

Рассмотрим .

Учитывая предположение 2,

Лемма доказана.

Теорема 1. Если взаимная спектральная плотность непрерывна в точке и ограничена на , окна просмотра данных удовлетворяют предположению 1, а спектральные окна предположению 2, то для оценки , заданной выражением (1), справедливо соотношение

(6)

Доказательство. Используя свойства математического ожидания и функции вида

(7)

где

запишем

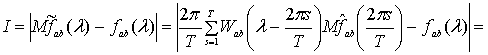
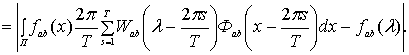
Откуда, учитывая лемму Д5.1 работы [1], получим

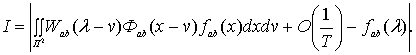
Сделаем замену переменных тогда,

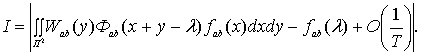
Сделаем замену переменных , получим

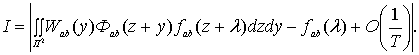
Учитывая, что свертка двух ядер является ядром,

-

ядро. Тогда,

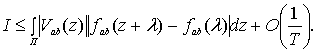
Так как взаимная спектральная плотность непрерывна в точке и ограничена на , а является ядром, получим требуемый результат. Теорема доказана.

Теорема 2. Если взаимная спектральная плотность , , , удовлетворяет соотношению (4), то для математического ожидания оценки , , задаваемой (1), имеет место равенство

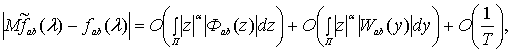
где а задается выражением (7).

Доказательство. Учитывая, что математическое ожидание оценки имеет вид

,

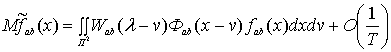используя соотношения (4) и (5), получим требуемый результат. Теорема доказана.

Литература:

1. Бриллинджер, Д. Временные ряды. Обработка данных и теория. - М.:Мир, 1980. - 536 с.