К. ф.-м. н. Марзан С.А.
Брестский государственный университет
имени А.С. Пушкина,
Республика Беларусь
Приближенное решение задачи Коши для системы
нелинейных дифференциальных уравнений
с дробными производными Капуто
Обозначим через ![]() модифицированную
дробную производную, определяемую формулой
модифицированную
дробную производную, определяемую формулой
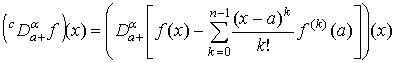 , (1)
, (1)
где ![]() – дробная производная
Римана-Лиувилля [1] функции
– дробная производная
Римана-Лиувилля [1] функции ![]() , заданной на [a;b], комплексного порядка
, заданной на [a;b], комплексного порядка ![]() (
(![]() ), Re(
), Re(![]() )>0, n=[Re(
)>0, n=[Re(![]() )]+1 при
)]+1 при ![]() ={1,2,…}, и
={1,2,…}, и ![]() при
при ![]() . Если
. Если ![]() ,
, ![]() (
(![]() ) и y(x)ÎCn[a;b] –
функция, n раз непрерывно дифференцируемая на [a;b], то при
) и y(x)ÎCn[a;b] –
функция, n раз непрерывно дифференцируемая на [a;b], то при ![]() производная
производная ![]() совпадает с обычной
производной, а при
совпадает с обычной
производной, а при ![]() оператор
оператор ![]() представляется в виде композиции оператора
дробного интегрирования
представляется в виде композиции оператора
дробного интегрирования ![]() [1] и оператора
дифференцирования
[1] и оператора
дифференцирования ![]() :
:
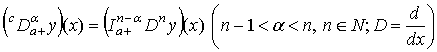 . (2)
. (2)
Конструкция
(2) была введена итальянским механиком Капуто [2], и поэтому выражения (1) и
(2) называют дробными производными Капуто порядка ![]() .
.
Работа посвящена применению
модифицированного апрроксимационно-итеративного метода [3] для приближенного
решения задачи Коши для системы нелинейных дифференциальных уравнений с дробными
производными Капуто порядков ![]() ,
, ![]() (k=1,2,…,p,
(k=1,2,…,p, ![]() )
)
![]() , (3)
, (3)
с начальными условиями
![]() ,
, ![]()
![]() , (4)
, (4)
посредством
приближенного решения равносильной ей [4] системы интегральных уравнений
Вольтерра
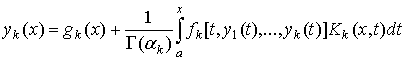 ,
,
где 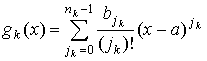 ,
, ![]()
![]() .
.
Далее
будем использовать стандартные интерполяционные многочлены Лагранжа ![]() , построенные по узлам
, построенные по узлам
![]() ,
, ![]()
![]() . (5)
. (5)
Будем
считать, что ![]() при
при ![]() , и определим операторы
(интерполяционные многочлены)
, и определим операторы
(интерполяционные многочлены) ![]() формулой
формулой
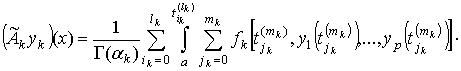
![]() .
.
Здесь
узлы ![]() и
и ![]() определяются по формуле (5), а
определяются по формуле (5), а ![]() и
и ![]() – фундаментальные многочлены Лагранжа по узлам
– фундаментальные многочлены Лагранжа по узлам ![]() и
и ![]() соответственно (k=1,2,…,p).
соответственно (k=1,2,…,p).
Построим
при помощи итерационного процесса по v функции
![]() вида
вида
![]() ,
, ![]() , k=1,2,…,p;
, k=1,2,…,p; ![]()
Теорема 1. Функции ![]() являются алгебраическими многочленами вида
являются алгебраическими многочленами вида
![]() ,
, ![]()
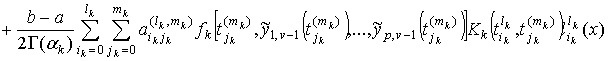 ,
,
где для ![]() ,
, ![]()
![]() , k=1,2,…,p
, k=1,2,…,p
![]()
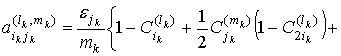
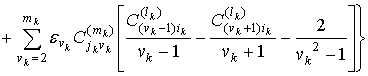 ,
,
![]() ,
, ![]() при
при ![]() и
и 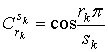 .
.
Доказана
теорема существования приближенного решения задачи Коши (3)-(4), получена
оценка точного и приближенного решения.
Список литературы
1. Самко
С.Г., Килбас А.А., Маричев О.И. Интегралы и производные дробного порядка и
некоторые их приложения. – Минск: Наука и техника, 1987. – 687 с.
2. Caputo M. Linear model of dissipation whose
Q is almost frequency independent // Geophis.
J. Astronom. Soc. – 1967. –Vol. 13. – P. 529-539.
3. Дзядык
В.К. Аппроксимационные методы решения дифференциальных и интегральных уравнений.
– К.: Наук. думка, 1988. – 302 с.
4.
Марзан С.А. Нелинейное дифференциальное уравнение дробного порядка с дробной
производной Капуто в пространстве непрерывных функций // Труды Ин-та мат-ки,
Минск. – 2004. – Т.12, №2. – С. 99-103.