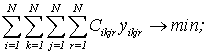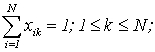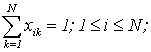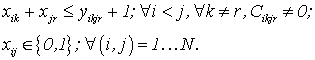Математика/ 5. Математичне моделювання

Скрильник І.І.

ТЕОРІЯ ПАТТЕРНІВ ТА ПЕРСПЕКТИВИ ЇЇ ЗАСТОСУВАННЯ І РОЗВИТКУ

Полтавський національний технічний університет, Україна

Сьогодення вимагає від розробників стандартизувати розв’язання багатьох класів практичних задач. Це означає, що потрібно створити таку “базу розв’язків” задач того чи іншого класу, за допомогою якої можна знаходити готові шаблони рішень - паттерни.

Основоположником теорії паттернів є американський учений Ульф Гренадер. Він намагався побудувати теорію логічних шаблонів для моделювання образів, що мають внутрішні структури і чіткі зовнішні границі. Суть теорії паттернів полягає у тому, що основними елементами є об’єкти під назвою “утворюючі” (англ. generators). Вони формально описуються символьними математичними співвідношеннями і відображаються на папері наочними схемами. Утворюючі слугують математичними і наочними моделями фізичних та логічних об’єктів реального світу. В утворюючій є невід’ємні від неї зв’язки (англ. bonds). Попарно з’єднуючи зв’язки, з об’єктів конструюють конфігурації теорії паттернів, які слугують моделями реальних фізичних та логічних систем, що складаються із взаємозв’язаних об’єктів. Ця теорія має велику гнучкість, оригінальність, глибину математичних та філософських ідей, її використовують у різних областях знань.

У практичному розумінні прийнято вважати, що паттерн – це документ, шаблон або структура, яка описує загальний розв’язок деякої проблеми. У цьому випадку розробники використовують розв’язок задачі на основі паттерна з метою стандартизації та скорочення часу на розробку проекту. Це значить, що маючи певний шаблон розв’язку задач, які належить до якогось класу, не потрібно кожну задачу із цього класу розв’язувати заново.

Такий підхід має велике практичне значення при розв’язанні прикладних задач у різних сферах діяльності людини. Теорію паттернів можна застосувати до розв’язання класів економічних задач, логістики, розподілу ресурсів, управління інвестиціями [1, 2].

Раніше для розв’язання таких класів задач дослідниками використовувалися різні методи, наприклад, пофарбування графів, методи оптимізації. Але такі підходи не завжди дають уяву про множину розв’язків. Тому виникла потреба створювати такі моделі шаблонів, які б були універсальними структурами і охоплювали б усі варіанти розв’язків задачі.

У науці і практиці застосовують два методи представлення структур і змісту складних систем – графовий і табличний. Саме тому інтерес викликає проблема поєднання моделювання паттернів з теорією графів, зокрема з теорією пофарбування графів. Паттерн описує деякий об’єкт у загальному, використовуючи такі поняття, як “клас”, “властивість”, “атрибут”, “зв’язки” з метою узагальненого вказування на розв’язання проблеми, а граф наочно показує зв’язки між елементами у паттерні, здійснює геометричне, структурне розв’язання даної проблеми. Тому основою побудови парттерна може слугувати задача пофарбовання графа. Багато класів задач зводяться саме до пофарбування графів.

Оскільки методи розв’язування задачі пофарбування графів ґрунтуються у своїй переважній більшості на алгебраїчних операціях над матричним представленням графів, то задачу пофарбування графів зручно формулювати мовою 0-1 програмування. Даний підхід дозволяє формалізувати розглянуті проблеми, застосувати різноманітні оптимізаційні техніки, що враховують у тому числі й накладені обмеження.

Дійсно, можливі представлення багатьох подібних проблем у вигляді системи алгебраїчних рівнянь з невідомими, що є бінарними змінними. Це пояснюється тим, що, по-перше, “природною” мовою для обчислювальних пристроїв є саме представлення чисел у вигляді бінарних масивів, по-друге, розроблено багато математичних пакетів для розв’язування прикладних задач, де ядро математичного процесора оброблює системи алгебраїчних рівнянь також як бінарні масиви.

Подальше дослідження побудови паттернів доцільно зосередити на підходах, запропонованих Абрамсоном, Рандалом, Конолі для пофарбування теоретико-графових моделей.

Так, наприклад, у праці Абрамсона та Рандала [3] наводяться узагальнені алгоритми для розв’язування задач, сформульованих мовою 0-1 програмування. На основі їх алгоритмів розроблено програмний код, що включено до складу багатьох сучасних математичних процесорів, таких як Mathematica, MathCAD, MatLab тощо. Конолі застосував розроблений код для розв’язання багатьох комбінаторних проблем, зокрема у теорії графів для розв’язання задачі про покриття, задачі комівояжера, пофарбування графів.

Вказаними авторами ефективно розв’язувалися економічні задачі, які є типовими задачами, що зводяться до пофарбування графа і побудови паттерна. Зокрема, Конолі та ряд дослідників [4] сформулювали узагальнену задачу розподілу ресурсів (УЗРР).

Нехай для виконання якихось N робіт необхідно розподілити m ресурсів. Вважається, що для виконання і-ої роботи необхідна підмножина ресурсів. Тоді можна побудувати граф G, у якого кожній роботі відповідає деяка вершина графа, а ребро існує у графі лише тоді й тільки тоді, коли для виконання і-ої та j-ої роботи вимагається хоча б один спільний ресурс, тобто . Це означає, що і-та і j-та роботи не можуть виконуватися одночасно. Тоді пофарбування графа G визначає деяке розподілення ресурсів, причому таке, що роботи, які відповідають вершинам одного кольору виконуються одночасно. Мовою 0-1 програмування для УЗРР ці вимоги записуються таким чином:

	(1.1)
	(1.2)
	(1.3)
	(1.4)

Кожний ресурс прив’язаний до конкретної роботи, при цьому ресурси не співвідносяться з однією і тією самою роботою.

Дана проблема є спільною для задач складання розкладів, потокового виробництва, у системах паралельної обробки інформації та розподілених системах. У такому формулюванні дорівнює “1”, якщо і-ий ресурс співвідноситься з j-ою роботою (1.2, 1.3). Змінна дорівнює “1”, якщо і-ий ресурс співвідноситься з j-ою роботою, а k-ий ресурс – з r-ою роботою. Обмеження (1.4) для обумовлює логічні зв’язки між ресурсами.

Відповідний паттерн для класу таких задач можна отримати на основі пофарбування побудованих графів.

Література:

1. De Wera D. An introduction to timetabling / D. De Wera // European Journal of Operations Research. – 1985. – № 19. – P. 151 – 162.

2. Arkin M. Scheduling jobs with fixed start and end times / M. Arkin, B. Silverberg // Discrete Applied Mathematics. – 1987. – № 18.

3. Abramson D. A Simulated Annealing Code for General Integer Linear Programs / D. Abramson, M. Randall // Annals of Operations Research. – 1999. – V. 86, P. 3 – 24.

4. Connolly D. General Purpose Simulated Annealing / D. Connolly // The Journal of the Operational Research Society: Mathematical Programming in Honour of Ailsa Land. – 1992. – V. 43, № 5. – P. 495 – 505.