Болгарина В. И., Колесник С. В.

Национальный технический университет Украины «КПИ»

Моделирование биологических систем с использованием дифференциальных уравнений

Теория дифференциальных уравнений является одним из самых больших разделов современной математики. Она имеет множество связей с разными науками. Огромное применение теория дифференциальных уравнений нашла и в медицине.

Характеризуя математику как метод проникновения в тайны природы, можно сказать, что основным путем применения этого метода является формирование и изучение математических моделей реального мира. Изучая какие-либо физические явления, исследователь прежде всего создает его математическую идеализацию или, другими словами, математическую модель, то есть, пренебрегая второстепенными характеристиками явления, он записывает основные законы, управляющие этим явлением, в математической форме. Очень часто эти законы можно выразить в виде дифференциальных уравнений. Такими оказываются модели различных явлений механики сплошной среды, химических реакций, электрических и магнитных явлений и др.

Применение дифференциальных уравнений в медицине продемонстрируем на примере простейшей математической модели эпидемии. Отметим здесь же, что дифференциальные уравнения в биологии и химии тоже имеют медицинский оттенок, поскольку в медицине важную роль играет исследование различных биологических популяций (например, популяции болезнетворных бактерий) и исследование химических реакций в организме (например, ферментативных).

В модели описывается распространение инфекционного заболевания в изолированной популяции. Особи популяции делятся на три класса. Инфицированный класс численностью x(t) (t — время) состоит из инфицированных (заболевших) особей, каждая из этих особей заразна (предполагается, что инкубационный период заболевания пренебрежимо мал). Второй класс численностью y(t) составляют восприимчивые особи, т. е. особи, которые могут заразиться при контакте с инфицированными особями. И, наконец, третий класс состоит из невосприимчивых особей (приобретших иммунитет или погибших в результате заболевания). Его численность обозначается z(t). Предполагается также, что общая численность популяции n постоянна (т. е. не учитываются рождения, естественные смерти и миграция). Две гипотезы, лежащие в основе модели таковы:

1) заболеваемость в момент времени t равна x(t)y(t) (эта гипотеза основывается на правдоподобном предположении, что число заболевающих пропорционально числу встреч между больными и восприимчивыми особями, которое, в свою очередь, в первом приближении пропорционально x(t)y(t)); таким образом численность класса x растет, а численность класса y убывает со скоростью ax(t)y(t) (a > 0);

2) численность становящихся невосприимчивыми особей (приобретших иммунитет или погибших) растет со скоростью, пропорциональной численности заболевших, т. е. со скоростью bx(t) (b > 0). В результате мы получаем систему уравнения

, (1)

, (2)

. (3)

В силу этой задачи, как легко увидеть, траектории системы (1) – (2) имеют вид, изображенный на рис. 1. (Уравнение (3) теряет свою надобность, поскольку z = n – x – y). Подчеркнем, что нас интересуют только положительные значения переменных.

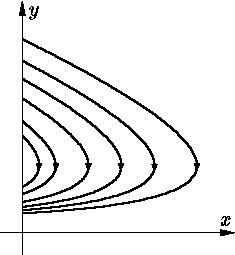
Рис. 1.

Литература:

1. Фурсова П.В., Левич А.П. Математическое моделирование в экологии обществ.

2. Тутубалин В. Н., Барабашева Ю. М. Математическое моделирование в экологии.

3. Олейник О.А. Роль теории дифференциальных уравнений в современной математике и ее приложениях.