Ибрагимов У.М., Баймуратов М.

Южно-Казахстанский государственный университет им. М.Ауезова, Казахстан

К задаче преследования в линейных управляемых системах

Введение. Дифференциальные игры преследования являются математической моделью конфликтных ситуаций, которые возникли в результате математической идеализации технических задач. В таких конфликтных ситуациях обычно имеется два объекта, которые добиваются различных целей. Во всех линейных случаях получены фундаментальные результаты: работы Айзекса, Понтрягина и др [1-2].

В данной работе решается вопрос построения алгоритмов для дифференциальных игр преследования. При этом основными трудностями являются вычисления, так называемой геометрической разности двух множеств. Поэтому, в таких случаях рассмотрены либо эллипсоиды, либо выпуклые многогранники.

Выпуклые множества. Пусть и - два замкнутых выпуклых подмножества пространства , множество

(1)

где и - фиксированные действительные числа, определяется как совокупность всех , где , . Ясно, что выпуклое множество. Очевидно, что если одно из множеств и компактно, то множество замкнуто. Далее, если оба множества и компактны, то множество также компактно. В частном случае, когда , мы получаем алгебраическую сумму двух замкнутых подмножеств пространства .

Геометрическая разность. Если и - два замкнутых выпуклых подмножества пространства , причем компактно, определяется их геометрическая разность

как совокупность всех таких точек , для которых . Ясно, что множество выпукло и замкнуто. Очевидно, что , причем есть максимальное, удовлетворяющее этому условию, т.е. из соотношения

следует соотношение

.

Пусть - замкнутое выпуклое множество, а и - компактные выпуклые множества. Можно показать, что

.

Многозначное отображение. Через обозначим шар радиуса с центром в начале координат в пространстве . Расстояние между двумя компактными множествами и пространства определим как минимальное число , для которого имеют место включения

, .

Так определенное расстояние между множествами и обозначается, как обычно, через . Легко доказывается, что для так введенного расстояния выполняются все аксиомы метрики. Таким образом, совокупность всех непустых компактных выпуклых подмножеств пространства есть метрическое пространство. Очевидно, что , если .

Если есть непрерывная функция действительного числового параметра со значениями в метрическом пространстве то можно определить интеграл

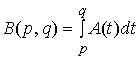
где предполагается, что . При этом оказывается, что есть непрерывная функция пределов интегрирования и . Интеграл определяется как обычный риманов интеграл. Легко доказывается, что выпуклое множество совпадает с множеством всех точек вида

,

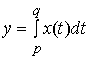где есть такая измеримая функция переменного со значениями в пространстве , что .

Очевидо, что .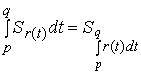

Линейная диференциальная игра. Пусть движение точки описывается уравнением

, , (2)

где - вектор фазовых координат, - управление преследования, - управление убегания; С – квадратная матрица порядка ; и - выпуклые компакты (области управления); Кроме того в пространстве выделено линейное подпространство , которое называется терминальным множеством, на котором игра заканчивается.

Уравнения (2), множества описывает дифференциальную игру двух игроков: преследующего, который распоряжается вектором , и убегающего, который распоряжается вектором . Движение точки начинается при и протекает под воздействием измеримых управлений и на отрезке , .

Будем считать, что измеримые управления выбираются по заданному закону на отрезке , а измеримые управления берется в виде , . Также предполагается, что догоняющий знает уравнение задачи оптимального перехода [3], и множества . Игра считается законченной при допустимых и , , в момент , если при выполнено включение .

Далее, рассмотрим игру (2) с точки зрения догоняющего. Будем считать, что из начального состояния возможно окончание игры преследования, если у догоняющего есть такая стратегия , , что при любом допустимом , , происходит окончание игры на , т.е. хотя бы при одном .

Требуется для заданного начального состояния , ответить на вопрос, возможно ли окончание игры по первому прямому методу Понтрягина [2], если да, то определить гарантированное время преследования , стратегию преследования и траекторию игры при данном , . Конкретная система вида (2), множества и управление , определяются конкретными заданными данными.

Метод Понтрягина для решения линойной задачи преследования. Согласно теореме Понтрягина [2], в игре (2) разрешима задача преследования из позиции , если

1. Множество непусто для ;

2. Хотя бы при одном , .

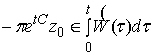Само решение при сделанных предположениях распадается на следующие этапы:

1. Найти множество ;

2. Найти множество ;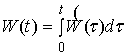

3. Найти , для которого ;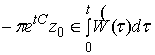

4. Найти функцию такую, что ;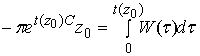

5. Найти как решение уравнения при заданной допустимой , ;

6. Найти как решение уравнения (2) при , , .

В рассматриваемом ниже примере проводятся следующие этапы аналитического вычисления.

Этап 1 - на основании определения геометрическое разности множеств: .

Этап 2 - на основании свойства

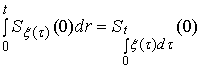
где шар радиуса с центором в нуле, - непрерывная функция ;

Этап 4 - функция выписывается в явном виде

,

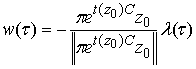где - скалярная функция, выбираемая из условия

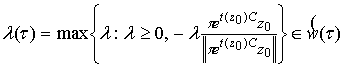
(в изучаемых случаях );

Основными этапами численного решения задачи преследования, являются этапы 3 и 6, заключающиеся в нахождении и последующем нахождении траектории дифференциального уравнения

, , ,.

При построении траектории принят 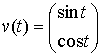. При приведенном варианте где непрерывная функция. Таким образом, есть корень уравнения

Корень следует находить с заданной точностью на отрезке . Если уравнения имеет несколько корней, то предпочтение следует отдать наименьшему из них.

Литература

1. Isaacs, R. Differential Games: A Mathematical Theory with Applications to Warfare and Pursuit, Control and Optimization. New York: Dover, 1999. -384 p.

2. Понтрягин Л.С. Избранные труды. -М.: Наука, 1988. – Т. 2. – 576 с.

3. Ибрагимов У.М. Об одном подходе решения задачи оптимального перехода // Вестник Казах. Нац. Универ. им.Аль-Фараби, -Алматы, сер. мат. мех. инф. №4 (71), 2011. с.48-54.