Джанабердиева С

Математика/Прикладная математика

ӘОЖ 378.016.02:51-8:164.2(574)

К.п.н., доцент Джанабердиева С. А.

Абай атындағы Қазақ ұлттық педагогикалық университеті,

Қазақстан Республикасы, Алматы қ.

PhD докторы, профессор Абудиша Абудула (Abudisha Abudula)

ҚХР, Құлжа қаласындағы Іле мемлекеттік университеті

Магистрант Абдиев А.

Сүлеймен Димирель университеті

Қазақстан Республикасы, Алматы қ.

тарихи мәліметтердің математика сабағына қызықтыру құралы ретіндегі ролі

«Бұған дейінгі мағлұматты білгісі келмей, осы күнгі мен шектелгісі келген адам, оны ешқашан түсінбейді», - деп жазды Г. Лейбниц [1]. Тарихи мəліметтерді математика сабағына енгізу оқушылардың ықыласын арттырып, математиканы тереңірек түсінуге, оқылатын мəліметтерге қызықтыруға, оқушылардың ақыл-ойын кеңітіп, олардың жалпы мəдениетін көтеруге бағыт береді, Қазақстан математикасының тарихымен таныстырады. Мектеп курсының мазмұнына əсері мол тарихи оқиғаларды енгізу арқылы оқушыны маңызды жаңалықтардың тағдырымен, сол жолдағы қиын əрі саналы күреспен, ғылымды таратушылардың аттарымен таныстыру керек» [2]. Алайда, мектеп оқулықтарында математика тарихынан мəліметтер жеткіліксіз, сол себептен тарихи мəліметтер мен бағдарламалық материалдарды жүйелі түрде, үйлестіре отырып баяндау қажет. Тарихи мағлұматтарды пайдаланудың әдістемелері 1-схемада берілді [3].

«Философия көз алдымызда әрқашан ашық тұратын ұлы кітапқа жазылған (мен әлем жөнінде айтып отырмын), бірақ оны, ол жазылған тілді үйренбейінше және ол белгіленген белгілерді ажырата білмейінше, түсінуге болмайды. Ал, ол математика тілінде жазылған және оның белгілері үшбұрыштар, дөңгелектер және басқа математикалық фигуралар» – деп жазды орта ғасырдың ұлы ойшылы Галилео Галилей.

Математика ғылым ретінде есептен пайда болған және есеп арқылы дамиды. Оқушыларды математикаға қызығушылын артыру барысында ойлау қабілетіні дамыту үшін әртүрлі есептердің шығу тарихымен таныстыру керек. Көптеген тарихы мәліметтер есеп түрінде болып келеді.

Тарихи есептер: қызықты тарихи есептер, ежелгі классикалық тамаша бес есеп; шешімі жоқ салу есептері, «жеңілмейтін, берілмейтін», «жауыз есептер», «математиканың көркі», «ұлы», «биік шың», «даңқты» және қазақтың байырғы есептері, қазақтың қара есептері; әсемгерлік есептер т.б. [4].

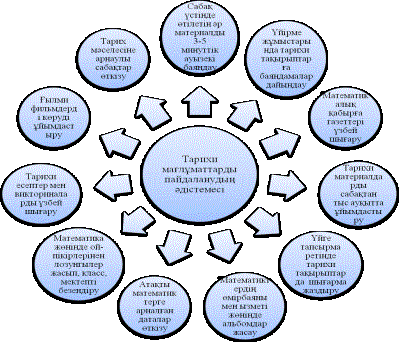
1-схема ─ Математика сабақтарында тарихи мағлұматтарды пайдалану әдістемелері.

Шешімі жоқ (циркуль мен сызғыштың көмегімен салуға болмайтын) тамаша үш есеп: дөңгелекті квадраттау; үшбұрыш трисекциясы; кубті екі еселеу. Кейбір ғалымдар оған тағы екі ежелгі есепті қосады: шеңберді тең бөліктерге бөлу; айшықтарды квадраттау.

Дөңгелекті квадраттау. Дөңгелекті квадраттау (1-сурет.) деп оның ауданын есептеп табуды немесе қандай да бір дөңгелекпен тең шамалы квадратты, әйтпесе дөңгелек шеңберінің ұзындығына тең кесіндіні, салып көрсетуді айтады.

1-сурет - Дөңгелекті квадраттау есебі

Плутарх өзінің «О изгнании» шығармасында баяндауы бойынша, философ және астроном Анаксагор (б.з.б. 500-428 ж) абақтыда отырғанда, дөңгелектің квадратурасы жайлы есепті ойлана отырып өзінің қайғысын ұмытады.

Грек математиктерінің ішінде Архимедке дейін дөңгелекті квадраттау мәселесінде азды-көпті жетістіктерге жеткен: Гиппократ. Қисық сызықтармен шектелген аудандарды квадраттаудың мысалын алғаш рет көрсеткен де осы ғалым. Ол ең алдымен айшық ауданын табу жолын көрсетті.

Мысалы, бір жағынан жарты шеңбермен, екінші жағынан 90 градустық доғамен шектелген «Айшық» үшбұрышымен (яғни жарты дөңгелекке іштей сызылған тең

бүйірлі тік бұрышты үшбұрыштың жартысымен) тең шамалы болатындығын Гиппократ дәлелдеді. Олай болса, мұндай «айшықты» квадраттау мүмкін (2-сурет) екен.

2-сурет - «Айшықты» квадраттау есебі

Дөңгелекті квадраттау проблемасын циркуль және сызғыштың көмегімен шешу мүмкін еместігі біздің заманымызда дәлелденді.

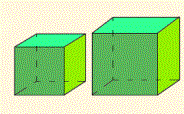
Кубті екі еселеу. Бұл есеп алгебралық жолмен келесі куб теңдеуді шешуге келіп тіреледі, бұл теңдеуге келтірген орта азиялық математик Омар Хайям болған.

Біздің жыл санауымыздан бұрын V ғасырда геометриялық алгебра тәсілімен шешуге келмеген проблемалардың бірі «кубты екі еселеу туралы» проблема болды (3-сурет). Бұл ежелгі грек математиктерінің үшінші классикалық есебі осылай аталады: көлемі берілген кубтың көлемінен екі есе артық болатын куб құру керек. Сөйтіп бұл кубтардың көлемдерінің қатынасы 1 мен 2-нің қатынасындай болу керек. Қазіргі математика тілімен айтқанда, үшінші дәрежелі теңдеуін шешу керек немесе бәрібір санын геометриялық жолмен құру керек. Сөйтіп, көлемі -қа тең кубтың қырын циркуль және сызғыштың көмегімен құру керек. Бұл есепті шешу мүмкін еместігі XIX ғасырдың 30 жылдарында дәлелденді.

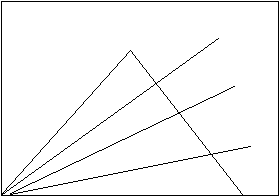
-тан өзге сүйір бұрыштың трисекциясы. Циркуль және сызғыш көмегімен бұрышты үш тең бөлікке болу жайында Платон: «құралдар неге сонша шектелген» деген екен, себебі бұл шешімі жоқ салу есептерінің бірі. Математика тарихы жайындағы кітаптарда бұл есеп «бұрыштың трисекциясы» (4-сурет) деп атайды.

Есептің атын өзгерткен себебіміз: есепті -тық бұрыштарда шешуге болатындығында.

3-сурет – Кубті екі еселеу есебі

4-сурет – бұрыштың трисекциясы

1. Салу есебі: -тың трисекциясы. Өлшемі -тық тік бұрыштың трисектрисасын салу үшін әуелі тік бұрыштың ішкі бөлігіне бір катетімен қабырғалас өлшемі -қа тең бұрыш салып алып (тең қабырғалы дұрыс үшбұрыштың бұрыштары-қа тең), осы -тық бұрыштың биссектрисасын саламыз. Сонда -тық бұрыштың трисекциясы шығады, яғни ол -тан тең үшке бөлінеді (5-сурет).

5-сурет – Тік бұрыштың трисекциясы

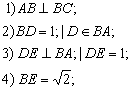
2. Салу есебі. -тың трисекциясының басқа әдісі: теңдігін пайдаланамыз.

Салу:

5)Шеңбер;

6) Шеңбер;

9)Шеңбер

10) Шеңбер

11)

12)

13) Тік бұрышты

14)

15) биссектриса;

16) және - ізделінді трисектрисалар.

3. Салу есебі: -тың трисекциясы. -тық бұрыштың биссектрисасын саламыз. Алынған-тық бұрыштың трисекциясын салу міндетіміз. Ол үшін -тық тік бұрыштың ішкі бөлігіне бір катетімен қабырғалас өлшемі -қа тең бұрыш салып алып (тең қабырғалы дұрыс үшбұрыштың бұрыштары -қа тең), осы -тық бұрыштың биссектрисасын саламыз. Алынған -тық бұрыштың биссектрисасын саламыз. Сонда өлшемі -тық бұрыш аламыз. -тық бұрыштың бір қабырғасынан -тық бұрышты үш рет өлшеп саламыз. Сонда -тық бұрыштың трисекциясы шығады, яғни ол -тан тең үшке бөлінеді (6-сурет).

6-сурет – -тық бұрыштың трисекциясы

Жазықтықтағы әртүрлі салу есептері.

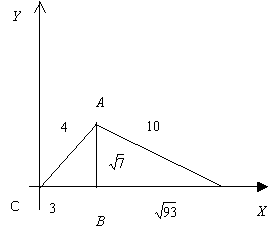
4. Салу есебі. Ұзындығы кесіндісін салу есебі. Тік бұрышты координаталар

жүйесінде центрі бас нүктеде (О нүктесінде), ал радиусы 3 бірлік кесіндіге тең шеңбер сызамыз (7-сурет).

Салу:

1) Шеңбер; |;

2) Шеңбер;

3) ;

4) Шеңбер;

5) Шеңбер; | ;

6) Шеңбер ;

7) Шеңбер;

8) – ізделінді кесінді.

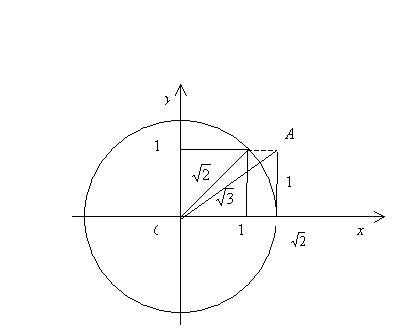
7-сурет

5. Салу есебі. кесіндісін салу (8-сурет). Ізделінді кесінді .

8-сурет– Ұзындығы кесіндісін салу есебі

Жазықтықтағы классикалық салу есептері.

1. Кесіндіні қақ бөлу есебі;

2. Түзуден тысқары жатқан нүктеден сол түзуге перпендикуляр салу есебі;

3. Түзудің бойында жатқан нүктеден сол түзуге перпендикуляр салу есебі;

4. Берілген қабырғалары бойынша үшбұрыш салу есебі;

5. Бұрыштың биссектрисасын салу есебі;

6. Медианалары бойынша үшбұрыш салу есебі;

7. Центрі берілмеген шеңбердің центрін табу есебі;

8. Шешімі жоқ есептер; т.б.

Шеңберді тең бөліктерге бөлу. Шеңберді тең бөліктерге бөлу себебі дұрыс көпбұрыштың салу есебімен тікелей байланысты: дұрыс көпбұрыштарды салу есебі ерте кездегі салу есептердің қатарына жатады. Бұған дәлел Пифагор мектебінде циркуль мен сызғыштың көмегімен қабырғаларының саны мұндағы n=1,2,3... болатын дұрыс көпбұрыштарды сала білген.

Айшықтарды квадраттау. Б.з.б. V ғасырда ежелгі грек математигі Гиппократ айшықтарды квадраттау көп көңіл бөледі.

Қазақтың байырғы қара есептері: әр ғасырда өмірге келіп, қазақ ауылының тыныс-тіршілігін, әл-ауқатын, өмірге араласуын, мақсатқа жету ізін, философиялық күрмеуін, қазақ халқының тәлімінің сыр-сипатын бейнелейді.

Қазақтың қара есептері. Қазақ халқының математикалық білімінің қолданыс жағы басымдау. Ол осынысымен құнды. Қазақ педагогикасының математикалық астарлары да түрліше. Олар біресе жұмбақ, біресе өлең, біресе қара сөз, біресе ертек, біресе ілмек, біресе дұзақ, біресе ұйқас табу, біресе мақалдап сөйлеу, біресе ұсақ заттармен өнер көрсету, біресе сиқырлы ой айту, біресе тұрмыс заттарын жасау түрінде кездеседі.

Әсемгерлік есептер. Алтын қимамен байланысты есептер.

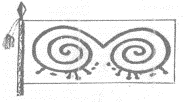
«Алтын қимамен» кесу есебі. Б.з.б 2500-2000 жыл шамасындағы Қазақстан жерінде өмір сүрген ата-бабаларымыз көк тәңірін бас бітімі қос шеңберден тұратын күн тәжі адам пішіні арқылы таңбалап көрсеткен (9-сурет).

Бұл күнтәжілі хақтәңірдің суретіндегі мыс дәуірінде салынған спираль сызықтар мен нүктелерден сол кездегі адамдардың әлем құрылысы туралы түсінігі мен есептеу әдістері жайында белгілі бір болжамдық ойлар айтуға болады. Бейнелік белгінің бірі ту белгісі боп саналады. Сондықтан тас бетіне күн мен түннің теңелген сәтінің бейнесі – қошқар мүйізді қос «алтын спиральды» ою салған «алтын тіктөртбұрыш» кілемшені жаңа жыл жалауы – «Наурыз туы» (10-сурет)-деп қарастыруға болады.

9-сурет. Мыс дәуіріндегі «Күн тәжілі» тәңірхақ.

10-сурет - «Алтын жалау» - әсемдік туы

Ұнасымдық пен үздіксіздіктің үйлесімі – әсемдік туы, «Алтын кесіндіні», «алтын төртбұрышты» бейнелейтін санымен байланысты.

Шехеризада фокусы [5]. 1001 – Шехеризада саны деп аталады. 1001 саны, 7, 11 және 13 сандарына қалдықсыз бөлінеді немесе болады. Кез келген үш таңбалы санды 1001-ге көбейткенде шығатын көбейтінді - осы үш таңбалы санды екі рет қайталап жазғанға тең: немесе .

Осы санның көмегімен «ойлаған санды табу» есебін шығарып көрейік. Ол үшін бірінші оқушыға үш таңбалы сан ойлау ұсынылады. Оны қағазға жазғаны дұрыс. Енді ойлаған санға осы санның өзін тіркеп жазып, сан жазылған қағазды екінші оқушыға береді. Екінші оқушы қағазға жазылған санды 13-ке бөліп, шыққан санды үшінші оқушыға береді. Үшінші оқушы 13-ке бөлінген санды 11-ге бөліп, төртінші оқушыға беруі керек, ал төртінші оқушы 11-ге бөлінген санды 7-ге бөліп, шыққан санды оқуы керек. Бұл сан бірінші оқушының ойлаған саны болады. Мұнда ешқандай да құпия жоқ. Үш таңбалы бір сан ойлап, оны 1001-ге көбейтіп, қайта 1001-ге бөлдік. Нәтижесінде ойлаған санның өзі шықты.

Ойынды мысалмен көрсетейік: Бірінші оқушы 871 санын ойлады дейік, оған 871 санын тіркеп 871871 түрінде жазып, екінші оқушыға берді делік. Бұл -ге көбейтілгенде 871871 саны шығады. Екінші, үшінші, төртінші оқушының кезегімен 13, 11, 7-ге бөлуі, бұл санды 1001-ге бөлумен тең. Себебі, санын береді. Сонымен, 871 санын 1001-ге көбейтіп, қайта 1001-ге бөлгенде, бөліндіде ойлаған 871 саны шығады. Бұл саннан басқа да үш таңбалы кез келген сан ойлап, ойынды жалғастыруға болады.

Қызықты тарихи есептер оқушылардың математиканы оқып үйренуіне қызығушылығын тудырып, алған білімдерін өмірге қолдана білуге тәрбиелейді.

Әдебиеттер

1. Глейзер Г.И. Мектептегі математика тарихы / IV-VI кластар үшін оқу әдістемелік құрал – Алматы, 1985.

2. Программа по математике для V-VI средней общеобразовательной школы / Математике в школе – 1985 - № 6.

3. Сабалақов А. Математика тарихынан. – Алматы: Мектеп, 1966 – 176-179 бб.

4. Белозеров С.Е. Пять знаменитых задач древности. – Ростов: Ростовский университет, 1975.

5. Жұмабекова Р. Ә. «Киелі сандар сыры және жай сандар туралы» - [Электорондық ресурс]. - Сайттқа жету режимі: http://www.mathematik.ucoz.kz/conf2010/works/n-dir-li_a..doc

SUMMER

This paper examines the role of historical materials in mathematics lessons as a means of entertaining. Are a few classic historical problems. The possibility of constructing trisection of some angles and suggest methods for their construction. The contradiction of the failure of historical materials in mathematics textbooks today. Suggested the need to offer historical references in the system consistency and compliance with program material.