Таттибеков
К.С.
Таразский
государственный педагогический институт, Казахстан
Анализ солитонов в одной двумерной модели магнетиков
Обнаружение нелинейных подвижных
протяженных объектов как в теоретических моделях, так на экспериментальном
уровне стало одним из основных глобальных событий в физике последних десятилетий,
и сейчас термин "солитон", означает целый класс нелинейных объектов,
на которые возлагаются большие надежды как на ключ для решения ряда самых
актуальных физических проблем.
Стабильность солитонов, кинков и других
частицеподобных кластеров часто оказывается связанной с существованием
дополнительных (ненетеровых) законов сохранения так называемых
"топологических зарядов", которые в ряде случаев могут принимать
только дискретные значения, и связаны с глобальными характеристиками
многообразия полевых конфигураций. Часто
солитоны стабилизируется наличием интегралов движения типа $E, $P и $N. Такие
солитоны называются динамическими и существуют как стационарные состояния
только в меру сохранения величин E, P, N.
Если включить в уравнения движения сколь угодно малые возмущения, разрушающие
эти интегралы движения, то динамические солитоны могут быть ликвидированы, и
возбужденный магнетик будет переведен в основное состояние. При этом переход магнетика из возбужденного состояния в
основное сопровождается непрерывной деформацией поля намагниченности. Иногда говорят, что динамический солитон
топологически эквивалентен основному состоянию. Например, неоднородное
состояние одномерного ферромагнетика топологически эквивалентно основному.
Одномерное решение уравнений Ландау-Лифщица, как бы
соединяющее два вакуума, описывает такое неоднородное состояние
намагниченности, которое никакими конечными деформациями поля намагниченности
не может быть сведено к основному[1]. Подобные решения принято называть топологически особыми, им отвечают
топологические солитоны. Примером таких топологических солитонов является
кинки.
Одной из физически важных нелинейных моделей двумерных
магнетиков является (2+1)-мерное обобщенное уравнение Ландау-Лифщица (ОУЛЛ) следующего вида [2,3]:
![]() , (1)
, (1)
где ![]()
![]() - матрица
анизотропии, причем
- матрица
анизотропии, причем ![]() ,
, ![]() - некоторая вектор-функция.
- некоторая вектор-функция.
В изотропном случае (![]() ) ОУЛЛ (1) принимает вид
) ОУЛЛ (1) принимает вид
![]() . (2)
. (2)
Введем стереографическую проекцию спинового вектора ![]() согласно
формулам [1]:
согласно
формулам [1]:
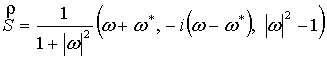 ,
,
где ![]() является комплексной
функцией. В терминах новой комплексной
переменной
является комплексной
функцией. В терминах новой комплексной
переменной ![]() , и при подходящем
выборе
, и при подходящем
выборе ![]() уравнение (2)
принимает вид
уравнение (2)
принимает вид
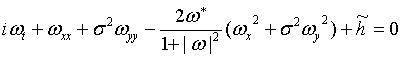 . (3)
. (3)
Здесь h некоторая комплексная функция.
Решение поставленной задачи построено в работе [4] в
виде
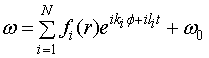 , (4)
, (4)
где ![]() и
и ![]() является целыми числами,
является целыми числами, ![]() - некоторая комплексная константа, из
которого получаем следующее представление
- некоторая комплексная константа, из
которого получаем следующее представление
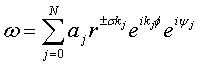
где ![]() и
и ![]() .
.
Далее анализируем полученные решения. Рассмотрим
топологический заряд этих решений. Соответствующее число наматывания обхода
может быть вычислено с помощью формулы
![]() .
.
Вспомним, что топологический заряд любого
рационального отображения ![]() , где
, где ![]() есть полином, равен степени этого полинома. Выражение
(4) также является полиномом, так что
есть полином, равен степени этого полинома. Выражение
(4) также является полиномом, так что
![]()
Заметим, что полный топологический заряд этих решений
фиксируется асимптотически ведущим членом, т.е. наибольшим значением ![]() . В тоже время
локальное распределения топологических солитонов зависит от всех чисел
. В тоже время
локальное распределения топологических солитонов зависит от всех чисел ![]() . В самом деле, если
рассмотреть эти решения при больших
. В самом деле, если
рассмотреть эти решения при больших ![]() , то векторное поле
, то векторное поле ![]() раз наматывается вокруг начала координат. Как
мы обсудим ниже, наша конфигурация проявляется как
раз наматывается вокруг начала координат. Как
мы обсудим ниже, наша конфигурация проявляется как ![]() солитонов с топологическими зарядами
солитонов с топологическими зарядами ![]() , где
, где ![]() зависит от чисел
зависит от чисел ![]() и
и ![]() . Полным зарядом
является сумма
. Полным зарядом
является сумма ![]() индивидуальных зарядов
индивидуальных зарядов
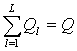 .
.
Найдем позицию солитонов. Она определяется как решение
следующего условия:
![]() .
.
Таким образом, точки локализации солитонов
определяются уравнением
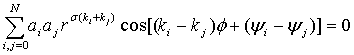 . (5)
. (5)
К сожалению,
не удается построить точные аналитические решения этого уравнения для
произвольных ![]() . При
необходимости можно построить численное
решение этого уравнения для любого заданного значения
. При
необходимости можно построить численное
решение этого уравнения для любого заданного значения ![]() . В данной работе найдены точные аналитические решения в двух
простейших случаях: при
. В данной работе найдены точные аналитические решения в двух
простейших случаях: при ![]() и
и ![]() .
.
а) Случай
![]() . При
. При ![]() уравнение (5) примет
вид
уравнение (5) примет
вид
![]() .
.
Мы видим, что здесь существуют ![]() солитонов, каждый из
которых имеет единичное топологическое число
и локализованы на круге с
радиусом
солитонов, каждый из
которых имеет единичное топологическое число
и локализованы на круге с
радиусом
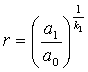 ,
,
в точках 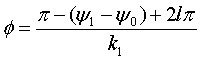 ,
,
где ![]() .
.
б) Случай ![]() . Случай
. Случай
![]() является более
интересным и содержательным. Пусть
является более
интересным и содержательным. Пусть ![]() . Тогда уравнение
(5) принимает вид
. Тогда уравнение
(5) принимает вид
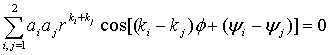 .
.
В этом случае солитоны локализованы в следующих
точках
![]() ,
, 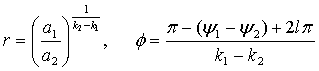 ,
,
где ![]() . Здесь имеется два типа солитонов. Первый находится в начале
координат с числом витков равным к min
. Здесь имеется два типа солитонов. Первый находится в начале
координат с числом витков равным к min![]() . Вокруг этого солитона находится
. Вокруг этого солитона находится ![]() сателлитных солитонов
с единичным топологическим зарядом.
сателлитных солитонов
с единичным топологическим зарядом.
Литература:
1. Косевич А.М., Иванов Б.А., Ковалев А.С. Нелинейные
волны намагни-ченности. Динамические и топологические солитоны. –Киев:Науково
Думка, 1983.-192 с.
2.
Ferrer R. /Phys.Pev., 1989, B40,№16, p.1107.
3. Тунгатаров А.Б., Нугманова Г.Н., Мырзакулов Р.
Интегрируемые обоб-щенные уравнения Ландау-Лифщица/ Евразийский математический журнал, 2005, №2, с.33-40.
4. Таттибеков К.С. Солитоны в одной изотропной модели магнетиков / Материалы VIII международной научно-практической
конференции «Новейшие научные достижения»,Т31, Математика, София,2012,с.3-7.