Математическое моделирование задачи устойчивости водонасыщенного склона

 

Дана Ермухамед, студентка 3 курса КазНУ им. Аль-Фараби, г.Алматы

                  

               Научный руководитель: д.т.н., проессор.КазГосЖенПУ  Р.Б.Баймахан

 

            Ежегодно в мире происходят большие оползни на склонах холмов, унося  человеческие жизни и нанося огромные ущербы народному хозяйству. Причины их разные, некоторые из них могут быть связаны с техногенной деятельностью человека, иногда при землетрясениях. Здесь, наверное, уместно привести два-три таких факта, которые произошли в окрестностях г.Алматы. К территории города примыкают цепочки высоких холмов и горных склонов. В последние годы на юго–восточной части города нависла угроза крупного оползня склонов высокого холма Коктобе. К сожалению весной и летом 2004 года эта угроза реализовалась в виде последовательно произошедших оползней в районе села Акбулак между городами Алматы и Талгар и на западе южной столицы, разрушивших дома жильцов, дачников и санаторные здания заживо погребавших под собой 29 человек на юге и 2 – на западе. Вопрос обеспечения устойчивости склонов ­– сама по себе задача проблемная.  Иногда оползни перекрывают транспортные дороги, проложенные у подножий холмов или на склонах между холмами. Во всех этих случаях главной причиной протекания оползней по видимому является водонасыщенность грунтов на склонах. Поэтому этот вопрос всегда остается проблемой.

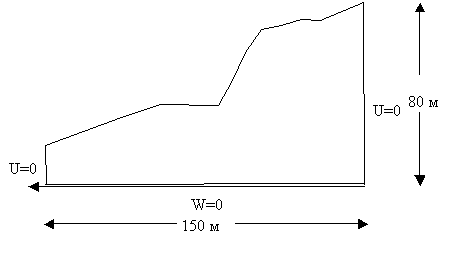
            Ниже предлагаются результаты счетов по определению устойчивости (напряженного состояния) склона с защитным сооружением в упругой постановке. Геометрические размеры области и граничные условия показаны на рисунке 1.   

                                                                                                                       Z          

 

 

 

 

 

 

 

 

 

 


                                    X

                                

 

Рисунок 1.  Форма склона, геометрические размеры и граничные условия.

 

            Для  конечноэлементного моделирования указанной выше области здесь удобно применять линейного четырехугольного изопараметрического элемента произвольной формы, но с дополнительными внутренними точками интегрирования.

       Декартовые координаты  узлов и составляющие их перемещений с местными координатами связаны через функции форм  в виде /1/:

                            ,                      .                                                (1)

                            ,                      .                                               (2)

 

На рисунке 2 показан четырехугольный элемент в координатах  и .

 

 

 

 

 

 

 

 

 

 

 

 


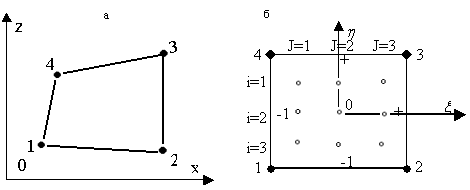
Рисунок 2. Четырехугольный расчетный элемент первого порядка. а – 

 

 

Для четырех его вершин справедливы следующие функции :

 

                                          (3)

 

где , . Подставив (3) в (1) и (2), можем вычислить декартовые координаты любой точки и их перемещения. Компоненты деформации в матричной форме будет иметь вид

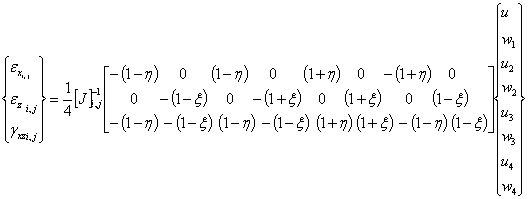           (4)

Матрицу жесткости элемента составляем по обычному правилу МКЭ в виде

 

                                        .                               (5)

где i,j – толщина элемента в точке .  – матрица упругих характеристик материала,  - весовые коэффициенты для точек интегрирования, –матрица градиента входящая в (4).

            Теперь приведенные модуль упругости , коэффициент Пуассона , которые входят в  матрицу упругости  для водонасыщенного грунта вычисляются выражениями /2/:

                                                ,       ,                          (6)

где и - модуль объемного сжатия “грунтовой массы”;  

где  – доли объемных содержаний в грунте твердой и жидкой (газонасыщенной) компонент ( , ,  , для воды  Мпа, , модуль Пуассона и модуль упругости твердой компоненты соответственно). Индексы , , соответствуют твердому включению,  грунту и водной компоненте.

            Известное в МКЭ уравнение равновесия запишем  в виде

                                                                                                                                             ,             (7)

 

где матрица жесткости системы, которая формируется суммированием жесткостей элементов  отдельных элементов окружающей  узел. Вектора ,  – силы от собственного веса горного массива и неизвестные узловые перемещения.

            Для решения уравнения равновесия (7) матрицу  представим в виде произведения нижней  и верхней треугольных матриц.

 

                                               ,                                                                         (8)

здесь

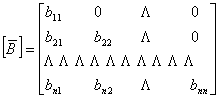                           и  .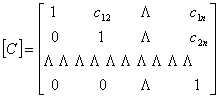

 

Элементы этих матриц  и  определяются в виде .

 

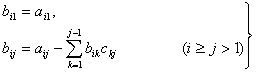                                                                                (9)

и

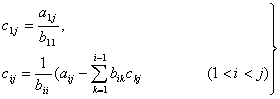                          .                                               (10)

 

Отсюда искомый вектор  определяется в результате последовательного решения следующих систем уравнений.

 

                                               ,

                                               .                                                                           (11)

 

Так как матрицы  и  имеют треугольную форму, то эти системы решаются очень просто с помощью следующих алгоритмов.

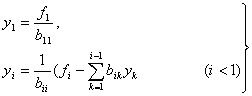                                                                                 (12)

и

 

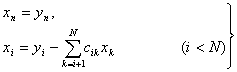                                                                                     (13)

Заметим, что здесь выгрышно вычислять параллельно  и  в уравнениях (11)

            Так как  матрица  симметрична, то есть , тогда

                                                                                                                       (14)

Вектор составляющих  напряжений вычисляется с помощью выражения:

                                                                                                                                                                                 ,          (15)

где –  составляющие напряжений.

            В данном сообщений 1 с помощью изложенного алгоритма (1) – (15) изучено напряженное состояние  неводонасыщенного склона (, m=0) показанного на рисунке 1. Геометрические размеры расчетной области показаны на рисунке 2. Для расчета приняты следующие значения физико механических свойств: модуль Юнга – ; коэффициент Пуассона –  и объемный вес . В качестве нагрузки выступает геостатическая сила от собственного веса массива – .

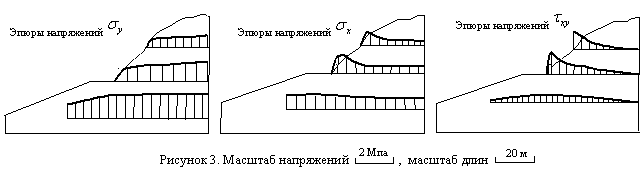
            На рисунке 3 показаны эпюры напряжений ,  и  для различных глубин от свободной поверхности склона. Значения с глубиной увеличивается и уменьшаются с приближением к свободной поверхности. Величины с приближением к свободной поверхности склона увеличиваются. Величины касательных напряжений на  поверхности склона также увеличиваются. В удаленных точках от земной поверхности в глубине массива касательные напряжения уменьшаются.

 


           

 

 

 

 

 

 

 

 

 

РЕЗЮМЕ

                В данной статье рассмотрена математическая модель исследования устойчивости водонасыщенного склона.

 

Литература

1. Зенкевич О. Метод конечных элементов в технике. М., Мир, 1975, 541с.

2. Красников Н.Д. Сейсмостойкость гидротехнических сооружений из грунтовых 

    материалов. М., Энергоиздат, 1981. 240с.