УДК 631.4.53
Разработка регрессионных
математических моделей процессов засоления и рассоления мелиоративных почв
юго-востока республики казахстан
Калдыбаев С.К., Бакенова Ж.Б.
Казахский
национальный аграрный университет, г.Алматы (Казахстан)
Изучение взаимодействия между физическими, химическими и биологическими процессами засоления почв, проведенное в натуральных условиях, позволило собрать и обобщить многолетние данные наблюдений над их состоянием, разработать и провести исследование этих процессов на математических моделях.
Для обработки и анализа опытных данных о засолении почв использованы методы прикладной математической статистики, среди которых можно выделить дескриптивную (описательную) статистику, парные критерии, анализ факторных эффектов, дисперсионный, корреляционный и регрессионный анализ, а также многомерные методы сравнения. С этой целью результаты экспериментальных исследований были представлены компьютерной информационной базой данных о засолении почв и её динамике в зависимости от внесенных доз фосфогипса и промывки. Совокупность опытных данных, характеризующих количественно процесс засоления почв, была сведена в таблицы этой базы данных. В каждой строке такой таблицы содержится результаты каждого наблюдения над суммой солей и соответствующими компонентами засоления Ca2+, Mg2+, Na+ и K+, которые находятся в некоторой зависимости по отношению друг к другу.
В качестве зависимых переменных выбраны компоненты засоления Ca2+, Mg2+, Na+ и K+, отражающие состояние почвенно-поглощающего комплекса. Уровень компонентов Ca2+, Mg2+, Na+ и K+ при различных значениях аргументов D, H и T необходимо было исследовать и предсказать по имеющимся экспериментальным данным.
Обработка опытных данных и расчеты проводились на компьютере с использованием программного обеспечения научных исследований. Профессиональные статистические пакеты программ SPSS 11.5, Statisticа 6.0 и Statgraphics 5.0 для Windows [1-5], а также надстройка «Анализ данных» офисной программы Excel [6-7] позволили оценить выборочные характеристики, провести анализ и проверку гипотезы о законах распределения исследуемых показателей Ca2+, Mg2+, Na+ и K+, построить статистические графики и регрессионные модели почвенно-поглощающего комплекса.
Опытные данные обрабатывались с учетом предпосылок и требований корректного применения методов статистического моделирования.
Двумерный анализ показателей Ca2+, Mg2+, Na+, K+ основанный на точечных диаграммах рассеяния, мерах связи – коэффициентах корреляции (для линейных зависимостей) и корреляционных отношениях (для криволинейных закономерностей), а также критерии линейности позволили выявить тенденции изменения показателей засоления и рассчитать для них адекватные уравнения регрессии.
На рисунке 1 приведены закономерности изменения уровня засоления почв в
результате промывки водой. Кривая изменения суммы солей до промывки (Sдп)
лежит значительно выше (в полосе 1,8–2,4), чем кривая суммы солей после промывки
почв (Sпп).
При математическом описании таких двумерных зависимостей и аппроксимации опытных данных используют, в основном, линейную, экспоненциальную, мультипликативную, гиперболическую и другие функции, которые могут быть линеаризованы по оцениваемым параметрам. Для характеристики корреляции при криволинейных зависимостях теснота связи между факторами и результативным показателем измеряется корреляционным отношением η. Величина η меняется от 0 до 1. Чем ближе значение η к 1, тем выше взаимосвязь переменных, тем точнее она описывается используемой для аппроксимации криволинейной зависимостью.
В результате использования метода
пошаговой регрессии Stepwise
с указанными выше параметрами получены следующие модели солевого
состава почв:
![]() (1)
(1)
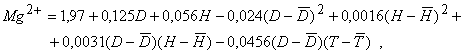 (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
В целом на величину компонентов ППК существенное влияние оказывает доза внесенного фосфогипса D. Исключение составляет K+. Формирование K+ в большей степени зависит от глубины H, с увеличением которой значения K+ уменьшаются, и времени протекания процесса T, в течение которого происходит накопление K+. В модели регрессии (1)–(4) вошли как статистически значимые линейные члены D, Н, Т, квадратичные эффекты и парные взаимодействия некоторых центрированных величин факторов D, Н, Т.
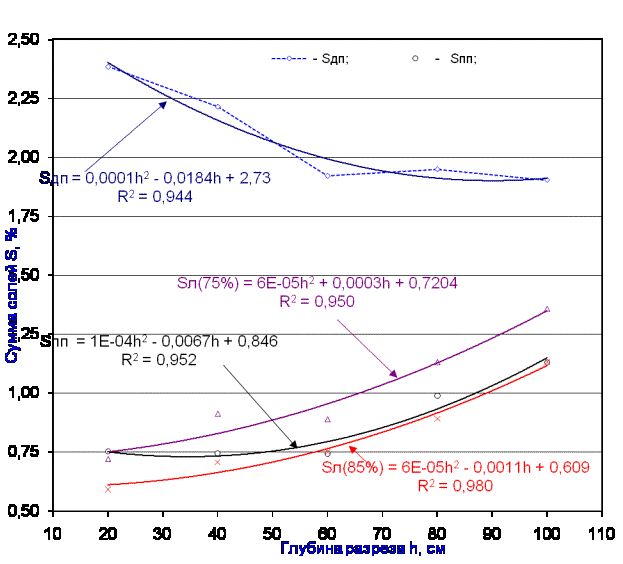
Рис. 1. Изменения уровня засоления почв при промывке водой
В результате расчета получены следующие многофакторные модели для компонентов почвенно-поглощающего комплекса:
Сa2+ = 7,78–0,33Mg2+–0,366Na++0,055D–0,06H+0,01![]() +0,02
+0,02![]() ; (5)
; (5)
Mg2+ = 7,98–0,279Сa2+ –0,545Na+ –0,704K+ +0,066D+0,021H–0,0072![]() +
+
+ 0,141![]() + 0,003
+ 0,003![]() –
0,0414
–
0,0414![]() ; (6)
; (6)
Na+ =
9,32 – 0,35Сa2+ – 0,66Mg2+ – 0,52K+ – 0,102T + 0,085![]() +
+
+ 0,0065![]() –
0,0012
–
0,0012![]() + 0,129
+ 0,129![]() –
–
– 0,025![]() +0,44
+0,44![]() +0,216
+0,216![]() –
–
– 0,083![]() –
0,074
–
0,074![]() + 0,033
+ 0,033![]() ; (7)
; (7)
K+ =
4,28–0,258Mg2+ –0,169Na+ +0,129![]() +0,007
+0,007![]() +
+
+0,06![]() +0,015
+0,015![]() . (8)
. (8)
В соответствии с абсолютной величиной t-критериев переменным,
вовлеченным в регрессионные модели (5)–(8), присвоены ранги, упорядочивающие
члены регрессии по степени их воздействия на соответствующую выходную
компоненту Ca2+,
Mg2+,
Na+ и
K+. Высокие
ранги (1, 2 и 3) в модели для Ca2+ имеют H, Na+
и Mg2+,
для Mg2+
– Na+,
K+ и D, для Na+
– Mg2+,
Ca2+
и парное взаимодействие ![]() , для K+ – Mg2+,
, для K+ – Mg2+, ![]() и Na+.
и Na+.
Чтобы оценить качество разработанных регрессионных моделей засоления почв (1)–(4) и (5)–(8), рассчитаны коэффициент множественной корреляции R, детерминации R2, критерий Фишера F с оценкой его значимости p и критерий Дарбина-Ватсона d (таблицы 1 и 2).
Таблица 1-Оценка адекватности моделей почвенно-поглощающего комплекса вида
|
Компоненты
|
Статистические показатели и критерии
адекватности |
||||
|
R |
R2 |
F |
p |
d |
|
|
|
Метод
Enter |
||||
|
Ca2+ |
0,906 |
0,821 |
45,954 |
<0,001 |
1,813 |
|
Mg2+ |
0,832 |
0,693 |
22,563 |
<0,001 |
2,277 |
|
Na+ |
0,695 |
0,483 |
9,342 |
<0,001 |
2,146 |
|
K+ |
0,642 |
0,413 |
7,022 |
<0,001 |
1,877 |
|
|
Метод Stepwise |
||||
|
Ca2+ |
0,899 |
0,808 |
79,326 |
<0,001 |
1,786 |
|
Mg2+ |
0,826 |
0,683 |
33,358 |
<0,001 |
2,260 |
|
Na+ |
0,683 |
0,466 |
16,394 |
<0,001 |
2,123 |
|
K+ |
0,609 |
0,370 |
18,830 |
<0,001 |
1,743 |
Полученные многомерные регрессионные зависимости (1)–(4) показателей Ca2+, Mg2+, Na+ и K+ от внесённой в почву дозы фосфогипса D, глубины H и продолжительности T достаточно полно характеризуют исследуемый процесс. Коэффициент множественной корреляции колеблется от 0,98 до 0,99, критерий Фишера от 14,9 до 946, что показывает достоверность и высокую адекватность полученных моделей.
Y=f(D,H,T)=f(X1,X2,X3)=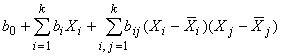
Таблица 2- Проверка
качества моделей почвенно-поглощающего комплекса, учитывающих взаимодействия
компонентов Ca2+,
Mg2+,
Na+ и
K+
|
Статистические
показатели |
Компоненты ППК |
|||
|
Ca2+ |
Mg2+ |
Na+ |
K+ |
|
|
Множественный
коэффициент корреляции R |
0,922 |
0,918 |
0,915 |
0,763 |
|
Коэффициент детерминации R2…………. |
0,849 |
0,943 |
0,838 |
0,582 |
|
Критерий Фишера F……………………… |
87,299 |
53,737 |
31,302 |
21,572 |
|
Число степеней свободы df : k1; k2………. |
6; 93 |
9; 90 |
14; 85 |
6; 93 |
|
Значимость F……………………………... |
<0,001 |
<0,001 |
<0,001 |
<0,001 |
|
Критерий Дарбина-Ватсона d ……….….. |
1,765 |
2,312 |
2,231 |
1,802 |
Модели почвенно-поглощающего комплекса (5)–(8), полученные методом Stepwise из полных регрессионных уравнений, хорошо аппроксимируют исходные опытные данные, учитывая при этом от 58% для K+ и до 94% для Mg2+ (таблица 2) вариации выходных показателей. Модели имеют высокую достоверность и статистически значимый F-критерий Фишера на уровне p<0,001 для всех построенных функций отклика Ca2+, Mg2+, Na+ и K+.
При построении моделей (5)–(8), зависящих от трех переменных (D, H и T), получены n=100 остатков, по которым рассчитаны
значения критерия d (таблица 1). Для n=100, q = 0,025 и k=3 имеем табличные значения dL
и dU по Дарбину
и Ватсону: dL =
1,55 и dU =1,67. Сопоставляя
приведенные в таблице 52 значения d критерия Дарбина-Ватсона с границами следующих неравенств
dU < d < 4 –
dU
или 1,67 < d < 2,33
приходим к выводу, что эти неравенства выполняются для всех моделей. Следовательно, проверяемая нулевая гипотеза принимается на 5%-ном уровне значимости. Рассчитанные значения критерия Дарбина-Ватсона d незначимы, а сериальная корреляция действительно отсутствует в наших данных.
Итак, проверка наличия сериальной корреляции в регрессионных остатках наряду с другими статистическими критериями (F, R, R2) показала высокую информативность и достоверность полученных моделей почвенно-поглощающего комплекса (1)–(4) и (5)–(8), а также процессов засоления-рассоления почв. По этим моделям можно построить статистически обоснованный прогноз исследуемых компонентов ППК и процесса засоления-рассоления почв в целом. Такого рода задача может быть решена с помощью методов корреляционного, спектрального или авторегрессионного анализа, позволяющих выявить периодические процессы в поведении временных рядов.
Разработанные регрессионные модели применимы также к временным рядам и к любым другим типам наблюдаемых зависимостей компонентов ППК от одной или нескольких переменных D, H, T. Такие модели позволяют не только построить прогноз, но и определить оптимальную область переменных D, H, T, например, – оптимальную дозу вносимого в почву фосфогипса или водной промывки, за которой дальнейшие затраты на такие методы рассоления почв уже не принесут пропорционального эффекта.
Список литературы:
1.
Боровиков В.П., Боровиков И.П. Statistika
- Статистический анализ и обработка
данных в среде Windows. Информационно-издательский
дом «Филинъ», М.-1998.-608с.
2.
Боровиков В.П., Боровиков И.П. Statistika
–искусство анализа данных на компьютер. // для профессионалов.-2001.- 656с.
3.
Тюрин
Ю.Н., Макаров А.А. Статистический анализ данных на компьютере / под ред.
В.Э.Фигурнова .М.- 1998.- 528с.
4.
Григорьев
С.Г. Пакет программ statgraphics. С.-П.- 1992 .-104с.
5.
Бюлль
А. Цефель П. SPSS: искусство обработки информации. Анализ статистических
данных и восстановление скрытых закономерностей. 2001.- 608с.
6.
Додж
М., Кината К., Стинсон К. Эффективная работа с Excel 7,0 для windows 95. 1996.- 1040с.
7.
Уокенбах
Д. Библия пользователя Excel 97, 1997.- 624с.