12.Автоматизированные системы управления на производстве

Головицына М.В.

Профессор кафедры РЭУС Александровского филиала Московского Государственного открытого университета им. В.С.Черномырдина, к.т.н.

Формирование исходных данных при построении математических моделей технологических процессов.

Метод компонентного анализа

В работах [1 – 7] автором изложена методика комплексного использования математических методов для построения «сквозных» математических моделей технологических процессов.

Составной частью этой методики является необходимость формирования исходной информации для построения таких моделей.

Поскольку сложный технологический процесс содержит большое количество параметров, имеющих разную физическую природу, то для проведения последующих факторного, корреляционно-регрессионного анализа и др., разработки математических моделей и алгоритмов управления с целью сокращения исходной информации целесообразно проводить выделение групп.

После группировки проводится поиск информативных параметров внутри групп. Для этого используются методы главных компонент и главных факторов.

По методу главных компонент осуществляется представление каждого параметра в виде линейной комбинации «n» некоррелированных переменных (компонент) f_i [8]:

где a_ij - нагрузка j-той компоненты, которая определяется по формуле:

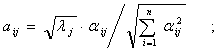
здесь - компоненты собственного вектора матрицы, соответствующего j‑му собственному значению l_j .

Поскольку число компонент равно числу исходных параметров и компоненты некоррелированы, то матрица находится однозначно, а компоненты f₁ ,…, f_n также можно найти через исходные параметры x₁,…,x_n.

Метод главных компонент позволяет упорядочить компоненты по степени их вклада в общую дисперсию, выделить компоненты с большим вкладом в большую дисперсию.

Блок-схема компонентного анализа представлена на рис. 1.

Пояснения к блок-схеме

Начало программы.

Блок 1. Вводятся: N и М - размерности исходной матрицы и матрица.

Блок 2. Вводятся:

МХ - количество переменных, участвующих в анализе (по умолчанию - все);

MFX - максимально допустимое количество компонент (по умолчанию - все);

ЕТА - точность вычислений (по умолчанию - 0.0001);

Q - процент дисперсии, объясняемый главными компонентами (по умолчанию Q = 100%);

IS - задаёт способ стандартизации матрицы ковариаций;

IS = 0 - по среднеквадратичному отклонению (по умолчанию);

IS = 1 - по среднему значению;

IS = 2 - без стандартизации;

IS = -1 - факторный анализ не проводится.

Блок 3. Печатаются исходные данные.

Блок 4. Определяются и печатаются статистические параметры:

ХN - переменная матрица;

SZ - мат.ожидание;

Д - дисперсия;

SQ - стандартное отклонение;

VR - коэффициент вариации.

Блок 5. Определяется коэффициент корреляции A(i,j).

Печатается коэффициент парной корреляции.

Блок 6. Определяется способ стандартизации матрицы.

Стандартизуется матрица корреляции.

Блок 7. Вызывается подпрограмма вычисления собственных векторов.

В массив «В» записываются их значения.

Блок 8. Вычисление сумм и коэффициентов. Вычисление главных компонент.

Вычисление дисперсии и значений компонент.

Блоки 9 и 10. Печать главных компонент.

Осуществляется печать дисперсии главных компонент, выражения компонент через исходные переменные, корреляции компонент с исходными переменными, значений компонент.

Конец программы.

Число факторов определяется из расчёта задаваемого большого вклада (»80-90%) их суммарной дисперсии в суммарную общность. Процесс поиска факторных нагрузок, а затем общностей повторяется итеративно до достижения заданной точности. Следовательно, с известной погрешностью, заранее заданной и удовлетворяющей требованиям исследователя, можно ограничить количество параметров, контролируемых по ходу технологического процесса.

В частности, при исследовании технологического процесса изготовления видеоконтрольного устройства (ВКУ) были получены, например, такие результаты:

Компонентный анализ

Метод главных компонент

	Среднее	Дисперсия	Стандарт
РазВ	2.000312	.001275	.035702
Ампл	3.050000	.043368	.208251
УОтЦ	1.499375	.001212	.034817
УпрИ	1.003021	.001691	.041119
Рсиг	1.994792	.019236	.138693
РазС	.526562	.010419	.102071
ДлИ1	11.693750	.032171	.179363
ДлИ2	1.010417	.026838	.463822
ДлИ3	26.027080	.528311	.726850

Суммарная дисперсия .66452

Вклад переменных в суммарную дисперсию, в %:

РазВ	.1918
Ампл	6.5263
УОтЦ	.1824
УпрИ	.2544
Рсиг	2.8947
РазС	1.5678
ДлИ1	4.8412
ДлИ2	4.0387
ДлИ3	79.5026

Здесь РазВ……. ДлИ3 – параметры технологического процесса изготовления ВКУ.

Очевидно, что эффективность изложенного подхода возрастает при большем количестве исходных параметров процесса.

Литература

1. Головицына М.В. Методология проектирования РЭС. М.: МГОУ. 1993.

2. Головицына М.В. Проектирование автоматизированных технологических комплексов. М.: МГОУ. 2001.

3. Головицына М.В., Агаев И.А., Грозман П.Я. Применение математических методов для сжатия исходной информации при описании технологического процесса выращивания минералов. // Математические методы и АС в геологии. 1988. №12. М.: ЭИ ВИЭМС, 1988. Вып. 11 – 12.

4. Головицына М.В., Пупин А.А., Грозман П.Я. и др. Разработка основ моделирования и принципов построения АСУТП роста монокристаллов. Т.1 с приложениями. Научный отчёт. Гос. Регистрация №01830011460. Александров, 1984.

5. Головицына М.В., Грозман П.Я., Подошва Н.В. Разработка основ моделирования и принципов построения АСУТП роста монокристаллов. Анализ функциональных связей. Т.Т.4 и 5. Научный отчёт №1384 п/с. Гос. Регистрация № 01850003079. Александров, 1985.

6. Головицына М.В. Статистический контроль качества. Методика выбора контрольных точек и контролируемых параметров. «Естественные и технические науки», 2008, №6.

7. Головицына М.В. Предварительная обработка производственной информации: сущность и необходимость. Журнал «Информационные технологии в образовании и науке», 2010. Вып.6. с.103-112.

8. Сажин Ю.В. Комплексное применение статистических методов в исследовании качества продукции. Саратов: Изд-во Саратов. ун-та, 1982.

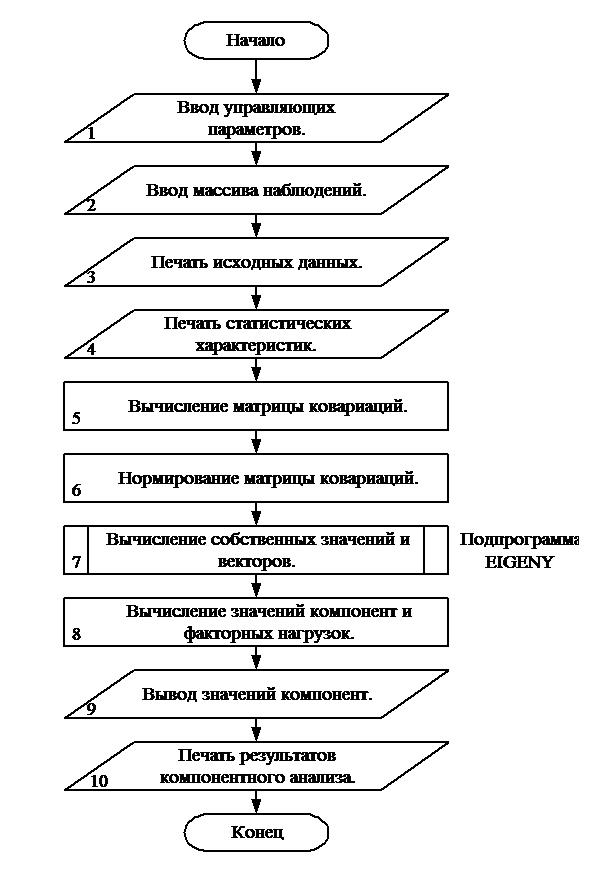
Рис.1. Блок – схема компонентного анализа