Технические науки/ 12.Автоматизированные системы управления на производстве.

Д.т.н. Хвостов А.А., д.т.н. Тихомиров С.Г., к.т.н. Хаустов И.А., к.т.н. Никитченко А.А.

Воронежский государственный университет инженерных технологий, Россия, Военный учебно-научный центр военно-воздушных сил «Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина» (г. Воронеж), Россия

МОДЕЛИРОВАНИЕ ПРОЦЕССА ТЕРМООКИСЛИТЕЛЬНОЙ ДЕСТРУКЦИИ ПОЛИМЕРА МЕТОДОМ МОНТЕ-КАРЛО

Одним из методов прогнозирования свойств эластомеров в процессе их деструкции является имитационное моделирование основных процессов на молекулярном уровне. Причем моделирование поведения отдельных элементарных частей системы дает возможность оценить поведение всей системы на макроуровне в случае, если детерминированная математическая модель неизвестна или неизвестно её решение.

Для имитации процесса термоокислительной деструкции полибутадиена использовалось прямое моделирование методом Монте-Карло. Целью моделирования являлась оценка изменения во времени формы функции молекулярно-массового распределения (ММР) макромолекул в растворе

, (1)

где M – молекулярная масса, dW - массовая доля макромолекул молекулярной массы, лежащей в интервале от М до М + dM.

Каждая макромолекула представлена как массив некоторых абстрактных элементарных частиц, связанных друг с другом жесткой связью (будем считать такую систему частиц моделью макромолекулы). В первом приближении пренебрегаем их подвижностью, массой, взаимодействием, конформационным состоянием и теплообменом. Множество таких идеализированных макромолекул представляет собой выборку из генеральной совокупности всех макромолекул, находящихся в исследуемом объеме.

Качественное соответствие задаваемого на этом этапе состава реальному полимеру осуществляется через функцию ММР. Т.к. в математической идеализации используется распределение количества элементарных моделей макромолекул по их длинам, то в целях экономии вычислительных ресурсов ЭВМ необходимо ввести масштабные коэффициенты, позволяющие ставить в соответствие длины моделей макромолекул весам реальных прототипов, а также концентрации реальных макромолекул в растворе количеству их моделей в исследуемой выборке [1]. Т.о. реализуется отображение и , где и – длина и количество моделей i-ой макромолекулы.

Т.к. процесс деструкции заключается в химическом разрушении связей внутри макромолекул и образовании двух и более новых макромолекул с весами, сумма которых равна весу исходной макромолекулы, то необходимо моделировать элементарный акт разрыва макромолекулярной цепи деструктирующим агентом.

Введем следующие упрощения: 1) считаем, что за один акт взаимодействия осуществляется разрушение одной связи в совокупности всех макромолекул, представленных единым множеством элементарных частиц; 2) место разрыва случайно и подчиняется равномерному закону распределения; 3) за один интервал реального времени осуществляется количество элементарных актов взаимодействия, пропорциональных концентрации деструктора; 4) считаем, что каждый акт взаимодействия соответствует одному интервалу машинного времени.

Представим каждый элементарный акт взаимодействия. Пусть имеется все множество моделей макромолекул L=, являющееся объединением всех множеств элементов, составляющих каждую модель макромолекулы . В результате процесса деструкции выбирается количество точек разрыва , исходя из допущения 3:

(2)

где - концентрация деструктора, D1, D2 – масштабные коэффициенты, k – дискретный эквивалент времени.

Выбор места разрыва выбирается случайным образом в соответствии с равномерным распределением величины порядкового номера элемента множества L в диапазоне от 1 до 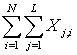. Добавление точки разрыва заключается в определении макромолекулы, подвергшейся деструкции и формировании из неё двух новых моделей макромолекул, являющихся частями исходной. Т.о. каждый акт взаимодействия увеличивает количество моделей макромолекул на одну при сохранении общей длины (суммарной молекулярной массы). При этом вид функции ММР меняется, т.к. весь набор макромолекул теперь состоит из наборов с новыми длинами (молекулярными весами).

Реализация численного эксперимента и его сравнение с данными о изменении ММР полибутадиена в ходе процесса термоокислительной деструкции, полученных с помощью гель-проникающей хроматографии и с помощью разработанной имитационной модели показало качественное соответствие результатов (Рис. 1,2).

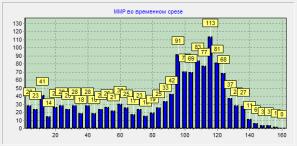
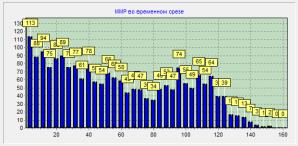
Рис. 1 Результаты имитационного моделирования в начале процесса деструкции и спустя 18 циклов моделирования актов взаимодействия полимера с деструктирующим агентом.

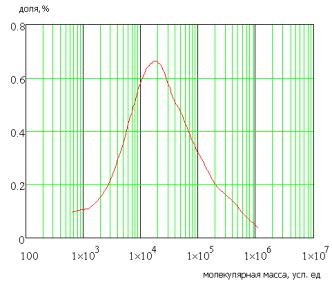
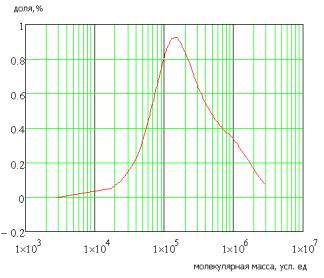
Рис. 2 Результаты хроматографического анализа полимера в начале процесса деструкции и по истечении 1 часа после начала процесса

Анализ результатов показывает, что предлагаемая имитационная модель отражает смещение пика функции ММР и рост концентрации низкомолекулярных фракций, однако не совсем корректно отражает соотношение этих фракций, что говорит о том, что в качестве допущения использовалась равная вероятность деструкции макромолекулы с любой молекулярной массой. Т.о., направлением дальнейшего развития предложенной модели является учет зависимости вероятности взаимодействия макромолекулы с деструктором от её молекулярной массы.

1. Гусев, Ю. К. Имитационное моделирование процесса деструкции полимеров [Текст] / Ю.К. Гусев, С.Г. Тихомиров, А.А. Хвостов, И.А. Хаустов // Вестник ВГТА. – 2012. – №2 – С. 85-88.