Технические науки. Обработка материалов в машиностроении

 

К.т.н. Савелов Д.В., д.т.н. Драгобецкий В.В., Носач А.С.

Кременчугский национальный университет имени Михаила Остроградского, Украина

Исследование способности металлического порошка распределять нагрузку при его взаимодействии с пуансоном вибрационного пресса

 

Для производства изделий из металлических порошков с более высокой плотностью широко используются вибрационные методы. При осуществлении технологического процесса прессования происходит взаимодействие пуансона с металлическим порошком. При этом характер распределения усилия, которое передается от пуансона металлическим частицам порошка, определяет эффективность процесса прессования и качество получаемых изделий.

Предложенные методы описания характера распределения нагрузки в зернистых средах И.И. Кандауровым базируются на том, что взаимодействие отдельных частиц среды представлено в виды так называемой «кирпичной кладки», а прикладываемое усилие распределяется между элементами среды по законам теории вероятностей [1, 2]. Вопросы распределения давлений в прессуемых порошковых телах описаны в трудах М.Ю. Бальшина, Г.М. Жданова [3. 4] и других исследователей, которые в своих работах заложили фундаментальные основы прессования порошковых материалов. Эти исследования базируются на гипотезе о сплошности прессуемого порошкового тела. Данная работа направлена на дополнение и развитие существующих теоретических положений о распределительной способности порошковых сред, находящихся под действием рабочих органов формующих машин. В связи с этим представляет интерес рассмотрение такой модели распределения нагрузки в порошковой смеси, позволяющей в дальнейшем обоснованно представить характер распределения усилия по высоте прорабатываемого слоя порошка.

Целью работы является создание расчетной модели распределения нагрузки в порошке, позволяющей описать характер изменения вибрационной нагрузки в зависимости от толщины прессуемого слоя порошковой смеси.

Металлическая порошковая смесь представляет собой рыхлую сыпучую среду с различной геометрической формой и расположением металлических частиц, обладающих разной твердостью и шероховатостью. Такие тела называют сыпучими или порошковыми [4], поэтому при осуществлении технологического процесса прессования порошковых смесей на вибрационных прессах, где происходит взаимодействие пуансона с порошковой смесью, они обладают способностью распределять внешнюю нагрузку. В работе [4] Г.М. Ждановым при изучении распределяющей способности порошка рассмотрен переход от полупространства к «эквивалентному конусу» бесконечной длины, конфигурация металлических частиц принималась простой, а изменение компонентов напряжений и интенсивности контактной нагрузки учитывается поправочными функциями. 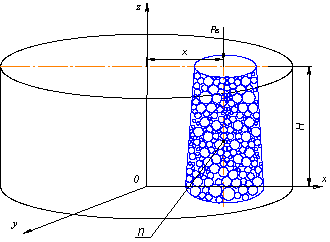Однако же в действительности прессовки в пресс-форме имеют ограниченную высоту . Поэтому для изучения изменения вибрационной нагрузки в порошковой смеси мысленно выделим из всего массива порошковой смеси элемент , находящийся в пресс-форме под давлением прессования и содержащий частицы различной крупности, и рассмотрим его взаимодействие с рабочей поверхностью пуансона вибрационного пресса (рис. 1).

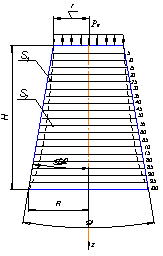
Рисунок 1 – Расчетная схема элемента  порошка для цилиндрической прессовки

Рисунок 2 – Изменение образующих элемента  в зависимости от угла распределения вибрационной нагрузки  и высоты слоя

Теоретические исследования будем проводить для цилиндрического образца. По аналогии с работами [4, 5, 6] элемент  будем рассматривать в полупространстве. Это значит, что элемент  ограничен по высоте и не ограничен по ширине. Поскольку порошковая смесь обладает распределяющей способностью [3 – 6], то естественно предположить, что интенсивность распределения вибрационной нагрузки на поверхности выделенного элемента  будет отличаться от интенсивности нагрузки в основании данного элемента. Будем считать, что характер распределения вибрационной нагрузки в порошковой смеси в направлении прикладываемой нагрузки, будет определяться показателем . Значение показателя  в первом приближении можно определить исходя из следующих соображений. Поскольку порошковая смесь обладает распределяющей способностью, то справедливо предположить, что распределение вибрационной нагрузки между металлическими частицами порошковой смеси имеет форму усеченного конуса с углом при вершине . Основываясь на данных, взятых в работах [5, 6], для проведения теоретических исследований, угол  распределения вибрационной нагрузки в порошковой смеси принят в пределах 150 – 450. По аналогии с рассуждениями, описанными в работах [4, 5, 6], для определения значения показателя  в первом приближении условно представим распределение вибрационной нагрузки между металлическими частицами порошковой смеси в виде усеченного конуса высотой , на вершине которого действует распределенная нагрузка от силы , а нижнее основание радиусом  является площадкой контакта (рис. 2).

В этом случае радиус основания  выделенного элемента  может быть найден из следующей зависимости:

.                                                    (1)

На рис. 2 сплошной линией показано изменение образующих нашего усеченного конуса в зависимости от угла распределения вибрационной нагрузки  и толщины слоя  в направлении вибрационного воздействия. В этом случае площадь рассматриваемого усеченного конуса из порошка может быть найдена из зависимости:

,                                                (2)

где 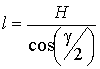 – длина образующей усеченного конуса (рис. 2).

В этом случае выражение для определения площади  примет вид:

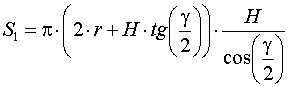,                                    (3)

По аналогии с рассуждениями, приведенными в работах [5, 6], для определения показателя  аппроксимируем выражение (1) зависимостью вида:

.                                                    (4)

В этом случае площадь нашего усеченного конуса может быть найдена по зависимости:

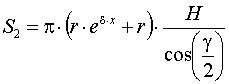.                                      (5)

Приравняем выражения (2) и (5) и, проведя преобразования с учетом того, что , найдем значение показателя  в виде:

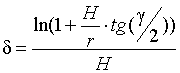.                                           (6)

Полученная зависимость имеет некоторое сходство с зависимостью, полученной в работах [5, 6]. Поэтому следуя аналогичным рассуждениям, определим значение показателя  для крайней точки выделенного усеченного конуса  и, используя зависимость (3) покажем, как будет изменяться образующая усеченного конуса  в полупространстве в зависимости от сечения  слоя порошка  в направлении вибрационного воздействия. В этом случае с учетом того, что ось  принадлежит и полупространству, и усеченному конусу изменение площади усеченного конуса в направлении вибрационного воздействия будет иметь вид, показанный пунктирной линией на рис. 2.

Для уточнения показателя  использовались численные положения метода последовательных приближений и последовательность, описанная в работах [5, 6]. В этом случае площадь нашего усеченного конуса , взаимодействующего с пуансоном вибрационного пресса, может быть представлена в виде:

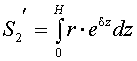,                                                 (7)

откуда, проведя преобразования, найдем:

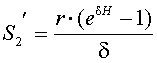.                                               (8)

На рис. 3 показано, как изменяются образующие нашего усеченного конуса по координате  в направлении вибрационного воздействия при определении площади по уточненной зависимости (8).

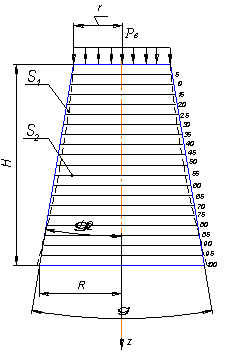
Рисунок 3 – Изменение образующих выделенного усеченного конуса в зависимости от угла распределения вибрационной нагрузки  и толщины слоя  при определении площади  по уточненной зависимости

Анализируя выражение (6) можно сделать вывод, что на числовое значение показателя  влияние оказывает принятый угол распределения вибрационной нагрузки  в порошковой смеси, определяющий положение образующей усеченного конуса, и толщина слоя порошка  в направлении вибрационного воздействия .

По теоретической зависимости (6) было найдено значение показателя  при значениях угла распределения вибрационной нагрузки  от 150 до 450 и толщине слоя порошка в направлении вибрационного воздействия  от 0,005 м до 0,1 м. Для расчета показателя  разработана программа в среде MathCAD 11.

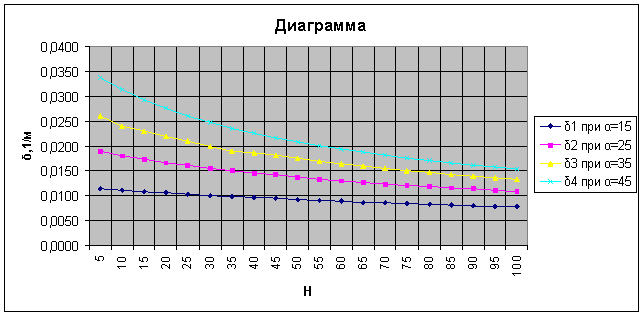
Рисунок 4 – Изменение значений показателя  в зависимости от угла распределения вибрационной нагрузки  и толщины слоя порошка в направлении вибрационного воздействия

На рис. 4 показано, как изменяются числовые значение показателя  в зависимости от угла распределения вибрационной нагрузки  в порошке и высоты усеченного конуса . Анализ полученных графиков позволяет сделать вывод о том, что числовые значения показателя  возрастают при увеличении угла распределения вибрационной нагрузки  в порошке и уменьшается при увеличении высоты слоя усеченного конуса  в направлении вибрационного воздействия.

Выводы. В результате обзора предыдущих теоретических исследований предложена расчетная модель для описания характера изменения вибрационной нагрузки, передаваемой от пуансона вибрационного пресса порошковой смеси в зависимости от толщины слоя порошка.

 

Литература:

1. Порошковая металлургия / С. С. Кипарисов, Г. А. Либенсон. – Москва: Металлургия, – 1980. – 496 с.

2. Кандауров И. И. Механика зернистых сред и её применение в строительстве. 2-е изд., испр. и перераб. Л.: Стройиздат, 1988. – 280с., ил.

3. Бальшин М. Ю. Научные основы порошковой металлургии и металлургия волокна. – Металлургия, 1972. – 264 с.

4. Жданов Г. М. Теория прессования металлических порошков. – Металлургия, 1969. – 336 с.

5. Маслов А.Г., Савелов Д.В. Методика инженерного расчета основных параметров вибрационного рабочего органа грунтопрокалывающей установки. Вісник Кременчуцького державного політехнічного університету: Наукові праці КДПУ, 2004. – Вип.6/2004(29). –С.76-83.

6. Савєлов Д.В. Розробка вібраційного робочого органа грунтопроколюючої установки: автореф. дис. на здобуття наук. ступеня канд. техн. наук: спец. 05.05.04 «Машини для земляних та дорожніх робіт». – Полтава, 2004. – 21 с.