К

К.т.н., доц. Василенко В.С., Дубчак О.В.

Національний авіаційний університет (НАУ), Україна

Циклічність операцій контролю по довільному модулю

Вступ

Нагадаємо, що для контролю чи контролю та поновлення цілісності інформаційних об‘єктів загальної довжини m інформаційних символів, тобто із метою виявлення чи виявлення та виправлення можливих спотворень можна застосувати контроль по деякому модулю [1, 2]. Для цього можна використовувати ділення інформаційного об‘єкту, де − основа системи числення, в якій представлений цей інформаційний об‘єкт, на деякий інший об‘єкт довжиною k символів. Одержаний k символьний лишок тим чи іншим чином дописують до початкового інформаційного об‘єкту. В наслідок цього утворюється так зване базове кодове слово (БКС) довжиною .

Постановка задачі

Таким об‘єктом – контрольним модулем може бути або деяке число (наприклад, число 2 при контролі на парність чи непарність), або більш складна конструкція, наприклад утворюючий поліном (як в циклічних кодах). У першому випадку здійснюється обчислення - значного лишку від розподілу - розрядного початкового інформаційного об‘єкту на відповідний - значний модуль, передавання одержаного - значного БКС каналами передачі, повторне, уже на приймальному боці, обчислення лишку від розподілу інформаційної частини прийнятого БКС та порівняння прийнятого та знов обчисленого лишків. При їх збіганні робиться висновок щодо відсутності спотворень, інакше – про їх наявність та, при певних умовах, − їх корегування.

У другому випадку (наприклад, у циклічних кодах) здійснюється обчислення лишку від розподілу зсунутого на розрядів (чи помноженого на (у відомих циклічних кодах )) початкового інформаційного об‘єкту на утворюючий − значний поліном. Одержаний − значний лишок:

(1)

додається до зсунутого початкового інформаційного об‘єкту, за рахунок чого одержують − значне БКС . На приймальному боці здійснюється обчислення лишку від розподілу одержаного БКС на утворюючий поліном. При цьому одержується лишок:

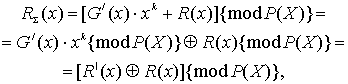(2)

в якому − значення прийнятого БКС із можливою наявністю спотворень в інформаційній частині БКС. У разі відсутності спотворень, тобто при маємо . Тоді у відомих циклічних кодах результат контролю дорівнює нулю , оскільки усі операції додавання здійснюються за модулем 2 (), що позначено вище як , коли f(x) f(x) = 0. В наслідок цього при маємо , що свідчить про відсутність спотворень. В іншому випадку, тобто при наявності спотворень, результат контролю є відмінним від нулю. Неважко упевнитися в тому, що при наявності спотворень не в інформаційній частині БКС, а у надлишкових символах, тобто у разі та одержимо такий же результат .

Відомо, що свою назву цей код одержав за ту властивість, що при контролі циклічно зсунутих БКС одержують ті ж результати, як і без зсуву. Поставимо задачу забезпечення циклічності операцій контролю по довільному модулю.

Циклічність операцій контролю по довільному модулю

Величина − остача від ділення на показує, що, із іншого боку, для одержання цілочисельного результату ділення, а, отже, нульової остачі, досить збільшити ділене на величину:

(3)

Тоді процедура кодування та подальшого виявлення наявності спотворень у вихідному інформаційному слові при використанні запропонованого підходу може полягати в наступній послідовності операцій.

При кодуванні:

1) обчислення остачі за виразом (1):

;

2) доповнення цієї остачі згідно (3) до;

;

3) формування результату завадостійкого кодування у вигляді − значного БКС виду:

. (4)

При декодуванні:

4) здійснення контролю цілісності прийнятого БКС шляхом ділення його на утворюючий поліном та аналізу відповідної остачі.

Тоді в разі відсутності спотворень результат ділення величини на дасть значення, яке дорівнює нулю:

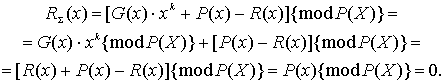(5)

І, навпаки, при слід робити висновок про їх наявність.

Зрозуміло, що процедура (5) є більш тривалою (принаймні на одну операцію) у порівнянні із процедурою (2) і її застосування для звичайних циклічних кодів є не завжди доцільним.

Але при здійсненні контролю із довільним модулем, представленим, наприклад у вигляді деякого простого числа =, автором пропонується застосування процедур і обрахування БКС, і його контролю, які є близькими до процедур кодування звичайним циклічним кодом. При цьому виникає дещо інша ситуація. Зрозуміло, що функції утворюючого поліному повинен перебрати на себе цей контрольний модуль. Тоді доповнення остачі до контрольного модуля набуде вигляду . Подальші операції при застосуванні цього коду покажемо на наступному прикладі.

Приклад 1. Нехай потрібно здійснити кодування деякого інформаційного об‘єкту, наприклад у вигляді десяткового числа 9 (х = 10), по модулю . Оскільки лишок від ділення на такий модуль потребує двох розрядів, то і БКС повинно мати [1, 2] два контрольних розряди (k = 2) і у відповідності із (4) набуде значення:

При відсутності спотворень результат контролю на приймальному боці дасть:

що свідчить про відсутність спотворень. Неважко упевнитися, що при наявності спотворення в одному із символів БКС величина є відмінною від нуля. Наприклад, при одержимо при одержимо і т.п.

Тоді застосування процедури (5) може дати певний виграш у наслідок відсутності, у цьому випадку, необхідності здійснення операції порівняння контрольної ознаки, одержаної разом із БКС, із контрольною ознакою, обрахованою для прийнятого із каналу повідомлення.

На цьому ж прикладі звернемо увагу на можливості щодо циклічності розглянутих операцій контролю по довільному модулю. Ці можливості полягають у вже згаданій властивості, що при контролі циклічно зсунутих БКС одержують ті ж результати, як і без зсуву. Але на відміну від суто двійкових циклічних кодів у разі необхідності контролю циклічно зсунутих БКС слід врахувати обмеження щодо їх контрольних ознак. Ці обмеження зводяться до того, що чисельні значення кодів контрольних ознак, по-перше, не мають бути більшими за контрольний модуль, а, по-друге, повинні бути доповненнями до контрольного модуля. Іншими словами, у разі одержання відмінного від нуля лишка:

1. При наявності впевненості, що контролювалося БКС без зсувів, зробити висновок, що має місце спотворення. При підозрі, що здійснювався контроль циклічно зсунутого БКС слід:

2. Згідно із вище визначеними обмеженнями обрахувати нове значення контрольної ознаки: та здійснити повторний контроль цілісності.

3. У разі одержання лишку, що дорівнює нулю, зробити висновок про відсутність спотворень БКС, яке є циклічно зсунутим. У іншому випадку − висновок, що має місце спотворення.

Приклад 2. Нехай потрібно здійснити декодування інформаційного об‘єкту за прикладом 1, одержаним у вигляді 109 і є підозра, що це БКС може бути циклічно зсунутим.

Контроль цього об‘єкту дасть . Отже, − прийнято спотворене або циклічно зсунуте БКС. Для перевірки щодо останнього припущення із врахуванням того, що у прийнятому БКС у вигляді 109 інформаційна частина дорівнює 1, а контрольна ознака , обрахуємо нове значення контрольної ознаки: та здійснимо повторний контроль цілісності повідомлення 104. Результатом контролю є: . Висновок: прийнятим є неспотворене циклічно зсунуте БКС.

Приклад 3. Нехай потрібно здійснити декодування інформаційного об‘єкту за прикладом 1, одержаним у вигляді 604 і є підозра, що це БКС може бути циклічно зсунутим.

Контроль цього об‘єкту дасть . Для перевірки щодо останнього припущення із врахуванням того, що у прийнятому БКС у вигляді 604 інформаційна частина дорівнює 6, а контрольна ознака , обрахуємо нове значення контрольної ознаки: та здійснимо повторний контроль цілісності повідомлення 609. Результатом контролю є: . Висновок: оскільки підозра щодо циклічного зсуву не підтвердилась, робимо висновок: прийнятим є спотворене БКС.

Таким чином, запропонований підхід свідчить про можливості використання циклічних властивостей певного класу кодів із контролем по довільному модулю.

1 Василенко В.С. Визначення потрібної надлишковості в коді “Зважених груп”. Оптимальна надлишковість. / М.Ю. Василенко, А.В. Чунарьов // Матеріали 6-ої міжнародної науково–практичної конференції “Аktuálni vymoženosti vědy – 2010”, Dĺl 14, 27.06.2010 - 05.07.2010, ст. 22-24.

2 Василенко В.С. Визначення реальної надлишковості для коду "зважених груп". / М.Ю. Василенко, А.В. Чунарьов // Матеріали VІ міжнародної Науково – практичної конференції “Nauka: teoria i praktika – 2010” 07–15 серпня 2010. Nowoczesne informacyjne technologie. Fizyka– Перемишль: “Nauka I studia” 2010. –Т. 7, С. 74–76