УДК 330.46: 519.86

ФРАКТАЛЬНИЙ АНАЛІЗ ХАОТИЧНИХ ЧАСОВИХ РЯДІВ.

Каноненко В.В., к.т.н., доцент, Бех О.В., ст. викладач

Криворізький економічний інститут Київського національного економічного університету ім. Вадима Гетьмана

Мезенцев О.М., аспірант

Київського національного економічного університету ім. Вадима Гетьмана

На основі мінімальних покриттів вводяться нові фрактальні характеристики: розмірність мінімального покриття та індекс фрактальності , тісно пов'язаний з . Для випадку фінансових часових рядів показано, що мінімальний масштаб , необхідний для визначення із прийнятною точністю, на два порядки менше відповідного масштабу для визначення показника Херста H. У роботі показано, що данна функція є індикатором локальної стабільності часового ряду.

Ключові слова: покриття, фрактальні характеристики, індекс фрактальності, фрактальний аналіз, фінансові часові ряди, локальні характеритстики, флуктуації.

Каноненко В. В., Бех А. В., Мезенцев О. М. ФРАКТАЛЬНЫЙ АНАЛИЗ ХАОТИЧЕСКИХ ВРЕМЕННЫХ РЯДОВ / Криворожский экономический институт Киевского национального экономического университета им. Вадима Гетьмана, Украина

На основе минимальных покрытий вводятся новые фрактальные характеристики: размерность минимального покрытия и индекс фрактальности , тесно связанный с . Для случая финансовых временных рядов показано, что минимальный масштаб , необходимый для определения с приемлемой точностью, на два порядка меньше соответствующего масштаба для определения показателя Херста . В работе показано, что данная функция является индикатором локальной стабильности временного ряда.

Ключевые слова: покрытие, фрактальные характеристики, индекс фрактальности, фрактальный анализ, финансовые временные ряди, локальные характеристики, флуктуации.

Kanonenko V.V., Bekh A.V., Mezentsev O.M. FRACTAL ANALYSIS OF THE CHAOTIC TIME SERIES./ Kryvyi Rig Economic Institute of SHEE "Kyiv National Economic University after V. Getman", Ukraine, Kyiv National Economic University after V. Getman, Ukraine

On the basis of the minimal covers we introduce new fractal characteristics: the dimension of minimal covers and the index of fractality related to . For the case of financial series (FS), it is shown that the minimal scale which is necessary for determining with an acceptable accuracy, is two orders smaller than the one for computing the Hurst index . It is in-process rotined that this function is appear the indicator of local stability of time dimention.

Keywords: Time series; Fractal analysis; Scaling; Multifractals; Stock price; Feedback.

ПОСТАНОВКА ЗАДАЧІ

Сучасний фінансовий ринок є ідеальний приклад «природної» складної системи. З одного боку він достатньо хаотичний, оскільки його еволюція визначається волею великої кількості людей, а з іншою в ньому діють стійкі механізми, що визначаються колективною поведінкою учасників. Одним із завдань еконофізики є опис механізмів колективної взаємодії, які можуть привести до виникнення цінової динаміки, подібної спостережуваної на біржі. При цьому вкрай важливим виявляється визначення і опис специфічних властивостей цінових рядів, що відрізняють їх від інших відомих природних процесів. В даний час можна вважати встановленим, що ряди цін є фракталами в широкому діапазоні масштабів (від декількох хвилин, до декількох років) Причому розглядаються достатньо різні часові ряди, що зазвичай породжуються складними нелінійними системами. При цьому встановлено, що, не дивлячись на крайню нерегулярність часових рядів, характер їхньої поведінки залишається незмінним, це пов'язано з тим що вони мають фрактальну структуру і їх поведінка приблизно однакова з точністю до масштабного чинника. Основною характеристикою таких самоподібних структур, як відомо, є розмірність Хаусдорфа для компактної множини в довільному метричному просторі [1].

Якщо в якості апроксимації графіків часових рядів розглядати комплекси, які складаються з двомірних простих фігур (наприклад, кліток), з геометричним чинником , то, як виходить із визначення розмірності Хаусдорфа маємо:

при (1)

де - повна площа комплексу, із масштабом розбиття . Тим часом, на практиці, при спробі обчислити безпосередньо з формули (1), виникає серйозна проблема, яка пов'язана з тим, що, реальні часові ряди завжди мають мінімальний масштаб структури . З цієї причини, для визначення зазвичай розраховують показник Херста (), який для випадкових процесів з Гаусовим законом розподілу, пов'язаний з співвідношенням . Проте для надійного обчислення H потрібний дуже великий репрезентативний масштаб, що містить декілька тисяч даних [2]. Усередині цього масштабу часовий ряд багато раз змінює характер своєї поведінки. Для цього необхідно знайти послідовність апроксимацій, яка давала б достатньо швидкий вихід функції на асимптотичний режим (1).

АНАЛІЗ ОСТАННІХ ДОСЛІДЖЕНЬ

Якийсь час подібні приклади сприймалися математиками як свого роду патології. Проте на початку XIX-го століття їх накопичилося так багато, що виникла потреба в їх класифікації і аналізі. Багато в чому для вирішення цих двох задач у 1919 році Хаусдорф запропонував своє знамените визначення розмірності для компактної множини в довільному метричному просторі. Він відмітив, що у випадку, коли подібні множини покривати кулями з радіусом , то зі зменшенням кількість куль буде зростати за степеневим законом:

(2)

Даний показник Хаусдорф назвав розмірністю. При логарифмуванні обох частин цього виразу і представленні у вигляді рівності для , ми отримаємо точне означення хаусдорфової розмірності :

(3)

Спонукальгим мотивом такої назви стало те, що для звичних у класичному аналізі регулярних множин (наприклад, гладких кривих або поверхонь) збігається з топологічною розмірністю , рівною мінімальному числу координат, необхідних для описання таких множин. Для «патологій» типу килима Серпінського виявилося, що розмірність Хаусдорфа, по-перше, як правило, є дробовим числом, а по-друге, завжди є більшою за топологічну розмірність . Останню властивість пізніше використовував Мандельброт для одного з можливих визначень фрактала, відповідно до якого «фракталом називається множина, для якої » [4].

Для обчислення розмірності модельних фракталів, як виявилося, зручніше використовувати не початкове означення Хаусдорфа, а його модифікацію, основану на властивостях конкретної множини. Для прикладу такої модифікації повернемося до килима Серпінського. Розглянемо уважно килим Серпінського. На першому кроці , а кількість симплексів (зменшених квадратів, із яких складається передфрактал) . На n-м кроці, , а . Переходячи до границі, при , отримаємо: . Неважко показати, що цей результат не зміниться при використанні куль замість симплексів. Але при цьому виникає дуже важливе питання, яке раніше залишалося без належної уваги: «у чому переваги використання передфракталів перед загальним визначенням?» Для відповіді на нього побудуємо в подвійному логарифмічному масштабі функцію для килима Серпінського (див. рис. 1).

Очевидно, що в разі використання передфракталів, всі дані точно ляжуть на цю пряму, починаючи з найбільших . Саме з цієї причини значення фрактальної розмірності килима Серпінського можна отримати вже на першому кроці ітерації. Якщо ж будувати таку залежність для початкового визначення Хаусдорфа, то вийде деяка крива, яка має потрібний нахил тільки в асимптотиці при . Таким чином, використання передфракталів дає в порівнянні із загальним значенням «швидкий вихід на асимптотику». Це відбувається тому, що передфрактали є в деякому сенсі найкращими апроксимаціями початкової множини при фіксованому . Властивість швидкого виходу на асимптотику є особливо

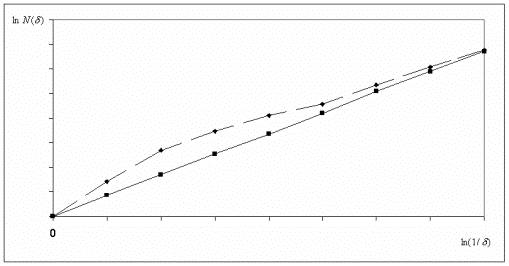
Рис. 1. Залежність для кількості квадратів із стороною передфрактала n-го покоління для килима Серпінського (суцільна лінія) і відповідним чином нормованого мінімального числа куль, радіусу, що покривають килим Серпінського (переривчаста лінія).

важливою для природних фракталів, оскільки при їх аналізі завжди існує мінімальний масштаб структури . Тому відповідний степеневий закон розглядається (докладніше див. [6]) як «проміжна асимптотика» (тобто при береться масштаб малий, у порівнянні з деяким характерним, але багато більше мінімального масштабу ).

ФОРМУЛЮВАННЯ ЦІЛЕЙ

До основних задач дослідження в даній роботі відносяться ідентифікація, прогноз характеристик фінансових часових рядів, цінові ряди акцій, що входять в індекс Доу-Джонса.

У плані ідентифікації буде вирішена задача обгрунтування теоретичного і підтвердження чисельного показника стабільності часового ряду. У плані розвязку задачі прогнозу, буде обгрунтовано теоретично і підтверджено розрахунками ефект збільшення великомасштабних флуктуацій при зменшенні дрібномасштабних. Цей ефект, очевидно, може бути корисним для прогнозу сильних коливань на фінансовому ринку.

Заключним етапом дослідження є побудова алгоритму для розрахунку розмірностей дивних атракторів на основі відносного невеликого числа історичних даних.

МЕТОДИКА ДОСЛІДЖЕННЯ

Як було відмічено вище часові фінансово-економічні ряди мають фрактальну структуру.

Найбільш простим способом дослідження фрактальної структури часових рядів є обчислення їх фрактальної розмірності через клітинну розмірність .

Усередині такого масштабу часовий ряд, як правило, міняє характер своєї поведінки багато раз. Вказаний недолік в рівній мірі властивий і є доцільним способом визначення фрактальної розмірності (наприклад, через кореляційний інтеграл за допомогою алгоритму Грассбергера – Прокаччі [7]). Щоб пов’язати локальну динаміку відповідного процесу з фрактальною розмірністю часового ряду, необхідно визначити розмірність локально з (1).

Нехай на відрізку задана функція , що має не більше скінченого числа точок розриву першого роду: саме такі функції природно розглядати як модельні, наприклад, для фінансових часових рядів. Введемо рівномірне розбиття відрізання

, (4),

де . Покриємо графік цієї функції прямокутниками так, щоб це покриття було мінімальним за площею в класі покриттів прямокутниками з основою (рис. 2). Тоді висота прямокутника на відрізку дорівнюватиме амплітуді, яка є різницею між максимальним та мінімальним значенням функції на цьому відрізку.

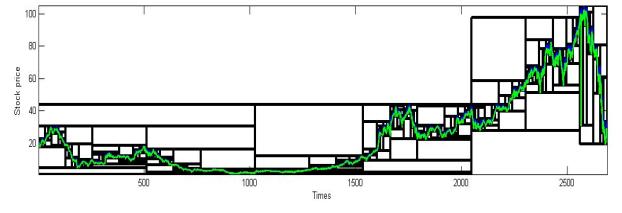
Рис.2. Побудова мінімального покриття. Необхідно розбити область визначення на відрізки завдовжки і покривати графік функції прямокутниками з основою і висотою, яка дорівнює амплітуді коливань функції на даному відрізку. Сірим кольором показані ділянки, що визначають різницю між клітинним і мінімальним покриттям.

Введемо величину:

(5)

Тоді повну площу мінімального покриття можна записати у вигляді:

(6)

Тому з (1) маємо, що

при (7)

де

(8)

Розглянемо з іншими розмірностями і зокрема з клітинною розмірністю , побудуємо клітинне розбиття площини графіка функції як показано на рис. 2. Як що - число кліток, що покривають графік у середині відрізку . Тоді з рис. 2 видно, що

(9)

Згідно формули (9), відмітимо, що оскільки , а також для одномірної функції , маємо . Отже в даному випадку індекс природно назвати індексом фрактальності. Далі при аналізі фінансових часових рядів ми розглядатимемо його як основний фрактальний показник.

АНАЛІЗ ЧАСОВИХ РЯДІВ

Найбільш популярними представниками фрактальних часових функцій є фінансові часові ряди (ряди цін акцій і курсів валют). Існує надійне чисельне підтвердження фрактальної структури таких рядів [8]. Теоретично ж фрактальність зазвичай пов’язують із тим, що для стійкості ринку на ньому мають бути присутніми інвестори з різними інвестиційними горизонтами (від декількох годин до декількох років). Це і призводить до масштабної інваріантності (відсутності виділеного масштабу) цінових рядів на відповідному часовому інтервалі [9]. За допомогою індексу фрактальності нами були досліджені цінові ряди акцій тридцяти компаній, що входять в індекс Доу-Джонса (Dow Jones Industrial Index) з 1970 по 2008 рік. Кожен ряд містить 8145 записів. Кожен запис відповідає одному торговому дню і містить чотири значення: інформацію про мінімальну і максимальну ціну, а також ціни відкриття і закриття.

Для простоти аналізу обмежимося останніми записами для кожної компанії. При обчисленні індексу ми використовували послідовність m вкладених інтервалів (4), де . Кожне розбиття складалося з інтервалів, які мали торгових днів. Для кожного розбиття обчислювалося значення (5). Тут дорівнює різниці між максимальною і мінімальною ціною на інтервалі (зокрема, якщо , то дорівнює різниці між максимальною і мінімальною ціною за день). Типовий приклад поведінки у подвійному логарифмічному масштабі представлений на рис.4 для компанії Microsoft .

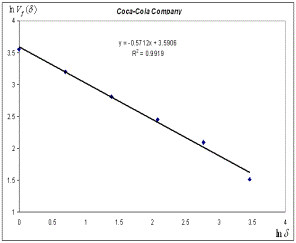
Ми бачимо, що дані майже точно знаходяться на прямій лінії, окрім двох останніх точок, де лінійний режим має злам. Для визначення значення за цими даними слід виключити дві останні точки і знайти лінію регресії за допомогою методу найменших квадратів (МНК). Тоді . При рівні надійності у наведеному прикладі . Де - коефіцієнт детерміації для лінії регресії.

Відзначимо, що для кожної з 30 компаній графік майже точно знаходиться на прямій, також і на всіх менших репрезентативних інтервалах аж до 32-х, а іноді навіть до 16-ти днів. При цьому на інтервалах менших, ніж 500 днів злам лінійної частини графіка як правило зникає. Типовий приклад на інтервалі 32 дні представлений на рис.5 (зліва). При ми отримуємо .

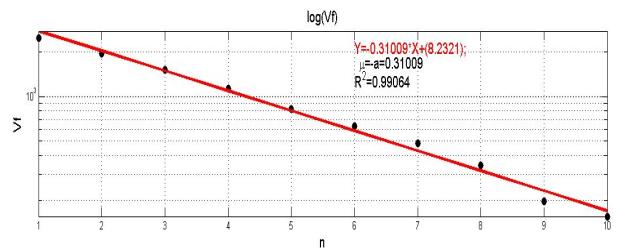
Рис. 3. Залежність у подвійному логарифмічному масштабі для часового ряду поведінки цін компанії Microsoft Corporation, завдовжки 1024 дні. Видно, що точки добре лягають на пряму, починаючи з .

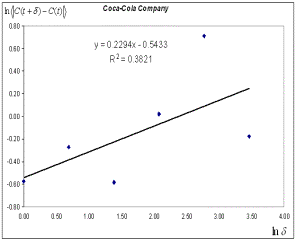
Рис.4. Лог-лог діаграми для чисельного визначення індексу фрактальності (зліва) і показника Херста (справа), на одному і тому ж відрізку фінансового часового ряду, завдовжки 32 дні. Видно, що індекс фрактальності може бути визначений набагато точніше, ніж показник Херста

Щоб оцінити переваги побудованого алгоритму, порівняємо його з методом обчислення фрактальної розмірності за допомогою показника Херста . Для фрактальних часових рядів цей метод традиційно вважається за найбільш ефективний. Як відомо, показник Херста визначається на основі припущення, що

при (13)

де кутові дужки означають усереднювання по часовому інтервалу. Щоб порівняти індекс із показником , розглянемо наступне природне визначення середньої амплітуди на розбитті (див. (3,4)):

(14)

Помножимо (5) на і підставимо у (7). Отримаємо:

при , (15)

де

(17)

Як вже наголошувалося (див. постановку задачі), якщо реалізація гаусівського випадкового процесу, то показник пов’язаний із розмірністю D, а відповідно і з індексом , співвідношенням:

(18)

Отже, в цьому випадку . Проте реальні фінансові ряди, як правило, не є гаусівським і тому значення і можуть сильно відрізнятися. Дійсно, у формулі (15) ми маємо степеневий закон для середньої амплітуди функції на інтервалі довжиною , тоді як у формулі (13) ми маємо степеневий закон для середньої різниці між початковим і кінцевим значенням на тому ж інтервалі. Як виявляється, індекс обчислюється на порядок точніше, ніж показник Херста у переважній більшості випадків. Як типовий приклад на рис. 4 представлені діаграми для визначення і H для одного і того ж ряду представленого на рис. 3. У даному випадку для результати виявилися наступними:

, ,

, .

Як і слід було чекати, індекс визначений набагато точніше, ніж показник .

Таким чином, головною перевагою індексу у порівнянні з іншими фрактальними показниками (зокрема з показником Херста ) є те, що відповідна йому величина має швидкий вихід на степеневий асимптотичний режим. Це дає можливість використовувати його як локальну характеристику, що визначає динаміку початкового процесу, оскільки репрезентативний масштаб, необхідний для надійного визначення індексу , можна вважати як той, що має той же порядок, що і характерний масштаб основних станів процесу. До таких станів належать флети (періоди відносного спокою) і тренди (періоди щодо тривалого руху вгору або вниз). Щоб співставити значення із поведінкою часового ряду, природно ввести функцію як таке значення , яке ще може бути обчислене з прийнятною точністю на мінімальному, попередньому до t інтервалі . У разі неперервного аргументу t за такий інтервал можна було б взяти достатньо малий інтервал. При цьому, оскільки на практиці часовий ряд завжди має мінімальний масштаб (у нашому випадку він дорівнює одному дню), то має кінцеву довжину (у нашому випадку ми беремо = 32 дні).

Як виявляється, використання функції дозволяє істотно просунутися у вирішенні двох основних завдань аналізу часових рядів – завданні ідентифікації і завданні прогнозу.

ФІНАНСОВІ РЯДИ. ІДЕНТИФІКАЦІЯ І ПРОГНОЗ

Завдання ідентифікації зазвичай полягає в коректному визначенні макростану системи на основі спостережуваної реалізації часового ряду. Для вирішення цього завдання стосовно фінансових рядів була розрахована функція для компаній, які входять до складу індексу Доу-Джонса. На рис.5 представлений типовий фрагмент цінового ряду однієї з таких компаній разом з обчисленою для цього фрагмента функцією . [4,5]

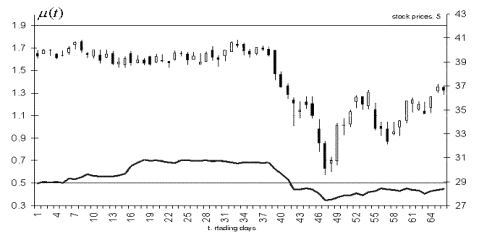
Рис.5. Щоденні ціни акцій компанії Exxon Mobil Corporation (права шкала, японські свічки) і графік функції (ліва шкала, суцільна лінія).

Достатньо перебіжного погляду на рис.6, щоб зрозуміти, що індекс має відношення до поведінки часового ряду. Дійсно, на інтервалі між 1-м і 39-м днем, де ціни поводяться відносно стабільно (флет), . Далі, одночасно з розвитком тренда на графіку цін, різко падає нижче за значення і нарешті після 56-го дня, де ціни знаходяться в проміжному стані між трендом і флетом, повертається до значення . Таким чином, початковий ряд виявляється тим стабільніше, чим більше значення . При цьому, якщо , то спостерігається флет, якщо , спостерігається тренд. Нарешті, якщо , то процес знаходиться в проміжному стані між трендом і флетом.

Нагадаємо, що відповідно до гіпотези «ефективного» ринку (тобто ринку, на якому ціни відображають всю доступну інформацію) поведінка цін має бути близькою до випадкового блукання. Перевірка цього припущення зазвичай зводиться до дослідження розподілу цінових приростів на нормальність і до вивчення їх автокореляційної функції на предмет наявності залежності. Висновки, які можна зробити з подібних досліджень, не дозволяють оцінити ступінь відхилення реальних фінансових рядів від випадкового блукання. Використання функції дозволяє провести докладніший аналіз і зокрема з’ясувати, що часові ряди проводять у стані, близькому до випадкового блукання, менше 30 % загального часу. Використовуючи отримані чисельні дані і вигляд функції (див. рис. 5), можна зробити наступний висновок: реальні часові ряди демонструють складну неперіодичну поведінку, при якій тренди і флети хаотичним чином змінюють броунівський рух. При цьому, знаючи значення функції , можна сказати, який вигляд поведінки переважає в кожній точці ряду [4,5].

Проте найбільш цікавим є використання фрактального аналізу для вирішення завдання прогнозу, яке в загальному випадку полягає у визначенні яких-небудь кількісних або хоча б якісних характеристик майбутньої поведінки тимчасового ряду на базі наявних історичних даних. Виявляється, що наявність степеневої залежності для функції у достатньо широкому діапазоні масштабів дозволяє запропонувати новий підхід до прогнозування фазових переходів у хаотичних системах. Дійсно, звернемося до формул (15, 16) і рис.5. Припустимо, що часовий ряд знаходиться в стані випадкового блукання. У цьому випадку, та залежність описується суцільною лінією на рис.7.

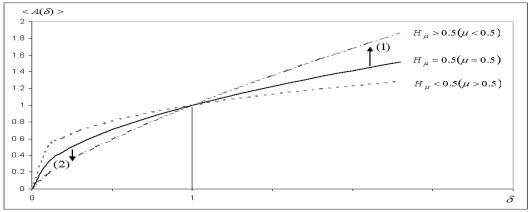
Рис. 6. Залежність для часового ряду при різних значеннях : суцільна лінія відповідає зміні амплітуди для броунівського руху, пунктирна і штрих-пунктирна - для трендів і флетів, відповідно.

Припустимо, що в системі відбувся фазовий перехід, у результаті якого часовий ряд переходить у стан тренда. Це означає, що через деякий час (тобто для великих ) амплітуда коливань збільшиться (стрілка (1) на рис. 6). Але, як видно з графіків, перехід часового ряду в новий стан викличе одночасне зменшення амплітуди коливань на малих масштабах (стрілка (2) на рис. 6). Таким чином, збільшення великомасштабних флуктуацій веде до зменшення дрібномасштабних флуктуацій і навпаки. Цей ефект, який служить ключем до прогнозу сильних флуктуацій на великих масштабах і отримується з наявності степеневого закону, був дійсно виявлений і підтверджений обробкою великої кількості емпіричних даних.

ВИСНОВОК

Підведемо основні підсумки роботи. Для одновимірної фрактальної функції на основі величини (5) ми ввели нові фрактальні показники: індекс фрактальності (7) та розмірність мінімального покриття (8), тісно пов’язану з індексом . Як граничне значення при , збігається зі звичайною фрактальною розмірністю D. Проте в порівнянні з іншими відомими фрактальними показниками алгоритм обчислення розмірності (і відповідно індексу ) має швидкий вихід на степеневий асимптотичний режим для D. Чисельні розрахунки, виконані для цінових рядів акцій компаній, що входять в індекс Доу-Джонса, показали, що репрезентативний масштаб, необхідний для визначення індексу з прийнятною точністю, на два порядки менше, ніж, наприклад, відповідний масштаб для визначення показника Херста . Це дозволяє розглядати індекс як локальний фрактальний показник. Тому для кожного моменту часового ряду ми ввели функцію як значення , розраховане на мінімальному, передньому до інтервалі . Використання цієї функції дозволило нам серйозно просунутися як у плані ідентифікації, так і в плані прогнозу фінансових часових рядів. У плані ідентифікації ми обгрунтували теоретично і підтвердили чисельно на основі достатньої великої кількості емпіричних даних той факт, що індес є показником стабільності часового ряду. Чим більше значення , тим стабільніше ряд. При цьому випадок може бути інтерпретований як тренд, а випадок - як флет. Випадок відповідає броунівському руху. Це дозволило нам за допомогою функції провести тести початкової ціни ряди з тим, щоб виділити в них броунівську компоненту. У плані ж прогнозу обґрунтований теоретично і підтверджений розрахунками ефект збільшення великомасштабних флуктуацій при зменшенні дрібномасштабних. Цей ефект, очевидно, може бути корисним для прогнозу сильних коливань на фінансовому ринку.

Слід відмітити, що побудований локальний фрактальний аналіз можна використовувати також для прогнозу землетрусів [12], ішемічних захворювань [13] і так далі. Однак при розгляді відповідних часових рядів, де кожному значенню аргументу відповідає тільки одне значення функції, ці ряди слід спочатку перетворити на ряди амплітуд, які задані на інтервалах багато більше, ніж «масштаб дозволу» . І, нарешті, слід сказати, що побудований фрактальний аналіз легко узагальнюється, із збереженням усіх своїх переваг, на багатовимірні фрактальні функції (що дуже важливе, наприклад, для теорії розпізнавання образів і теорії стискування зображень). Крім того, за допомогою показника виходить більш адекватний вираз для мультифрактального спектра [10,13]. Нетривіальним є використання побудованого алгоритму для розрахунку розмірностей дивних атракторів на основі відносного невеликого числа історичних даних. Виявляється, що використання такої процедури дозволяє підійти до проблеми прогнозу катастроф абсолютно з іншого боку.

ЛІТЕРАТУРА

1. Зельдович Я.Б. Фракталы. Подобие, промежуточная асимптотика / Я. Б. Зельдович, Д. Д. Соколов // Успехи физических наук.- 1985.- т.146, вып.3. - С. 493-506.

2. Малинецкий Г.Г. Нелинейная динамика: Подходы, результаты, надежды / Малинецкий Г.Г., Потапов А.Б., Подлазов А.В. – М.: КомКнига, 2006. – 280с.

3. Hausdorff F. Dimesion und Ausseres Mass / F. Hausdorff // Matematishe Annalen. — No 79. — 1919. — P. 157–179

4. Dubovikov M.M. Dimension of the minimal cover and fractal analysis of time series / Dubovikov M.M, Starchenko N.S., Dubovikov M.S. // Physica A. - 2004. – V. 339. – P. 591-608.

5. Dubovikov M.M. Variation index and its applications to analysis of fractal structures / Dubovikov M.M., Starchenko N.S. // Sci. Almanac Gordon. - 2003.- № 1. – P. 1-30.

6. Feder J. Fractals / J. Feder. - New York: Plenum Press, 1988. – 261 p.

7. Grassberger P. Characterization of Strange Attractors / Grassberger P., Procaccia I. // Physical Review Letters. – 1983. – V. 50. – P. 346-349.

8. An Introduction to High-Frequency Finance: M. M. Dacorogna, R. Gençay, U. Müller, R. B. Olsen, O. V. Pictet. - San Diego, CA: Academic Press, 2001. - 383 p., ISBN: 0-12-279671-3.

9. Mandelbrot B.B. The Fractal Geometry of Nature / B.B. Mandelbrot. - NewYork: W. H. Freeman, 1982. - 550 p.

10. Pedro Bernaola-Galvan Stanley Scale Invariance in the Nonstationarity of Human Heart Rate / Pedro Bernaola-Galvan, Plamen Ch. Ivanov, Luis A. Nunes Amaral, H. Eugene // Physical Review Letters. – 2001. – V. 87. - № 16. - 4 p.

11. Peters E.E. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics / E.E. Peters. - New York: Wiley, 1994. - 286 p.

12. R. Yulmetyev Possibility between earthquake and explosion seismogram differentiation by discrete stochastic non-Markov processes and local Hurst exponent analysis / R. Yulmetyev, F. Gafarov, P. Hanggi, R. Nigmatullin, S. Kayumov // Physical Review E 64. - 2001. – 14 p.

13. Smith L.A. Lacunarity and intermittency in fluid turbulence / Smith L.A., Fournier J.-D., Spiegel E.A. // Physics Letters A. - 1986. – V. 114. - P. 465-468.