Математика/4.
Математическое моделирование
К.ф.-м.н. Симогин А.А., Симогин Р.А.
Донецкий национальный университет, Украина
Моделирование цены
облигации.
Модель О. Васичека
изменения процентной ставки
1 Введение. Важной задачей
финансовой математики является определение рациональной цены 
, 
, облигации, в условиях изменения процентной ставки 
, 
, во времени, здесь 
— момент погашения
облигации.
Различными
авторами, предложены стохастические модели эволюции процентной ставки. Эти
модели описываются решениями стохастических дифференциальных уравнений [1].
Более подробную информацию относительно этого вопроса можно найти в [2].
В 1977г.
О. Васичек в работе [3] предложил в качестве модели изменения краткосрочной процентной
ставки использовать диффузионный процесс, с постоянной диффузией, который
является решением стохастического дифференциального уравнения Ито:
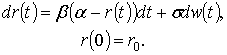(1)
В уравнении (1) 
– долгосрочный средний
уровень процентной ставки, 
– скорость с которой
ставка стремится к этому уровню, 
– постоянный
коэффициент диффузии, 
, 
– стандартный
винеровский процесс, подчиненный потоку 
, 
.
2 Численное моделирование процентной
ставки
При
построении численного решения задачи (1) воспользуемся методом точного
представления решения.
Для уравнения
(1) точным решением является стохастический процесс следующего вида:
, 
. (2)
Введем в
рассмотрение дискретную сетку с узлами в точках 
, здесь 
, 
, 
. Нетрудно видеть, что решение уравнения (1) на сетке 
может быть записано
таким образом:
, (3)
где
, 
,
, 
.
В последнем
выражении
, 
последовательность
независимых случайных величин, имеющих стандартное нормальное распределение.
Построим численное решение уравнения
(1) на сетке 
, используя представление (3). Зафиксируем значения
параметров следующим образом: 
, 
, 
, 
, 
, 
.
Результат моделирования процентной
ставки представлен на рис. 1. На этом рисунке хорошо просматривается общая
тенденция к возрастанию процентной ставки.
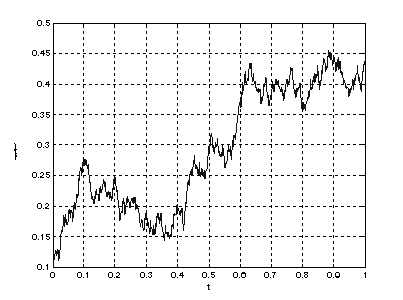
Рис. 1
На рис. 2
представлена средняя эволюция процентной ставки, а так же ее 10-процентная и 90-процентная выборочные квантили.
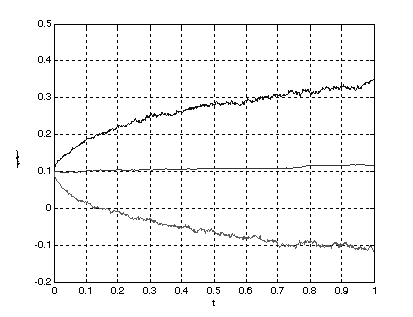
Рис. 2
3 Вычисление
цены облигации посредством метода Монте-Карло. Рассмотрим
дисконтированную бескупонную облигацию, цена которой связана со случайной текущей
процентной ставкой. Эволюция последней, в свою очередь, описывается
стохастическим дифференциальным уравнением (1).
Согласно [2] дисконтированная цена бескупонной
облигации удовлетворяет соотношению
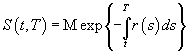
Используя
численное решение уравнения (1), на сетке 
, описанное выражением (3) и метод статистических испытаний,
приблизительно можно считать, что дисконтированная цена равна
,
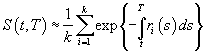здесь
— количество прогонов
модели 
— эволюция процентной
ставки в 
–прогоне.
На рис. 3 изображено изменение
дисконтированной цены облигации в зависимости от времени. Значения параметров
остались неизменными.
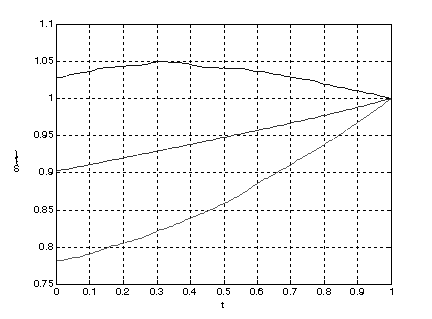
Рис. 3
4. Вывод.
В
данной работе предложена имитационная модель вычисления справедливой цены
облигации в зависимости от срока ее погашения, при этом изменение краткосрочной
процентной ставки описывается моделью О. Васичека. Данный метод позволяет
находить цену облигации и в случае если эволюция изменения процентной ставки
описывается моделью отличной от модели О. Васичека, даже, если аналитическая
формула вычисления цены облигации слишком громоздка или если такой формулы
вообще не существует
ЛИТЕРАТУРА
1. Люу Ю-Д.
Методы и алгоритмы финансовой математики/ Ю-Д. Люу Ю-Д.; Пер. с англ. –М.:БИНОМ.
Лаборатория знаний, 2007. –751с.
2. Ширяев А.Н.
Основы стохастической финансовой математики. Т.1. факты и модели. М.: ФАЗИС,
1998. –512 с.
3. Vasicek O.
An Equilibrium Characterization of the Term Structure // J. Financial
Econom. –1977. Vol. 5. No. 2. –P.177–188.