Ибрагимов У.М., Хамидова Ф.Ф.

Южно-Казахстанский государственный университет им. М.Ауезова

Моделирование задачи фазового перехода

в управляемой системе

 

Постановка задачи. Пусть управляемая система описывается уравнением [1]

                                                               (1)

где , -мерный вектор евклидова пространства  постоянная матрица порядка  управляющий параметр, непустое подмножество пространства . В пространстве  выделено непустое подмножество , которое называется терминальным.

Определение. Будем говорить, что из точки  возможен переход на , если существует измеримая функция , , такая, что решение ,  уравнения

                       ,                                                

при  попадает на , т.е. .

Принцип максимума Понтрягина [2]. Для формулировки принципа максимума мы рассмотрим еще одну систему уравнений относительно допольнительных переменных  

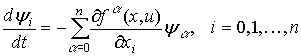.                                     (2)

Вводя  -мерный вектор   и функцию Понтрягина (Гамильтона)

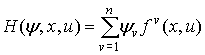,                                                         (3)

мы можем записать уравнения в виде

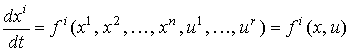,                 (4)

и

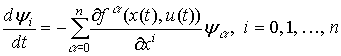                              (5)

в виде гамильтоновой системы

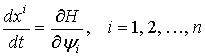,                                                (6)

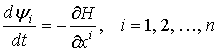.                                   (7)

Теорема [2]. Пусть , - такое допустимое управление, переводящее фазовую точку из положения  в положение , a   - соответствующая траектория, так что . Для оптимальности управления  и траектории  необходимо существование такой ненулевой непрерывной вектор-функции , соответствующей функциями  и , что:

10. для всех , функция  переменного  достигает в точке  максимума

;                                  (8)

20. в конечный момент  выполнено соотношение

.                                                 (9)

Апробация алгоритма и анализ результатов. Рассмотрим уравнени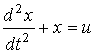е , где  -вещественный управляющий параметр дано в правой части в аддитивной форме подчиненный условию . Приводим уравнения к управляемой системе виду:

 

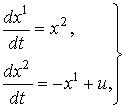                                                       (10)

Рассмотрим задачу о попадании в начало координат (0, 0) из заданного начального состояния . Функция Понтрягина  в рассматриваемом случае имеет вид

.                                           (11)

Далее, для вспомогательных переменных  мы получаем систему уравнений

                                                              

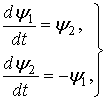
откуда , где  и  -некоторые постоянные.

Для изучения траекторий, соответствующих отрезкам времени, на которых  и , рассмотрим систему

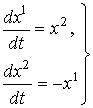                                                             (12)

(получающуюся из системы (10) при ). Произвольное решение этой системы может быть записано в виде

,                     (13)

где  и  -постоянные (). Таким образом, фазовыми траекториями являются окружности с центром в начале координат:

                                                  (14)

Из (13) видно, что движение фазовой точки по окружности (14) совершается по часовой стрелке с линейной скоростью . Отметим, в частности, что за промежуток времени, имеющий длину , фазовая точка двигаясь по часовой стрелке, описывает ровно половину окружности.

Как было указано [2], каждое оптимальное управление  является кусочно-постоянной функцией, получающейся из функции , равной поочередно +1 и -1 на интервалах длины , при помощи сдвига на некоторый отрезок . Если оптимальное управление  поочередно равно +1 и -1 на интервалах , ,  и в заключение, на некотором интервале длины  равно +1, то соответствующая оптимальная траектория может быть построена следующим образом (рис.1).

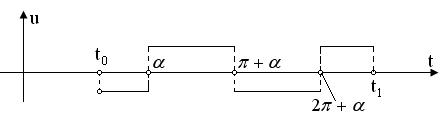
Рисунок 1 - График управления

В течение заключительного отрезка времени фазовая точка движется по окружности (где  на этом отрезке времени), причем по той из этих окружностей, которая проходит через начало координат.

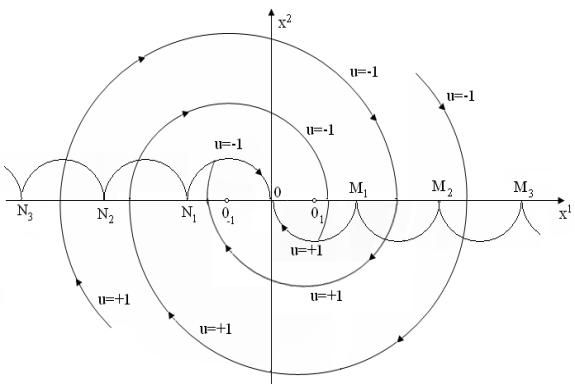
Рисунок 2 – Оптимальные фазовые траектории уравнения

 

Такой окружностью является окружность радиуса 1 с центром в точке  (рис.2). По этой окружности фазовая точка попадает в начало координат, проходя дугу, меньшую половины окружности (где ). Таким образом, обозначив нижнюю полуокружность этой окружности через , мы найдем, что заключительный кусок фазовой траектории представляет собой некоторую дугу  полуокружности .

Выводы. Итак, согласно теореме, только указанные траектории могут быть оптимальными, причем из проведенного исследования видно, что из каждой точки фазовой плоскости исходит только одна траектория, ведущая в начало координат, которая может быть оптимальной. Из теоремы вытекает, что в рассматриваемом примере для любой начальной точки  существует оптимальная траектория. Таким образом, найденные траектории являются оптимальными, и других оптимальных траекторий, ведущих в начало координат, не существует.

 

Литература

  1. Ибрагимов У.М., Оразов И. К задаче оптимального перехода в управляемых линейных системах // Вестник КазНТУ им. К.Сатпаева, -Алматы, №3 (85), 2011. с.203-207
  2. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. –М.: Наука, 1969. -384 с.