Mazhitova A. D.
Mechanical-Mathematical Department, Al-Farabi Kazakh National University,
Al-Farabi ave. 71, Almaty 050038, Kazakhstan;
e-mail: Akmaral.Mazhitova@kaznu.kz
Sub-Riemannian
problem on the three-dimensional
Lie group SOLV –
In this paper we study
geodesics of a left-invariant sub-Riemannian metric on the three-dimensional
solvable Lie group. A system of differential equations for geodesics fined by
Pontryagin maximum principle and by using Hamiltonian structure. In a generic
case the normal geodesics are described by elliptic functions.
Let us consider the three-dimensional Lie group SOLV− formed by all matrices
of the form
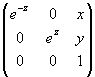 , x, y, z ∈ R. (1)
, x, y, z ∈ R. (1)
Its Lie algebra is spanned by the vectors
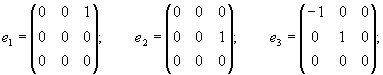
meeting the following commutation relations: ![]() . We take a new basis
. We take a new basis ![]() in which the commutation relations take the form
in which the commutation relations take the form ![]() . Let us consider a left-invariant metric on SOLV−, which is
defined by its values in the unit of the group:
. Let us consider a left-invariant metric on SOLV−, which is
defined by its values in the unit of the group: ![]() . The Lie group SOLV− is diffeomorphic to the space
. The Lie group SOLV− is diffeomorphic to the space ![]() . Indeed,
. Indeed, ![]() are the global coordinates on
SOLV− and they also may be considered as global coordinates on
are the global coordinates on
SOLV− and they also may be considered as global coordinates on ![]() . The tangent space at each point of
SOLV− is spanned by matrices of the form
. The tangent space at each point of
SOLV− is spanned by matrices of the form

which are the left translations of the basic vectors:
![]()
For
the basis ![]() we have
we have![]()
![]() .
.
The inner product takes the form
![]() =
=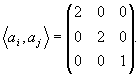 (2)
(2)
In this paper we study the sub-Riemannian problem on the
three-dimensional Lie group SOLV− defined by the two-dimensional
left-invariant distribution ![]() with left-invariant Riemannian metric (2). Geodesics of sub-Riemannian metrics satisfy the
Pontryagin maximum principle (see, for
instance, [5])
with left-invariant Riemannian metric (2). Geodesics of sub-Riemannian metrics satisfy the
Pontryagin maximum principle (see, for
instance, [5])
![]() . (3)
. (3)
The Hamiltonian equations take the form
![]() (4)
(4)
![]()
![]()
The system (3) has three first integrals:
![]()
which are functionally independent almost everywhere, and therefore the system
is completely integrable. Since the flow is left-invariant as well as the
distribution ∆ and the metric, without loss of generality we
assume, that all geodesics originate at
the unit of group, that is, we have the following initial conditions for
the
system (3):
![]() (5)
(5)
In the sequel, we put
![]() .
.
By substituting these expressions into (3), we fine
a expression for pz and by this from third equation of
(4) we obtain
![]() ,
where
,
where ![]() (6)
(6)
The last expression is not integrated in terms
of elementary functions and defines an elliptic integrals, except of special
cases, when this elliptic integral degenerates.
Theorem.
In a generic case the normal
geodesics (with the initial condition (5)) are described by the formulas (for pz
> 0):
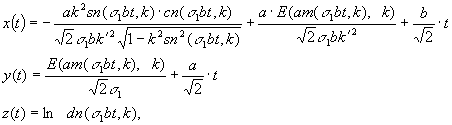
In the degenerated cases the normal geodesics
(with the initial condition (5)) are described in terms of elementary functions
by the formulas
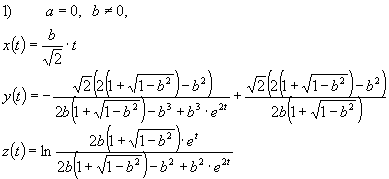
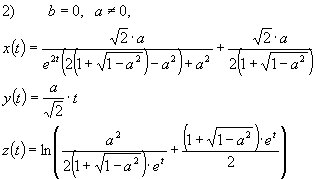
![]() where
where ![]() is
discriminant of subradical expression in
(6)
is
discriminant of subradical expression in
(6)
![]() ;
;
![]() .
.
The qualitative behavior of generic normal geodesic is
quite complicated.
References
1.
Thurston,
W.P. Three-dimensional manifolds, Kleinian groups and hyperbolic geometry.
Bull. Amer. Math. Soc. (N.S.) 1982. V. 6, no.3. P. 357-–381.
2.
Agrachev,
A., and Barilari, D.: Sub-Riemannian structures on 3D Lie groups,
arXiv:1007.4970.
3.
I. Moiseev, Yu. Sachkov, Maxwell strata in
sub-Riemannian problemon the group of motions of a plane, ESAIM: COCV, 16
(2010), 380–399.
4.
Yu. Sachkov,
Conjugate and cut time in the sub-Riemannian problem on the group of motions of
a plane, ESAIM: COCV, 16 (2010), 1018–1039.
5.
Agrachev, A.A., and Sachkov, Yu.L.: Control
theory from the geometric viewpoint. Encyclopaedia of Mathematical Sciences,
87. Control Theory and Optimization, II. Springer-Verlag, Berlin, 2004.
6.
Sachkov,
Yu.L.: Controllability and symmetries of invariant systems on Lie groups and
homogeneous spaces. Fizmatlit, Moscow, 2007. [Russian]
7.
Boscain, U.,
and Rossi, F.: Invariant Carnot-Caratheodory metrics on S3, SO(3),
SL(2), and lens spaces. SIAM J. Control Optim. 47 (2008), 1851–1878.
8.
Calin, O.,
Chang Der-Chen, and Markina, I.: SubRiemannian geometry on the sphere S3.
Canad. J. Math. 61 (2009), 721–739.
9.
Gole, C.,
and Karidi, R.: A note on Carnot geodesics in nilpotent Lie Groups. J. Dynam.
and Control Syst. 1 (1995), 535–549.
10. Gradstein, I.S., and Ryzhik, I.M.: Tables of
Integrals, Series and Products. New York: Academic, 1980.
11. Taimanov, I.A.: Integrable geodesic flows of
non-holonomic metrics, J. Dynam. and Control Syst. 3 (1997), 129–147.
12. Aksenov,
Ye. P, Special Functions in Celestial Mechanics. Nauka, Moscow, 1986. [Russian]