Analysis of Degenerate Solutions to ODEs with Variational Equations of High Order

Victor Varin

Keldysh Institute of Applied Mathematics, Miusskaja square. 4, 125047, Moscow, Russia, varin@keldish.ru

Abstract. We give a definition of variational equations of high order that does not involve infinite dimentional functional
spaces and Frechet derivatives. We use instead formal differentiation on a finite dimentional analytical manifold. This technique is used for an analysis of degenerate solutions on families of periodic solutions. We demonstrate that for any
degenerate solution there exists a non-degenerate system of boundary value problems that allows to compute this solution
with the same accuracy as a generic non-degernerate solution on the family.

Keywords: Degeneracy, variational equations, analytical family.

PACS: 02.30.Hq, 02.30.Oz, 02.30.Xx, 95.10.Ce

Pendulum Type equations with parameters

The neighborhoods of degenerate solutions in ODEs, i.e. local degeneracies, are usually studied with the method of normal forms [1]. To reduce a system of ODEs to its normal form, we need to know the degenerate solution
(a stationary point, a known periodic solution, etc.) in advance. Then, using the normal form of the equations, we can describe solutions in the neighborhood. But there are fairly typical situations in multi-parameter problems when
the degenerate solution is not known, but its existence is obvious. For example, a numerical continuation of a family of solutions by a parameter encounters some problems. It can be a bifurcation with another family, or some topological peculiarity in the family. Such degeneracies are non-local, and, until recently [2], they were computed only with the help of interpolation. We propose a method of computation of such degeneracies with the help of variational equations of higher order. The method is based on treating the solutions to an ODE for all possible values of parameters as some surface or characteristic manifold, included in a finite dimensional Euclidean space. Then each solution to the ODE is a function on the manifold; so the partial derivatives of any order of a solution to the ODE with respect to the local coordinates on the characteristic manifold satisfy variational equations, which are obtained recursively by formal differentiation of the ODE with respect to initial data and parameters. This allows to express the degeneracy in terms of geometry of the characteristic manifold and obtain equations for its computation with the same accuracy as an ordinary solution.

We illustrate this approach on a pendulum type equation that describes oscillations of a satellite on an elliptic orbit, i.e. the Beletsky equation:

(1)

where δ is the double angle between the radius-vector of the mass-center of the satellite; the independent variable ν is the true anomaly of the position of the satellite on the orbit, e is the eccentricity of the orbit; and μ is the inertial parameter. This equation has infinitely many two-parameter families of periodic solutions with various types of degeneracies on them [2].

We define an analytical manifold of all possible solutions to the equation (1) as the following set:

(2)

where δ(0), δ'(0) are initial values of a solution with the fixed parameters e and μ, and δ(π), δ'(π) are computed at ν=π. The first four values in the definition of χ are local coordinates on the manifold.

Each point on the manifold χ corresponds to a unique solution to the equation (1), and the equation itself is a differential identity on the manifold. So we can differentiate this identity with respect to the local coordinates and obtain variational equations of an arbitrary order and in every combination of initial values and parameters.

Let us denote the variations of δ by the letter y, for example:

(3)

Initial values for are and for are . For all other variations initial values are zeros [2].

Degenerate solutions are expressed in a remarkably simple form in terms of variations. The following figure shows some of these solutions at and close to the intersection of three manifolds of periodic solutions to the Beletsky equation. The curve is the intersection of the families of symmetric and asymmetric periodic solutions. This intersection is given by the equation The same equation holds for the curve , where the manifold of the integrable case μ=0 intersects with the manifold of asymmetric solutions. So the point is where three 2-dimentional manifolds intersect. It is given by the equation [2].

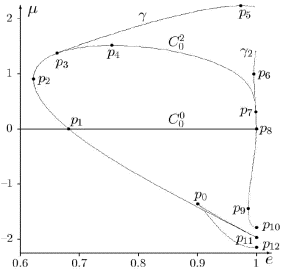
Figure 1. Some degeneracies in the families of symmetric and asymmetric periodic solutions.

Here we can not derive formulas for all the degenerate solutions shown in Fig. 1. Instead, we only describe some of them and refer the reader to the paper [2], where rigorous proofs are given. But we will show how to use this technique on the example of the point corresponding to the Whitney cusp on the family of symmetric periodic solutions.

Extremal points on characteristics are very important, although they are not usually considered as degeneracies. The point on the curve , where the eccentricity attains its extremal value, is given by the equation . The point , where the inertial parameter attains its extremal value, is given by the same equation, but with the substitution of e instead of μ. This is a typical situation with variational equations, when one does not need to derive equations for each degeneracy anew. In fact, the latter equation holds for every similar degenerate solution in similar pendulum type equations, i.e. with two parameters and the same symmetries.

The curve γ in Fig.1 corresponds to the ridge of a symmetric cusp in the family of asymmetric periodic solutions. It is given by the equation Tr=2, where Tr is the trace of the monodromy matrix. The point is where the ridge is
attached to the curve . It given by the equation. This equation also holds for the point , where a similar symmetric cusp originates. Remaining points in Fig. 1, together with their numerical values, see in [2].

Consider the first and the second variations of the equation (1) with respect to the initial value :

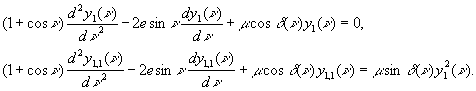(4)

Now we introduce the following system of boundary value problems for the equations (1), (4):

(5)

where k is an iteger.

Theorem. [2] A solution to the system (5) for the unknowns , e, and μ corresponds to the vertex of a Whitney cusp in the family of symmetric generalized periodic solutions to the Beletsky equation with the rotation number k.

In particular, the point satisfies the system (5) for k=0. Note that the vertex of a Whitney cusp is a degeneracy of co-dimension 2, and hence it is an isolated point on the manifold χ. But using this theorem, we can compute these points in various families of periodic solutions tracing them by the parameter k. The following figure shows two analytical curves that satisfy the system (5) for continuous values of k. Bullets in Fig. 2 show the places where k is integer, and so they are the origins of Whitney cusps. Projection of one of such cusp is shown in Fig. 2 for the rotation number k=1.

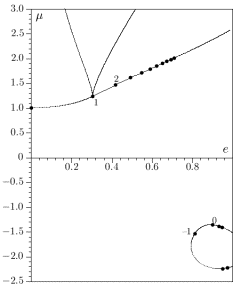
Figure 2. Analitical curves and the vertices of Whitney cusps for integer k.

So variational equations allow to compute non-generic solutions in families of periodic solutions, where ordinary numerical methods fail. To obtain variational equations, we only need to use formal differentiation with respect to initial values and parameters of the problem. These equations form triangular systems of ODEs that can be numerically solved with the same accuracy as the original ODEs. The solutions in the neighborhood of a degenerate solution are represented in a small parameter series whose terms are expressed through variational equations as well.

An application of variational equations for the analysis of degenerate limit cycles see in [3]. In [4], degenerate solutions were computed in the restricted 3-body problem.

Acknowledgments

This work was supported by RFBR grant 11-01-00023.

References

1. A. D. Bruno, Local Methods in Nonlinear Differential Equations , Berlin: Springer-Verlag, 1989.

2. V. P. Varin, “Degeneracies of Periodic Solutions to the Beletsky Equation” in Regular and Chaotic Dynamics, 5, N 3, 2000, pp. 313-328.

3. V. P. Varin, “Poincaré Map for Some Polynomial Systems of Differential Equations” in Sbornik: Mathematics, 195, N 7, 2004, pp. 917-934.

4. A. D. Bruno and V. P. Varin, “Closed Families of Periodic Solutions of a Restricted Three-Body Problem” in Solar System Research, 43, N 3, 2009, pp. 253-276.